wanbo's blog

HackerRank 101Hack 44 is coming
By wanbo, history, 8 years ago, In English

Hello Codeforces community!

I am glad to announce that HackerRank 101 Hack 44 will be held on 13th Dec 2016 at 16:30 UTC. You can sign up for the contest here. Though what's priceless is solving interesting problems and the thrill of competition, prizes make the competition fierce. Top 10 performers will get a HackerRank T-shirt.

The contest will consist of 5 problems with variable scoring distribution. We have tried our best to prepare a nice problem set. Hopefully everyone will enjoy. Also, you'll be able to enjoy the detailed editorials written by the setter.

Good luck and have fun!

  • Vote: I like it
  • +29
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Auto comment: topic has been updated by wanbo (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it +36 Vote: I do not like it

Who's the setter? Is it you?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve C. I came up with a 2D dp solution where dp[i][j]=number of trees having j leaves and a total of i nodes. Then, dp[i][j]=dp[i-1][j]*j + dp[i-1][j-1]*(i-j). Can this recurrence be optimised for 1D?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Even simpler:

    ways(i, j) is the number of ways to choose the numbers from i to j

    solve(i) is the number of possibilities to choose i as a leaf.

    For i to be a leaf you need to choose from 1 to i and from i+1 to n you need have a restriction that you can't choose i, so you can think of this as choosing from i to n-1, so:

    solve(i) = ways(1, i) * ways(i, n-1)

    the expected value will be (solve(2) + solve(3) + ... + solve(n))/ways(1,n)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Yeah, i saw the official editorial and it explains yours approach.Thanks :) I was surprised to see so many successful submissions for this problem. I don't think the idea is so easy to come if you haven't seen something similar.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    Even I wrote a DP solution but TLEd . So I generated the first few numbers of the sequence and tried it in OEIS . It seems it's the order of an Alternating group . Therefore its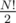 . The final answer is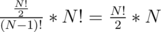

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I started from this: fi is the expected number of leaves in a tree with i nodes (without the factorial part). If we add a new node to a tree, it will increase by one leaf if and only if its parent is an internal node, otherwise it will not change. So we have the formula: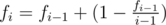

    Let dpi be the result (expected number of leaves multiplied by i!). So dpi = fi * i! After some manipulation, I get this: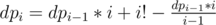

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      I did the same as you taking fi as the expected number of leaves. After deriving the above recurrence, I just checked it's solution on wolfram alpha, which turned out to be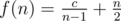 . And f(2) = 1 as per problem. So, the recurrence turned out to be simply 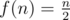. The case of n = 1 was handled separately.

      → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    In problem C. I relize that if we call dp[i] is number of ways to build tree have i leaves then dp[i] will equal to (n-2)C(i-1) = (n-2)!/((i-1)!*(n-i-2)!) but i can't prove it. Can someone help me? Sorry about my bad english !!!

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +54 Vote: I do not like it

Some complaining/advice. I understand that easy problems aren't necessarily interesting but they should be new at least. The first problem looks like it surely appeared on many contests. The third problem also is likely known (I think I've seen it somewhere). I don't say that organizers should know all existing problems but they should think whether it's possible that a problem is new.

Constraints in the second problem are a bit confusing. I think that when someone invented a correct solution, thanks to constraints he/she should know whether it will pass tests. Here it wasn't that obvious that O(n·q) will pass, so maybe a bit lower constraints for q would be better (unless you tried to not allow some slow solutions, but I don't see any except stupidly computing the sieve q times). Anyway, it wasn't an important issue.

And I must say that I enjoyed the last problem a lot. Though, for the 100-th time on HR something was wrong with the scoring. The contest rules say about points for every test, while this problem had binary scoring.

EDIT, one more thing. In the second problem during the contest someone asked "I guess this challenge is basically trying to find how many prime numbers there are between 1 to N. Any hints on how to approach this?". It started a whole discussion about the solution. Please, publish a comment only after a moderator approval. It would make Hackerrank better.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I don't get your point about second problem. There is O(n) solution so it shouldn't be obvious if slower solutions pass.

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

Did the third problem already been given/solved somewhere ? because it took me quite sometime to figure out the series

Triangle of Eulerian numbers

Order of alternating group A_n, or number of even permutations of n letters.

to arrive at solution but people were solving it too quickly or was there an easier out of the box way which i couldn't figure out

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

How to approach DFS edges initially?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Have you read the editorial? To solve the problem, you must understand what is the maximum possible number of forward/back/cross edges for some fixed tree. The editorial explains it a bit.

    what to do later
    → Reply