Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
| Название |
|---|



Can someone explain how to prove a particular greedy approach , like the one given in the editorial for D.
For the D problem I tried a approach of splitting the max(a, b) into blocks of length k and placing the other tea in between them . If I have some more tea bag left I fill them in blocks of k in between the previous one. I got WA in test 9
For example
9 2 5 4
First I get
GGBGGBGNow I fill the remaining 2
Bbefore the firstGso my final output isBBGGBGGBGI haven't read your code, but I guess I can provide a counter-test for your solution. Consider the following test
11 3 6 5. First you getGGGBGGG. After that, you insert remaining fourG's in the beginning. But you can do that, becauseKequals to 3.Sorry , here is my CODE
My output for your test case is
BBBGBGGBGGGLet me attempt a proof at the solution for Problem D:
Let the predicate be that the greedy algorithm will find the solution iff it exists.
Now, how do we know if a solution exists in the first place?
Now, there are 2 cases:
For the first case, it is obvious that the solution exists since we can just take one at a time.
The second case is more tricky. Let us recognise that we need to find a mapping between blocks of tea A and blocks of tea B.
Let tea A be the tea of lesser quantity. Now, in every mapping, we must map at least 1 of A to at most k of B. Hence, |B| can be at most (|A|+1)*k since we can place combine pairs of k Bs and 1 A together. Now, we can place at most k Bs at the right of the last A.
Now that we know how to tell when a valid solution exists, we need to prove our original predicate.
Let's assume that the solution exists based on our above conditions (i.e. there is a valid quantity of B and, we can always find mapping from at least 1 of A to at most n (<=k) of B).
Case 1 is trivial as the greedy algorithm will pick one of each tea in alternating steps.
For case 2,
Let tea A be the tea of lesser quantity, and tea B be the tea of greater quantity.
For case 2, the algorithm will pick at most n (<=k) from tea B (n is maximised). Now, we will pick 1 from tea A since |B| >= |A| at all times. Hence, we have a block mapping from A to B. This choice will repeat until all of A and B have been used up. Note that the choice for A is minimal. Hence, even for a minimum quantity for A, the greedy algorithm will always find the solution.
Now we must prove in the other direction: if the greedy algorithm finds a solution, then the solution exists (is valid).
If the greedy solution finds a solution, then all of the A and B must have been used up since we run the algorithm while |A| > 0 and |B| > 0 and there exists a one to one mapping from each block of A to each block of B.
Hence, the greedy algorithm will find the solution iff it exists.
Do correct me if I am wrong.
Here is an alternate solution for D:
First let us take a as the smaller number and b as the bigger number.
Now for optimal arrangement,we have to arrange it as:
_ a _ a _ a _ a _ and so on. The underscores represent the places where some numbers of b can be placed.
Now we see that the max underscore are (a+1). Therefor maximum b can be (a+1)*k . If b is more than this, than it is not possible.
Now let us first place single b's in the first 'a' underscores.(since b>=a) Then excess amount of b's are (b-a).
Now let us iterate from the first underscore to the last and in every iteration , if there are any excess 'b's left, let us add them to that underscore.(Keep in mind that we cannot add more than k-1 for the first 'a' underscores and k for the last underscore).
Code-23106386
Also use long long instead of int!(My solution in sys tests because of overflow :( )
Thanks a lot I got accepted now.
When you see the constraints and refrain to think more! Unorthodox approach in Problem C. Simulate the entire ride as answer will never be greater than 1e6. :D
Code
how did you gauge that time should only be integers, I planned to simulate but couldn't figure out way to deal with decimal timings
Two cases:
Walking all the way — obviously integer
Walk for a while (t >= 0) then switch to tram, then you could just wait for the tram anyways, as the tram always arrives the destination at the same time regardless of the time of you taking the tram, thus obviously also an integer.
Suppose the tram is coming to pick you up, by walking in the direction of destination are you not cutting down on the time needed? I don't understand why standing at x1 is same as moving in the direction of x2.
Let's consider this simple case where I saw it on a book.
Say Bob is going to school, he could either walk 30 minutes to school, or wait 10 minutes for the bus and reach school in 10 minutes, or you could ride the bus just like in the Tram question we are concerning.
Notice that no matter where you pick up the bus, it's still the SAME BUS. That alone means it is always arriving the school after 20 minutes, as the bus always reaches the destination at a fixed time.
Yeah right, I get it now. Thanks ! Nice Approach.
Легко заметить, что если скорость Игоря выше скорости трамвая, то ответом будет время, за которое Игорь доберется пешком, |x1 - x2|·t2. Но ведь в тесте 5 4 0 1 2 3 1 Скорость (2) Игоря больше, чем скорость трамвая (1), а ответ будет |4-0|*2==8, а в тесте 7
Понятие скорости просто разнится. Эти скорости в обычном понимании (единицы дистанции / время) будут выглядеть как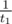 и
и 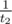 . Подразумевается, что эти величины сравниваются (т.е. условие верно при t1 > t2).
. Подразумевается, что эти величины сравниваются (т.е. условие верно при t1 > t2).
in F, moving the right pointer, if we can fit the song full or partly, we fit the song partly?
i dont think that always works, for example
3 1 10
3 3 8
the pointer would take 3 as a partly song and wont fit 8
but we can make 8 the partly song and listen to the full set
in F, moving the right pointer, if we can fit the song full or partly, we fit the song partly? i dont think that always works, for example 3 1 10 3 3 8 the pointer would take 3 as a partly song and wont fit 8 but we can make 8 the partly song and listen to the full set
also E has weak test cases
for this case:
exist EDIT: checked my solution http://mirror.codeforces.com/contest/746/submission/23099017. it looks like there are some testcases (like tc #6) that are giving different minimum answers, the jury comment says "OK, answer exist"), so does this mean we only need to check for the answer? the problem says minimum amount of changes...
Woah! the checker isn't checking if the answer is minimum or not. This is highly surprising.
I wonder why the author or problem setters are not replying to this query. That means the question statement is wrong? Then the contest should have been unrated :P.
Edit: By trial and error, I have found that number of exchanges need to be <= m to get accepted. So, a simple solution of taking n odds and evens(from set of [1,m] and given numbers) and then fixing already present numbers gets AC.
Oh, it really was a bug in the checker. We are terribly sorry all our checks didn't prevent this. We'll try out best to be even more careful with checkers.
Regarding this problem, we will fix it in the problemset. Thank you for pointing this bug out!
Please explain solution of 746E — Numbers Exchange, from editorial it is not clear..
Let's say we have some pointers for odd number and even number. This pointer is used for which odd/even number we can use next.
First, check each number which has duplicate in original array. If the number has duplicate Change that number in this way : 1.) If the number is odd and the number of odd numbers is more than even numbers, then change that number with next possible even number 2.) If the number is odd and the number of odd numbers is less than or equal to even number, then change that number with next possible odd number (Vice versa if the number is even number)
Then, after change every duplicates, we can have a condition when number of even numbers is different than number of odd numbers. So for every "new array" elements, we check whether if it's odd or even. If it is odd and the number of odd numbers is more than the number of even numbers, we should change it with next possible even number (vice versa with even number in the "new array")
To calculate the number of cards exchange, simply we compare each element in our "newest array" (the one we have after the second "change") with the original array from input.
What case makes it impossible? For every case of changing cards, we check whether our current available odd/even number is more than M.
The checker is not checking for minimum number of exchanges. See Test Case 6
That's interesting. The problem even says to find the minimum number of exchanges.
Please explain problem F. It is not clear from the editorial
Idea: Use two pointers to keep track of the maximum amount of the tracks you can listen if you start from [left for left in range(n)] (find the corresponding right [left, right]).
Say if we have [left, right] already found, it is easy to maintain the sum of decentness while traversing the two pointers, the problem left is how to find the corresponding (right) for each (left). We will use greedy to minimise the listening time, that is to partially listen for the wth longest tracks.
In order to maintain the listening time in a decent time, we should use heaps to keep track of the tracks that are being partially listened and those who are not, and maintain the sum. We should also use two pointers for keeping track of the total listening time — manipulate the heaps and the sum of listening time whenever a track is included / excluded to the current segment.
My solution
How does minimizing the listening time will maximise the total pleasure?
Since you're listening to a continuous segment of the playlist, the more music you listen, the more pleasure you gain (as listening to a music partially does not result in receiving partial pleasantness). You should check if a segment [left, right] can be listened within k seconds, and to achieve that you should compute the minimal time of time required to verify it.
Thanks for your reply.
Actually I wanted to ask how do you decide if a song has to / has not to be listened to ?
However it is indeed correct that since listening to half of the time does not reduce the pleasure we will listen to the maximum length songs for half time only.
// Actually I wanted to ask how do you decide if a song has to / has not to be listened to ?
By the two pointers technique, you fix the left pointer at a place, then you try to extend the right pointer further to the right.
So the iteration will be...
Try to move the right pointer, while doing so, include the songs into our calculation of the total time, and update the answer until we ran out of time or reached the end of the playlist.
Try to move the left pointer, while doing so, exclude the songs from our calculation of the total time, until there's enough time to listen to all of the songs we included, then update the answer.
h1: the heap used for storing songs that are being listened partially
h2: the heap used for storing songs that are being listened fully
Can anyone explain G problem ? It is not clear from the tutorial.
I can, if u stiil need it. And give u even more: another cool solution. But my english is pretty bad :)
First, let's consider the min and max of the amount of "dead-ends".
Note that the amount of dead-ends on each layer is layer-independent — Having more "dead-ends" on the layer above or below doesn't affect the min nor the max of the "dead-ends" that could exist.
Minimum: As we try to avoid "dead-ends" being created, on each node on layer i (1 <= i <= k), we try to allocate at least one node from layer (i+1) as its' child. If layer (i+1) has greater or equal amount of nodes than layer i, then there will be no "dead-ends" as every node gets at least one child. If else, there will be a[i+1] -a[i] "dead-ends" created (where a[x] is the amount of nodes on layer x). The sum of this for each layer will be the min of total "dead-ends"
Maximum: As we try to create as many "dead-ends" as possible, we will allocate all the nodes on layer (i+1) as the child of one single node on layer i, layer i will have a[i] -1 "dead-ends" created. The sum of this for each layer will be the max of total "dead-ends".
Any amount out of this range is impossible to achieve, so we print -1 for those cases.
For any amount x where (min <= x < max), there exist a node u and v such that:
u -> subtree(u)
v -> subtree(v)
where u and v are on the same layer.
To increase the amount of "dead-ends" by one, we can redirect the edges in the following way:
u -> subtree(u), subtree(v)
v is a dead end now.
Therefore we could first construct the tree in the way that creates the least dead-ends, then gradually increase the amount of dead-ends by one until we reach the answer.
My code
Could not understand the logic of D ?
So obviously when a == b, there exists an answer "GBGBGB...". To achieve this state, we will try to reduce abs(a-b). For example, if a > b, then we will first print "GGGGG...B", for each "B", we will print "A" for min(a-b, k) times. If we can reach a == b before b becomes negative, then we have found the answer. Otherwise, since we have tried the best scenario that spams the "G" the most, it is obvious that there does not exist a valid answer for the case.
I hate Problem E.
Can anyone explain problem C?
Claim: min time igor reaches x2 is T=min(igor walk time, tram bypass igor and arrive at x2 time)
Proof: say that igor reaches x2 at time S (S < T). than this means that igor neither walks nor using tram. contradiction! so the claim is right.