Добрый день! Здесь я написал другой разбор задачи "С" с CBR #1
Во первых найдем радиус описанной окружности нашего треугольника, это есть радиус искомого n-угольника. Обозначим радиус описанной окружности через R. Тогда R = abc / 4S, где a, b, c - стороны треугольника, S - площадь треугольника. Найдем все углы етого треугольника и обозначим их как A, B, C. Углы A, B, C можно найти по этой формуле:
A = acos((b2 + c2 - a2) / (2bc))), анологично вычисляются B, C. Теперь найдем n.Находим его вот так: n = pi / gcd(A, B, C). Теперь нам известны R и n, при помощи которых мы можем найти площадь n-угольника по этой формуле: n / 2 * R2 * sin(2pi / n).
Отметим, что gcd(A,B,C) = gcd(gcd(A, B), C)
а функция gcd(x, y) можно вычислить так:
double gcd(double x, double y) {
while (fabs(x) > eps && fabs(y) > eps) {
if (x > y)
x -= floor(x / y) * y;
else
y -= floor(y / x) * x;
}
return x + y;
}
//eps = 1e-4











http://mirror.codeforces.com/blog/entry/85
Единственная проблема - сейчас найти его не так то просто.
http://mirror.codeforces.com/blog/entry/85
Единственная проблема - сейчас найти его не так то просто.
Need the explanation of formula 1. n = pi / gcd(A, B, C) and
2. n ploygon area = n / 2 * R2 * sin(2pi / n)
I couldn't understand The first formula but I understood the second one, The condition in the problem is somewhat like this.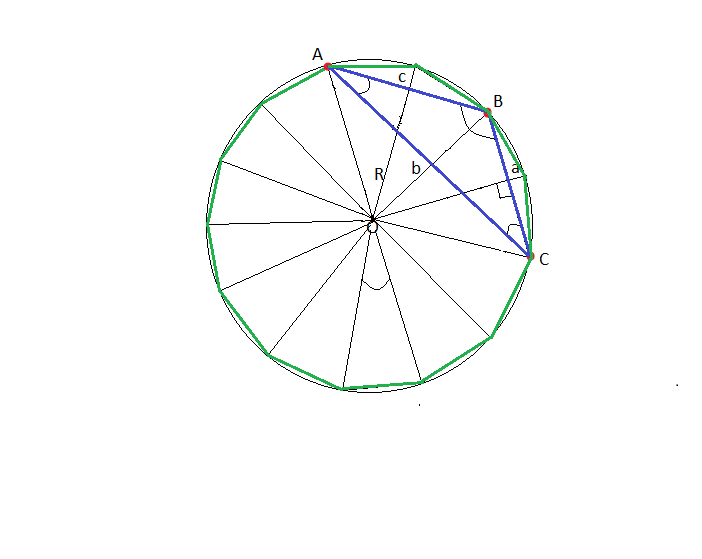 Here we can see that a n sided regular polygon is composed of n triangles all of which have a vertex at the center of the circle. So to find the total area we select one of the triangle's like this and find it's area and multiply it by n.
Here we can see that a n sided regular polygon is composed of n triangles all of which have a vertex at the center of the circle. So to find the total area we select one of the triangle's like this and find it's area and multiply it by n.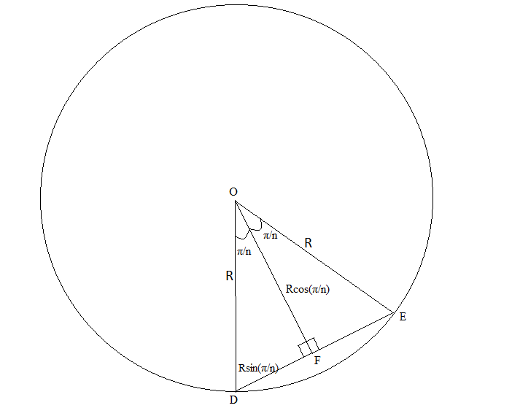 We know the central angle of each such triangle is
We know the central angle of each such triangle is 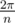 and from the figure we see that OF = (R cos (
and from the figure we see that OF = (R cos ( ))
)) )) also DE = 2Rsin (
)) also DE = 2Rsin ( )
)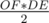 ) =
) =  (R cos (
(R cos ( )) (2Rsin (
)) (2Rsin ( )) = (
)) = (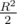 ) sin (
) sin (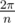 )
)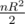 ) sin (
) sin (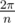 )
)
and DF = (R sin (
So Area of ODE is (
Total area = (
The images were made with MS Paint so I apologize for the quality. I followed whatever the editorial said and got AC 9274841.
.
You should not judge one who made a mistake ( to your mind ) almost 2 years ago. Use time machine !
very easy problem
How do you prove that N = PI / (gcd(A, B, C)) ?
2 * Pi / Nis an angle from the center of the сircumscribed circle between two closest vertices of desired polygon. Then angles from the center between two vertices of triangle will bea * (2 * PI / N),b * (2 * PI / N)andc * (2 * PI / N), wherea + b + c = N. Now let's notice, that the angles of our triangle (A, B, C) are inscribed angles of the сircumscribed circle. ThereforeA = a * (PI / N), etc. Thereforegcd(A, B, C) = PI / N. It is also true ifgcd(a, b, c) > 1, because it is beneficial to take the least N.can someone help me with the concept of epsilon in finding the gcd. Why do most of the accepted answers have it as 10^-4 . when i reduce it to 10^-5 , i get incorrect answer. Can someone tell me how did we decide this value because i think that lesser the value of eps meant a more precise answer??