chill21's blog

What is the best algirithm to find solution of bachet's conjecture ?
By chill21, history, 8 years ago, In English

Any number can be expressed as the sum of squares of four numbers according to lagrange four square theorem, i want to find all possible solution for the given number, I know a algorithm which work in O(n*root(n)), is their any more optimized algorithm ?

thanks in advance :)

  • Vote: I like it
  • +14
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 4   Vote: I like it +2 Vote: I do not like it

The algorithm can be improved to O(N + K), where K is the number of solutions, using meet-in-the-middle.

Build an array A of size N + 1, were A[i] stores a linked-list of all pairs (x, y) with x2 + y2 = i. To do this simply iterate over all pairs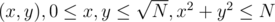 and insert them into A[x2 + y2]. This takes O(N) time overall.

Now we can generate all solutions by iterating with i from 0 to N. For each pair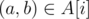 and each pair 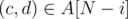, (a, b, c, d) is one solution. This takes O(N + K) time. Some care has to be taken to avoid generating duplicate solutions.

The value of K can be bounded, since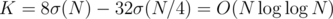 . (See Wikipedia and Wikipedia).

→ Reply