KAN's blog

8VC Venture Cup 2017 — Final Round and Codeforces Round #393 Editorial
By KAN, 8 years ago, In English
Tutorial is loading...

Problem author: KAN.

Tutorial is loading...

Problem author: KAN.

Tutorial is loading...

Problem author: pashka.

Tutorial is loading...

Problem author: pashka.

Tutorial is loading...

Problem author: sivukhin.

Tutorial is loading...

Problem author: Endagorion.

Tutorial is loading...

Problem author: Um_nik.

Tutorial is loading...

Problem author: Um_nik.

  • Vote: I like it
  • +74
  • Vote: I do not like it

Comments Comments (45)
| Write comment?
»
8 years ago, # |
  Vote: I like it +36 Vote: I do not like it

in Div1 D, if O(26*n^2) solutions were intended to pass then time limit is too strict. if only O(n^2) solutions are intended to pass then why did you limit the number of different types to 26?

it's really unfair some people pass with O(26*n^2) solution while the others didn't.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +43 Vote: I do not like it

    I must admit this particular issue didn't get the attention it deserved. I didn't expect a lot of O(kn2) solutions to pass, and I also underestimated the effort needed to optimize to O(n2). In an early stage I considered giving the problem with integers instead of latin letters, but it didn't seem quite elegant. Also, with Ω(n) different symbols allowed the solution would require Ω(n2) memory which is a bit large and may lead to additional time expenses and/or optimizations required, especially if you use a slower/less efficient language.

    As for unfairness, I tend to disagree. If your solution passes the pretests in, say, ~1.5 seconds out of 2, then you know you're in for a sort of gamble and are free to optimize and resubmit (like tourist did). As for the discrepancy between asymptotically identical solutions, well, that can never be completely disposed of. (That said, I don't tend to diminish the oversight on my part.)

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +11 Vote: I do not like it

Another solution for B:

First we give each hobbit on the pillow. Now we distribute pillows to everyone who is close enough to Frodo, until we start giving pillows to all hobbits, or we do not run out of pillows. Create two variables that one of them would take the number of hobbits who needs pillows from left side, the other — from right. If you have not reached the border, increasing the value of the variable. At each step required Left + right + 1 pillow (for Frodo). If you follow the cycle we still have pillows, then add m / n to the answer. Sorry for my English

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    i did the exact same thing...gives me tle on case 6 code

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 6   Vote: I like it +1 Vote: I do not like it

      Your code doesn't implement what Dey suggests. In order to do that with your current code (24051579), you should break the while loop when ptr1 = 1 and ptr2 = n, then add ⌊x / n⌋ to the answer.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    During contest, I also had done exactly the same, only difference was that I didn't break the loop when left = 1 and right = n, that's why I got TLE and I thought that this technique won't work. But your comment help me to get my solution ACCEPTED.

    Thanks..

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Problem D div 1:

Can anyone explain in a little bit more details the formula for the number of reachable strings with comp(...) = u? Why does that equation with number of combinations hold?

UPD Nevermind, got it

→ Reply
»
8 years ago, # |
  Vote: I like it +2 Vote: I do not like it

An alternative O(n2) solution for D that isn't too complicated:

As pointed out in the editorial, observe that a valid string is any string u such that comp(u) is a subsequence of comp(S), where S is the input string. The general idea is to do a dp by "building" all the valid strings (somewhat similar to the classical edit-distance dp).

Define the dp as dpi, j =  number of ways to complete a partially-filled string, where:

  • The partially-filled string has the first i characters determined already
  • The next character we push to the string will correspond to the j-th character in S

Then at each dp state (i, j), we can advance to dp(i + 1, k), for some specific values of k. In particular, these values of k are the first occurrence of each letter in the substring of S from [j, end]. This is because:

  • We include each letter to allow us to skip arbitrary parts of comp(S). This maintains the fact that we are a subsequence.
  • We only use the first occurrence of each letter to prevent double-counting.

The answer is then the sum of all valid dp0, k. The definition of "valid k" is the same as the one above.

A naive implementation of this can run in O(n3). You can optimise this to O(n2) by using a prefix-sum array.

Accepted solution: 24045286

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve problem C if the problem asks for the largest element in the stack after all the operation instead of the top element?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone explain how this formula came in Div2B ((x-1+x-y)y)/2

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +10 Vote: I do not like it

C can also be easily solved with sqrt decomposition. We can create array and store the operations according to their positions. Then we split the whole array into sqrt(N) blocks, and maintain the biggest difference between push() and pop() operations in each block. We only need to change one block after a new query. To find the answer, we can just iterate over the blocks from right to left and find the first block, starting from which the difference is positive.

To understand it better, you can have a look at my code: http://mirror.codeforces.com/contest/759/submission/24052265

→ Reply
»
8 years ago, # |
  Vote: I like it -20 Vote: I do not like it

Problem div1 D can be solved without prefix sums or any other stupid optimization in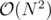 as well. Code

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    congrats for the selection of world finals

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

DIV.2 B Shouldn't the question be "n-1 hobbits are planning to spend the night at Frodo's house" rather than "n hobbits" ???

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yes, you're right. Perhaps he's a hobbit too!

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

756A — Pavel and barbecue and if bi equals 1 then he reverses it. this word show all skewers reverse or one skewer reverse ? l am misunderstand.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If b[i] =  = 1 the skewer at position i will reverse (and then move to position p[i]).

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it -15 Vote: I do not like it

i have a test case for barbeque prob (div2 prob C) 4 2 3 4 2 0 1 0 0

i checked many accepted codes everyone is giving ans as 0 , whereas the ans should be 1 i.e 2 3 4 2 should be 2 3 4 1 can anyone tell me why these codes are accepted ?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Each second Pavel move skewer on position i to position pi  ...

Imagine we have 5 skewers: abcde. What happens with a skewer e when we move skewer a to the place where skewer e is located?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    e would move to a position determined by P.
    Each second the skewers at every i will move to respective Pi. Since P is a permutation, There will always be only one skewer at any i at any time.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      e would move to a position determined by P.

      How is that? If you read statement — Pavel moves skewers (skewers aren't moving by themselves, right?).

      Each second the skewers at every i will move to respective Pi.

      There is no such info in the statement. Instead, the statement says that in one second we move only one skewer. So, according to the statement, after we move a to the position of e, we get the following configuration: abcde ⟶ bcdea.

      Is my reasoning faulted?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        Each second Pavel move skewer on position i to position pi, and if bi equals 1 then he reverses it.
        Since they didnt mention which 'i' will be moved, I interpreted it as he will move all 'i' to their respective pi in one second.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Since they didnt mention which 'i' will be moved

          Can you elaborate a bit — I don't understand this part.

          he will move all 'i' to their respective pi in one second.

          How can he move all skewers in one second if it was explicitly said in the problem description that he moves exactly one skewer in one second? Not 2 skewers, not 3 skewers, but exactly 1 skewer.

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Nevermind, it seems your interpretation is right.
            Back to the original question, e would be in the same position along with the other skewer since they said it's alright if total time can be >=2n which implies repeated positions are fine.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              e would be in the same position along with the other skewer...

              This is also wrong. Here is why.
              Let's assume that we allow for several skewers to be on the same place, i.e. we allow the following configuration:
              ■bcde
              ■■■■a

              Then there is no way for the following sentence to be meaningful:

              Pavel move skewer on position i to position pi

              There are now 2 different skewers in the last position and we don't know which one to choose in order to move it to position pi.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                The choice is yours to make. Basically end goal is to move each skewer to all 2n positions. The order you do it in doesn't matter.

                → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This also had me a little confused. I ended up assuming that after I moved a to e, I immediately started moving e to it's position and so on for all other skewers.

    → Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Can someone please give some more hints on Div1 C?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone tell me in this test case of "Travel card" problem 10 13 45 46 60 103 115 126 150 256 516

Output

20 20 10 0 20 0 0 20 20 10

why ans at trip starting from 60th minute is 20 why it can't be zero

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    it is 0.

    The first line of input contains integer number n (1 ≤ n ≤ 105) — the number of trips made by passenger. So the first number, 10, it's the number of trips

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      can you please tell me trip starting from 115th and 126th minute is why 0?

      → Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can you please tell me trip starting from 115th and 126th minute is why 0?

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can any one please explain analysis to problem E? The above editorial is quite vague. For example,

  • What is the relation/difference between k and pref?

  • What is D? a[pref], a[k], a[n] or a[1]*..*a[n]?

  • "sz is the size of the new layer" -> what is layer? all adjacent ai = 1?

  • What is Di?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    What is the editorial is trying to show is that the state space is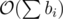 , particularly around 20 times 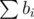, this is because when you are evaluating dp[i][x], i.e. if you are at ith denomination say D, you must have already summed m%D into your sum, because that can not be added to the sum while processing i..n denomination. So, let S be the sum of all denominations from 1..i, so, for this layer( i.e. denomination) valid values of x are only pD + m%D where p varies from 1...S / D. You can see that sum over this S / D is bounded. Correct me if I am wrong.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For Div 1 C, what does the author means when he says "Look at the operations in reverse order"? Is it decreasing p_i or is it the actually the queries we are given in the input, going from bottom to top?

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

There's a very short algorithm for D using O(n2) time and O(kn) space that I haven't seen mentioned. Let a[i] be the number of strings of length i (using the prefix we have processed so far). Let p[c][i] be the value that a[i] had after the last time that character c occurred. For each character c in the string, we update a with the amounts of new strings that end with the character c, which are exactly the strings that ended with a letter other than c (calculated by p[c][i] - a[i] for each length i) appended with any positive number of copies of c. Then we copy a into p[c]. Code

→ Reply
»
8 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

O(log2m) seems to be a little large for m ≤ 1010000 since m ≤ 1010000 seems to be suitable for O(logm(log2(logm)))

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Editorial for div1 B please?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It can be solved using dynamic programming, as we need to find minimum cost for each i th trip, as there are 3 types of tickets so there are 3 ways.

    1. We can buy a ticket for single trip and give 20 rubles (To this we will select the minimum possible cost upto (i-1)th trip.
    2. We can buy a ticket for 90 minutes and give 50 rubles (For this we can cover 90 minutes before the current trip time. For this we can use binary search to find the index which covers this time.)
    3. This case is similar to the 2nd case but here time we can cover is 1440 minutes and cost is 120 rubles.

    As we have to take the minimum cost, so we will take minimum of all these 3 and hence the required ans will be dp[i] — dp[i-1], as we have to give the difference (a-b).

    Refer this submission for more clarity. :)

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Div1C can also be solved in O(mlogm) just using segment tree. (not using lazy propagation)

For segment tree, store sum and maximum suffix sum on each node without reversing the operations.

Updating query takes O(logm) time.

For answering query, make a function find(val, id) which finds the position of rightmost suffix which has suffix sum bigger than 'val' in corresponding node. If right child's maximum suffix sum is bigger than 'val', recursively find answer at right child. Else, recursively find answer at left child, but this time 'val' becomes 'val' — 'right child sum'.

For details, look at AC solution — 29482992

→ Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Insane , that last 2 problems was pure mathematical and can take 1 hr to learn it properly !

→ Reply