mohammedehab2002's blog

Codeforces round #396 editorial
By mohammedehab2002, history, 8 years ago, In English

766A - Mahmoud and Longest Uncommon Subsequence

If the strings are the same, Any subsequence of a is indeed a subsequence of b so the answer is "-1", Otherwise the longer string can't be a subsequence of the other (If they are equal in length and aren't the same, No one can be a subsequence of the other) so the answer is maximum of their lengths.

Code : http://pastebin.com/aJbeTTjw

Time complexity : O(|a| + |b|).

Problem author : me.

Solution author : me.

Testers : me and mahmoudbadawy.

766B - Mahmoud and a Triangle

First solution :-

Let x, y and z be the lengths of 3 line segments such that x ≤ y ≤ z, If they can't form a non-degenerate triangle, Line segments of lengths x - 1, y and z or x, y and z + 1 can't form a non-degenerate triangle, So we don't need to try all the combinations, If we try y as the middle one, We need to try the maximum x that is less than or equal to y and the minimum z that is greater than or equal to y, The easiest way to do so is to sort the line segments and try every consecutive 3.

Code : http://pastebin.com/NsCkbQFS

Time complexity : O(nlog(n)).

Second solution :-

Depending on the note from the first solution, If we try to generate a sequence such that after sorting, Every consecutive 3 line segments will form a degenerate triangle, It will be 1 1 2 3 5 8 13 ... which is Fibonacci sequence, Fibonacci is a fast growing sequence, fib(45) = 1134903170, Notice that Fibonacci makes maximum n with "NO" as the answer, That means the answer is indeed "YES" for n ≥ 45, For n < 45, You can do the naive O(n3) solution or the first solution.

Code : http://pastebin.com/82XcJfgp

Let x be the number that satisfies these inequalities:-

fib(x) ≤ maxAi.

fib(x + 1) > maxAi.

Time complexity : O(x3) or O(xlog(x)).

Problem author : me.

Solutions author : me.

Testers : me and mahmoudbadawy.

766C - Mahmoud and a Message

Let dp[i] be the number of ways to split the prefix of s ending at index i into substrings that fulfills the conditions. Let it be 1-indexed. Our base case is dp[0] = 1. Our answer is dp[n]. Now let's calculate it for every i. Let l be the minimum possible index such that the substring from l to i satisfies the condition, Let x be a moving pointer, At the beginning x = i - 1 and it decreases, Every time we decrease x, We calculate the new value of l depending on the current character like that, l = max(l, i - as[x]). While x is greater than or equal to l we add dp[x] to dp[i], To find the longest substring, Find maximum i - x, To find the minimum number of substrings, there is an easy greedy solution, Find the longest valid prefix and delete it and do the same again until the string is empty, The number of times this operation is repeated is our answer, Or see the dynamic programming solution in the code.

Code : http://pastebin.com/4JiXSwfU

Time complexity : O(n2).

Try to find an O(n) solution(I'll post a hard version of some problems on this blog soon).

Problem authors : me and mahmoudbadawy.

Solution authors : me and mahmoudbadawy.

Testers : me and mahmoudbadawy.

766D - Mahmoud and a Dictionary

Let's build a graph containing the words, For every relation in the input add a new edge with the weight of 0 if they are equal and 1 if they are opposites, If adding the edge doesn't make the graph cyclic, Our relation is valid, Otherwise it may be valid or invalid so we'll answer them offline. Check if adding that edge will make the graph cyclic or not using union-find like Kruskal's algorithm. Suspend answering relations that will make the graph cyclic, Now we have a forest of trees, Let cum[i] be the xor of the weights on the edges in the path from the root of the component of node i to node i. Calculate it using dfs. To find the relation between 2 words u and v, Check if they are in the same component using union-find, If they aren't, The answer is 3 otherwise the answer is 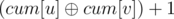, Now to answer suspended relations, Find the relation between the 2 words and check if it's the same as the input relation, Then answer the queries.

Code : http://pastebin.com/WqwduaYs

Time complexity : O((n + m + q)log(n) * maxL) where maxL is the length of the longest string considering that union-find works in constant time.

Problem author : mahmoudbadawy.

Solution author : me.

Testers : me and mahmoudbadawy.

Wait for a hard version of this problem.

766E - Mahmoud and a xor trip

If we have an array ans[i] which represents the number of paths that makes the ith bit sit to 1, Our answer will be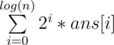

Let arr[i][x] be the binary value of the xth bit of the number attached to node i(just to make work easier).

There are 2 types of paths from node u to node v where u is less in depth than or equal to v, Paths going down which are paths with lca(u, v)=u and other paths, Let's root the tree at node 1 and dfs, let current node be node, Let dp[i][x][j] be the number of paths going down from node i that makes the xth bit's value equal to j. A path going down from node i is a path going down from a child of i with node i concatenated to it so let's calculate our dp. A path that isn't going down is a concatenation of 2 paths which are going down from lca(u, v), Now we can calculate ans. See the code for formulas.

Code : http://pastebin.com/n2a3kijD

Time complexity : O(nlog(ai)).

Problem author : me.

Solution author : me.

Tester : mahmoudbadawy.

  • Vote: I like it
  • +103
  • Vote: I do not like it

Comments Comments (75)
| Write comment?
»
8 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Auto comment: topic has been updated by mohammedehab2002 (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Thanks for really fast editorial.

→ Reply
»
8 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Waiting for O(N) solution for C

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    It's just the same thing again. maintain prefix sums on dp and use a two pointer approach to find the minimum index where we can split.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +2 Vote: I do not like it

      Or, Maintain another dp such that dp[i][x] is the last index less than or equal to i such that character x appears, You can calculate l in O(1) with that dp and the sum in O(1) with a cumulative.

      → Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Very fast editorials...Thanks alot :-)

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

Problem C O(N) solution hint: You can use two pointers with monotonic queue range minimum and partial sums.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    Or just keep a boolean array of size 26, indicating the presence of each letter in the current segment. :p

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      This will be O(N * Σ) where Σ is the alphabet size :P

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        As the alphabet size is considerate to be constant (in this task) the complexity is O(N)

        → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I should know min(v[j]), l<=j<=I, where l is my current left pointer, i is the current index. How do i get it in O(1)?

    → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I tried to solve this question with the matrix multiplication method but getting a timeout. I have only just implemented a partial solution that calculates no of ways to split. Can you help me? Here is my solution...

    typedef long long ll;

    using namespace std;

    ll n;

    string str;

    map <char,ll> m;

    ll solve(ll l, ll r) { if (l>r) { //cout<<"l>r "<<l<<" "<<r<<endl; return 0; }

    ll min=LLONG_MAX;

ll tot=0;

for (ll i=l;i<=r;i++)
{
    //cout<<l<<" "<<i<<endl;
    min=min<m[str[i]]?min:m[str[i]];

    ll len=i-l+1;

    if (len>min)   break;

    if (i==r)
    {
       tot++;
       break;
    }

    tot=(tot+solve(i+1,r))%MOD;
    //cout<<l<<" "<<i<<" "<<tot<<endl;
}

return tot;

    }

    int main() { cin>>n;

    cin>>str;

for (ll i=0;i<26;i++)
{
    ll a;
    cin>>a;

    m['a'+i]=a;
}

ll tot=solve(0,n-1);

cout<<tot<<endl;

    }

    Thnx in advance...

    → Reply
»
8 years ago, # |
  Vote: I like it +10 Vote: I do not like it

We can do D using dsu which works online

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I though the same. Can you help me? I got MLE, and I don't know why... Here is my code: http://mirror.codeforces.com/contest/766/submission/24508577

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you explain how?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +20 Vote: I do not like it

      Cleaned my ugly dsu solution and made it pretty: 24513551

      My idea was the following. For each set the representative of the set stores the index of a value of the opposite set (or -1 if it has no opposite). When combining two sets x and y, you additionally have to union the sets opposite(x) and opposite(y) and set the opposite links afterwards. And when you want to make the sets x and y opposite, you have to union the sets x and opposite(y) and the sets opposite(x) and y and also set the opposite links new.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it +3 Vote: I do not like it

        Thanks for the idea. It was quite time consuming to get everything right with the code.

        Anybody who's still struggling, here's further explanation —

        1. synonyms must be in the same tree of the dsu structure. There can be many dsu trees. The whole input will represent a dsu forest.

        2. only the representative element of a particular dsu tree will hold information about the antonym tree's representative element. and that antonym tree's rep. element will hold information about the former tree's representative elements.

        3. the antonym value of each dictionary string will be = "none" (I used -1, because "none" can be in the dictionary) if it's not the rep. element of it's own tree.(this was important in my implementation, otherwise, there will be too many pointers between trees and they can't be tracked to the values we need)

        4. the antonym value of rep. elements which don't have an antonym yet will also have antonym set to none.

        5. to summarize,

        the forest will have multiple dsu trees, and a few undirected antonym edges, such that each tree is associated with at most one antonym edge.

        if a particular tree has more than one antonym edge( from rep. element only, as other vertices of a tree have antonym value set to null ) then each antonym tree of this particular tree can be joined into a single tree, therefore restoring the "each tree has at most one antonym edge" property.

        We must now appropriately set some antonym values to "none", after joining the antonym trees, and make sure that the antonym edge that still remains points both ways.

        1. dsu trees can be formed as map< string, string >. antonym edges can also be represented as map< string, string >. took 3100ms.
        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I did it and it doesn't work. http://mirror.codeforces.com/contest/766/submission/24809940 No matter what I do it won't pass test 10.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          Here's a minimal test case that doesn't work:

          2 2 0
A B
2 A B
2 A B
          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            Thanks, here is my newest and clearest version and it passes this minimal test case, but not test 10. I really can't find the error here. http://mirror.codeforces.com/contest/766/submission/24810822

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
                Vote: I like it +1 Vote: I do not like it

              Try this test:

              5 4 1
A B C D E
1 C E
2 A C
2 B D
2 A B
A D

              The error happens during the input 2 A B in the following code: 

                  unio(b, find_ant(a));
    a = find_par(a);
    b = find_par(b);
    unio(a, find_ant(b));
    a = find_par(a);
    b = find_par(b);
    ant[a] = b;
    ant[b] = a;

              a = "A" and b = "B". In the first line you union "B" and find_ant("A") = "C". "C" gets the new parent of the combined set. Then you update a and b to their parents, so b becomes "C". But by doing this, you lost the information that "B" is an antonymy of "D". So the "A" and "D" don't get unioned.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                Thank you so much, you really helped me a lot. I spent hours trying to find the mistake. How did you find it? Did you look into the code or did you find a counterexample?

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  8 years ago, # ^ |
                    Vote: I like it +1 Vote: I do not like it

                  Mostly by looking at the code and trying some examples on paper. But it also took me quite a while to find the error.

                  → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      You always keep words that are equal in the same set. Furthermore for every word you keep a reference to a word of the antonymy set if it exists.

      At the start every word is in its own set and does not have an antonymy. When adding a synonym you check if the antonym of one word is in the same set as the other word. (Then this relation is invalid). Otherwise you use Union to put them in the same set. You also have to join the antonyms of the words. When adding a antonym you check if both words are in the same set, then the relatioin is invalid. Otherwise you join the antonym of word a with the set of word b and vice versa.

      I think I may have done some redundant stuff, but it works: http://mirror.codeforces.com/contest/766/submission/24510075

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    yep! 24703668

    I used some of the ideas shown here but here are my drawings of all online cases

    sorry I didn't put when to mark the solution as invalid, In my code it is shown.

    I hope my image helps somebody to reason this approach.

    → Reply
»
8 years ago, # |
  Vote: I like it +87 Vote: I do not like it

Let cum[i] be the xor of the weights on the edges in the path from the root of...

Variable naming is awesome.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

Tried to implement C during contest in O(N3), but couldn't finish debugging. O(N3) passed system tests, indeed 24514033.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could someone explain why the dp (for the number of ways) works for C? I can't seem to understand why the base case is 1 or why we add dp[x] when x is also equal to L.

Like for the first sample case when the string is "aab" and we get to letter b, L would end up equaling 1 (since i = 3 and a1 = 2) but why would we add the dp value at position 1 if the letter at position one can't be in the same substring as position 3?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    did not get that too..confusing explanation

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    My DP solution is a little different. It is easy to dinamically calculate two functions: 1) f(i,j) = number of ways to split first i symbols of our string where rightmost word has length j, 2) g(i,j) = minimal number of words in splits of first i symbols of our string where rightmost word has length j. I can write recurrent equations if needed.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Interesting. I think I'll try and figure out the recurrent equations and probably solve this problem 2 ways. Thanks for the help!

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hey ! Yeah it seems a bit confusing but you can approach it like this as well ,

    let dp[i] = number of partitions possible if the last string ends at index i .

    for this you have to check for every substring ending at index i and check if it is a valid one .Let the string be j.....i .

    If it is valid simply add dp[j-1] to dp[i] .i.e these much partitions can be made by having last string as s[j.....i] .

    Coming to the base case :

    You can have it as :

    dp[0] = 1 where 0 indicates the first letter of the given string as there is only one way to split a single character .i.e the character itself.

    and dp[n-1] will be the answer .

    Can refer my submission : link

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you so much! This makes a lot more sense to me.

      → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Hi, for the question C,

For the first example test case, how come that "aab" (the whole string) can't be included into the number of possible ways?

Because from my understanding, the limit of a=2 and b=3 doesn't apply to the "aab" thus we can include it into the possible ways.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    yes, we can include it. The solution splittings are — {a,a,b}, {a, ab}, {aa, b}

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      Why does {aab} don't get included into the splitting?

      Because from the limit rules it said a1=2 and a2=3, but from {aab} it only has a=2 & b=1, so it's totally possible to include it into the splitting.

      edit*: I assuming that a1 = limit of char A, a2 = limit of char B. Is my understanding is wrong?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It's wrong .. a1 = limit of the string size that we can write char A in it .. read the announcement about the problem B

        → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I assumed the same during contest but it is wrong.

    That's because this magical paper doesn't allow character number i in the English alphabet to be written on it in a string of length more than ai.

    It means character i cannot be present in a substring of length more than ai.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      OMG, this question really gives me a hard time to think. :(

      I think maybe that I got confuse or not understand those text (your marked text) completely.

      So, from the test case, we have a1=2 and a2=3, which means that the maximum of character 'a' and 'b' is both 2 and 3 respectively.

      Thus, "aaa" isn't possible because it has three 'a's. The question said the maximum is a1=2, thus it's not possible.

      Another example might be, "bbbb", also is not possible because it has four "b"s. The question said the maximum is a2=3, thus it's not possible.

      Then why for "aab" it can't be included inside the splitting? I ask that because it only has a=2 and b=1, which totally fine with the rule a1=2 and a2=3.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        That's because this magical paper doesn't allow character number i in the English alphabet to be written on it in a string of length more than ai.

        Suppose there is 'a' present in string then length of that string cannot be more than a[0].

        Notice length NOT frequency!

        So "aab" is not accepted because length of string is more than 2 but a[0]=2.

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        I think you misunderstood the problem.

        Limit given for each characters is the max length of substring character can be a part of.

        so if we include "aab" as one possible way then it violate the condition that a1 = 2 i.e 'a' cannot be part of substring more than length 2 (in case of "aab" length is 3)

        I hope this helps.

        → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Добрый день. Кто может написать решение 3 задачи нормальным русским языком? Заранее спасибо.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +9 Vote: I do not like it

    Задача А:

    Задача А

    Задача В

    Задача В

    Задача С.

    Задача С
    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Who knows features of Test 27 on problem D? For some reason my solution (Python) have an RE on it... Using onlene dsu like in this comment.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can anyone explain why my code fails on testcase 10 problem D Code Is the problem hashing collision?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Where does log(n) come from in the described solution for D? Assuming dsu works in constant time it takes linear time to construct the graph andlinear time to run 1 dfs, which is also linear, and then we do m+n queries at O(1). Have I missed anything?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

When I had read the problem E,I wrote a code using Centroid Decomposition without thinking twice....

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It's been 3 years though, but if you can read the statement again, and help with, how to approach this with centroid decomposition? . Thanks

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I also solved this with centroid decomposition. For each centroid I calculate the sum of xors of paths going through the centroid (including the path with the centorid alone).

      I have two arrays curCount[32][2] and allCount[32][2]. I do dfs of all the subtrees from the centroid. In this dfs I keep track of the xor down the dfs and in curCount I keep the total amount of ones and zeros at each bit position.

      After the dfs I go through curCount and update the answer for this centroid. (at bit i check how many paths will have xor of 1 with the root, and xor of 1 with previous paths)

      Finally I update the allCount with curCount, and reset curCount to 1.

      I hope this helps, if you want to see my code feel free to ask! :)

      → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

As a Chinese participant, I was surprised to find that 766D is very similar to a problem Food Chain in China National Olympiad in Informatics in 2006....

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain Problem E in detail ???? .Particularly how do we come to such DP states and the transiton between the states .Thanks in advance :)

→ Reply
»
8 years ago, # |
  Vote: I like it +6 Vote: I do not like it

D becomes much simpler if while merging we copy each element of smaller set to larger set and change their color accordingly.Not faster, but easier to code.

The number of times we have to push an element in a larger set is at max logN time, because whenever we push a smaller set to larger set the size of smaller set becomes atleast double.How manny times can a set size becomes double? Log2(N). So Complexity is N*logN.

That's why DSU with only Union by rank has time complexity of N*LogN ,But when we do path compression along with Union by rank the amortized complexity becomes O(K*N) where K<=6 for practical values of N.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

A nice solution for problem B(div.2) with random!! ;) Code: 24497457 The exception value is really good=)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please explain second solution of problem B, Mahmoud and Triangles

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    for a non-degenerate triangle(non-zero area) we have to satisfy the condition x+y>z. If we sort the length in increasing order, we only have to check for three consecutive lengths to be the sides of triangle (i-1, i, i+1) and check if(a[i+1]<(a[i]+a[i-1])).

    If this condition is false for i-1, i, i+1 sides it will be false for any triples where largest sides is greater than i+1th value. Similarly we take i-1th side as smaller side if the condition is false to i-1, i, i+1 it will be false to any value smaller than i-1th side length.

    So, in the best case for an ith length i-1th and i+1th value is the best case for being a triangle.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks. But I understood this one. I was asking for explanation to the solution using Fibonacci sequence.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        In Febo sequence 1, 1, 2, 3, 5.. observe all the consecutive elements just form degenerate triangle.

        So, if difference of smallest and largest value is smaller than F(n) (n is the size of array 'a') there exist 3 consecutive elements such that it form a triangle.

        F(45)=1134903170>(10^9) For n>=45 for any value dif(larg-sml)<F(45) so, triangle exist. For n<45 run a n^3 loop and check for all the triplet.

        → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I need help. I think this problem (Uva-10158 War) is very much similar to D. so I tried to do exactly what the author says to solve that problem.It matches all the i/o i found in the net.But still getting TLE. Don't understand why. this is my code: (code) thanks in advance :)

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    You haven't added any weight to the trees on Union. If you always add as first element as parent it would lead to linear time in parent_finding();

    Add a weight value to each node and take node with higher weight as parent. Weight would be the no. of element attached to it. Actually you have to take the element with larger height as parent but the weight would do as, for reaching 3-height atleast 5 nodes are required, and from there on the required nodes would double with each increment of height, for example 3-5, 4-10, 5-20, 6-40...

    Hopes that helps

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone please explain Div2 C? The solution is not clear to me.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Wrote DSU for D without reading the solution. My idea is exactly the same as others' but it won't pass test 10. No matter what I do, no matter how much I fix it this solution just won't pass test 10. Here is my cleanest and last version of the program. Still won't pass test 10. http://mirror.codeforces.com/contest/766/submission/24810631 What the hell is in test 10?

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can someone help for solving E using centroid decomposition?

→ Reply
»
15 months ago, # |
  Vote: I like it 0 Vote: I do not like it

CLEANNNN, tnx

→ Reply
»
5 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E can be solved by Centroid, its like dnc but on tree :D

→ Reply