Привет всем! Дальше я постараюсь объяснить решение задачи E Codeforces Round #132.
Давайте научимся решать немного другую задачу и будем искать число периодических чисел в полуинтервале (2k, x], где 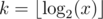 . Тогда видно, что x имеет длину len = k + 1.
. Тогда видно, что x имеет длину len = k + 1.
Теперь найдем блоки из единиц и двоек, которые, как раз, и являются общей частью периодического числа. У таких блоков, как следует из определения, длина является делителем длины всего числа len.
Теперь посчитаем число таких блоков g[i], которые имеют длину i, i делитель len. Возьмем старшие i бит числа x и назовем соответствующее число t = x >> (len - i), например если взять x = 100110002, а i = 4, то тогда t = 10012, а если i = 2, то t = 102. Первым делом, проверим подходит ли этот блок t, это можно сделать, например, посчитав p = ttttt..., где t повторяется 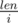 раз, p можно посчитать в цикле p = (p << i) + t. Понятно, что если p ≤ x, то посчитаем этот блок и сделаем g[i] = 1, иначе g[i] = 0. Все подходящие блоки должны быть меньше или равны t, и первая цифра у них обязательно 1, так как не может быть лидирующих нулей. Случай равенства мы уже учли, тогда осталось добавить к g[i] разницу между t и 2i - 1 = 10000...2, где i-1 нулей, g[i] = g[i] + t - (1 << (i - 1)). Может показаться, что все уже готово и можем сложить все g[i], где i делитель len, и не равно len, но нельзя. Покажем, что таким образом мы учли некоторые случаи по нескольку раз, например для x = 101011002, i = 4, g[4] = 1 + (10102 - 10002) = 3, мы посчитали блоки 1000, 1001, 1010, и если взять i = 2,g[2] = 1 + (102 - 102) = 1, мы учтем 10, но 1010 получается из 10 повторением два раза. Но эта проблема очень легко решается, для этого необходимо вычесть из g[i] все g[j], где j < i и j делитель i.
раз, p можно посчитать в цикле p = (p << i) + t. Понятно, что если p ≤ x, то посчитаем этот блок и сделаем g[i] = 1, иначе g[i] = 0. Все подходящие блоки должны быть меньше или равны t, и первая цифра у них обязательно 1, так как не может быть лидирующих нулей. Случай равенства мы уже учли, тогда осталось добавить к g[i] разницу между t и 2i - 1 = 10000...2, где i-1 нулей, g[i] = g[i] + t - (1 << (i - 1)). Может показаться, что все уже готово и можем сложить все g[i], где i делитель len, и не равно len, но нельзя. Покажем, что таким образом мы учли некоторые случаи по нескольку раз, например для x = 101011002, i = 4, g[4] = 1 + (10102 - 10002) = 3, мы посчитали блоки 1000, 1001, 1010, и если взять i = 2,g[2] = 1 + (102 - 102) = 1, мы учтем 10, но 1010 получается из 10 повторением два раза. Но эта проблема очень легко решается, для этого необходимо вычесть из g[i] все g[j], где j < i и j делитель i.
То есть мы считаем, своего рода, динамику.g[i] начиная с i = 1 до самого большого делителя len не равного len, и обновляем значения, вычитая соответствующие g[j].
Теперь мы научились считать количество таких чисел на полуинтервале (2k, x], перебирая все делители len и считая динамику g[i], и потом возвращаем сумму g[i], по всем делителям i < len . Заметим, что степень двойки не может быть периодическим числом. Теперь мы можем посчитать аналогичную величину для x = 2k - 1, дальше для 2k - 1 - 1 и так далее, пока не станет x = 1, теперь на этих непересекающихся полуинтервалах посчитаем сумму и вернем ответ. Это можно реализовать рекурсией. Вот мой код на C++, я дополнительно предпосчитал все делители для чисел до 60. Спасибо за внимание, надеюсь вам все понятно, а если не понятно задавайте вопросы)
UPD: Еще один код, который немного асимптотически быстрее.











А какова будет ассимптотика алгоритма?
По грубой оценке —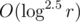 (на самом деле даже лучше).
(на самом деле даже лучше).Я плохо проанализировал, так что please ignore :).На самом деле здесь приведен не самый оптимальный алгоритм, т.к. например предпросчет делителей можно проделать за , во-вторых как не трудно заметить, если мы считаем ответ для степени двойки минус 1, то опять же ответ можно предпосчитать. Можно заметить что массив g[] будет одинаковым для всех чисел x вида 1111.., этот предпросчет осуществляется за
, во-вторых как не трудно заметить, если мы считаем ответ для степени двойки минус 1, то опять же ответ можно предпосчитать. Можно заметить что массив g[] будет одинаковым для всех чисел x вида 1111.., этот предпросчет осуществляется за 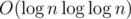 , так как известно что суммарно делителей у чисел от 1 до k всего
, так как известно что суммарно делителей у чисел от 1 до k всего  . пруфлинк. Ну а когда мы считаем для какого-то произвольного x, то оценка остается также
. пруфлинк. Ну а когда мы считаем для какого-то произвольного x, то оценка остается также 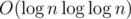 , так как на подсчет массива g[] нам требуется даже меньше операций, но если честно я не знаю можно ли сильно улучшить это оценку. То есть итог, все зависит от того, насколько быстро предпосчитать делители, но опять же я говорю про немного по-другому реализованный алгоритм, здесь я привел этот(с рекурсией) потому что он мне показался нагляднее, для тех кто считает иначе вот код
, так как на подсчет массива g[] нам требуется даже меньше операций, но если честно я не знаю можно ли сильно улучшить это оценку. То есть итог, все зависит от того, насколько быстро предпосчитать делители, но опять же я говорю про немного по-другому реализованный алгоритм, здесь я привел этот(с рекурсией) потому что он мне показался нагляднее, для тех кто считает иначе вот код
UPD: В коде была логическая ошибка, пофиксил.
мм обожаю это слово
Спасибо за минусы))) Никогда не понимал на КФ людей, которые минусуют, а причин не пишут. (это все потому что я зеленый да???) :-)
Возможно, потому что "аССимптотика" пишется с одной буквой с. Но если честно, я не знаю.
Хотя не, это потому что они боятся и им стыдно сказать это явно.
Евгений, спасибо за такое простое и понятное решение! У меня возник только один вопрос: как вы писали разбор не заакцептив свое решение на CF?
Почему же... на дорешке сдал я его. А на контесте придумал почти тоже самое, но не додебагал(
Я просто посмотрел ваши "попытки" из профиля и там не обнаружил сабмитов по этой задаче. Надо было заходить из архива в "Список решивших задачу".
Там, если я не ошибаюсь, а если ошибаюсь поправьте, отображаются "официальные" попытки, т.е. сделанные на контесте.
Предполагаю, так же, как я писал вот это, с той разницей, что я в своем разборе описал только идею.
UPD. Надо обновлять страницу перед отправкой комментария.