The competition at AtCoder has ended, I participated but couldn't solve F. The editorial link on the website is in Japanese, which I don't understand. Google translate doesn't give me a good translation or at least I cannot understand it. So can anyone share his/her solution to the problem or the solution from the editorial in english. Here is the problem for those that haven't seen it:
Suppose we have a line and N(N <= 10,000) pairs of points on it with coordinates (x_i, y_i). For each pair we can choose the first or the second point. We are to maximize the minimum distance between two consecutive points from the chosen(e.g when they are sorted on the line) which we can obtain by using different choices (whether to use x_i or y_i).











Shouldn't the problem be "maximizing the minimum distance between consecutive points" instead of "finding maximmum distance between consecutive points"
Thank you, I had it wrong. Now it's fixed.
Auto comment: topic has been updated by AnotherRound (previous revision, new revision, compare).
First of all you should notice that the answer is binary searchable. Now to check if the answer is possible we use 2-SAT. This can be done in a simple way in O(N2). But unfortunately if done like that the complexity will be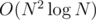 and also 2-SAT has a big constant. But you can notice that for each point you actually need just the previous points on at most middle distance from it. So if our current point we are looking at is xi then we need all points in the interval [xi - middle + 1;xi] and we need to add NAND closure between each of them and xi. This can be done with a segment tree or more like me will maintain some more nodes and we just need to add a closure between xi and the new nodes correspoinding to the segment tree nodes. This way we can check if some maximal distance is possible in
and also 2-SAT has a big constant. But you can notice that for each point you actually need just the previous points on at most middle distance from it. So if our current point we are looking at is xi then we need all points in the interval [xi - middle + 1;xi] and we need to add NAND closure between each of them and xi. This can be done with a segment tree or more like me will maintain some more nodes and we just need to add a closure between xi and the new nodes correspoinding to the segment tree nodes. This way we can check if some maximal distance is possible in 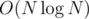 and so the overall complexity will be
and so the overall complexity will be 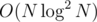 .
.
1) In which way is it binary searchable? If we can achieve distance d, we don't know whether we can do a smaller d or a larger d. (I just don't see why it is so, I don't claim what I said is true) 2) What exactly do we do with the segment tree? You mean that in 2-SAT instead of the points directly, we use the nodes of the segment tree? How do we manage it then if it's a graph(some point might be connected to children of some node, how do we handle this case), or what other implementation of 2-SAT should I use?
We can binary search on answer, as:
We actually binary search on D and check if the answer can be >= D. In the end we will be left with the optimal D. Think about it.
Now about the segment tree. We add edges from i to 2 * i + 1 and i to 2 * i + 2. Also for every point xi and yi look at interval [xi - middle + 1;xi + middle - 1] / {xi} and add edge from xi or yi to all nodes in the segment tree coressponding to the interval. Now you can notice that this is enouth to check if a distance is possible. Just run any SCC algorithm and check if for every i, comp[xi] ≠ comp[yi].
NOTE: When adding edges from xi or yi to the corresponding nodes we add the edge from the leaf of xi or yi. In such a way we guarantee that xi and all its neighbours will be in the same SCC.
I'm the writer of this contest. We found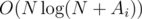 solution after contest (thanks sugim48).
solution after contest (thanks sugim48).
This solution was based on binary search and 2-SAT as well as intended solution. The difference is "we can get edge dynamically and we have to see only O(N) edges".
At first we double flags. After that we can describe this problem simple 2-SAT problem with 2N variable ("put i-th flag or not"). Second, sort all flags. Third, we manage flags by doubly-linked list.
In dfs part, we can get edge O(1) by checking adjacent flag in linked list. Of course we can remove edge O(1) by remove flag from linked list.
Thanks for preparing the contest.If possible, I hope next time you can translate the editorial for most difficult problems in the contest to English.