A. For solving this problem you might find some formula like
res = abc - (a - 1)(b - 1)(c - 1), res = ab + bc + ca - a - b - c + 1, or something else.
Also the problem can be solved in O(a + b + c) time — you can move from the top line to the bottom line of hexagon and sum number of tiles in every line.

Author is Ripatti .

B. You can build some graph where vertices are students and edges are enmities. You should drop some vertices and then paint them in two colors. Any edge should connect vertices of distinct colors and numbers of vertices of every color should be same.

You can see that graph consists chians, cycles and sepatated vertices. Every of that component can be painted in 2 colors except one case: cycles of odd length. So, you should drop one vertex from every odd cycle. After that you can get odd number of vertices. Then you should drop one more vertex (you can chose any of them). The obtained graph can be easily painted in 2 colors in the required manner.

Authors are Gerald , Ripatti .

С. The first solution: analysis of the cases
1. k = 1. For n ≤ m + 1 3 employees is enough (in most cases). For n > m + 1 answer is 2. Also, there are only one tricky corner case: for n = 2, m = 2, k = 1 answer is 4.
2. k > 1. If n = m, answer is 2k + 1, otherwise answer is 2k.
For any case it is easy to construct solution, and prove that this solution is optimal.

The second solution: greedy.
Let's create an array where we will store current number of employees for some number of the first days. Now you should iterate over all days from the first to the n + m-th and hire employees every time when it needed. You should hire workers if there are less than k people in the current day; also you should hire worker if there will be no people tomorrow (thet worker will bring the key to the workers that will work tomorrow).
This solution works in O((n + m)k).
This solution also works correctly for cases n < m, but then it has bigger complexity and requires more time.

Authors are Gerald , Ripatti .

D. For every sector you should sort bridges in order of increasing distance from the conter of the web. Now for every sector you should iterate over bridges of the current sector and two adjacent sectors using 3 pointers. During every pass you should carefully calculate number of bad cells. That is all solution.

Solition in 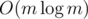, where m is total number of bridges.

Author is Ripatti .

E. Digital root of number is equal to that number modulo k - 1 for most cases. It is lie only for digital roots 0 and k - 1 — in that cases number modulo k - 1 will be 0. But you can get digital root 0 only for numbers like 00...00. Total number of numbers that type you can find using any other way. So, now you can find number of substrings that have some digital root, if you know number of substrings that equals some number modulo k - 1.

How to find number of substrings of some modulo? You should iterate over all digits of s from the left to the rigth and for every modulo store number of prefixes of that modulo in some array dp[] of size k. Let's current position is i. Then number of substrings modulo b that ends in position i equals to number of prefixes leftmost position i that have modulo (x - b)mod(k - 1), where x is modulo of s[1... i]. I.e. just dp[(x - b)mod(k - 1)].

To fit into memory limit, you should replace array dp[] by some associative array. For example, std::map from С++ or some hashtable.

So we have solution in O(nz), where z is complexety of access to dp[] ( for std::map and O(1) for hashtable).

Author is Ripatti.