This contest ended half an hour ago, let's discuss the problems.
How to solve problem K? We have found a thesis about it.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
This contest ended half an hour ago, let's discuss the problems.
How to solve problem K? We have found a thesis about it.
| Name |
|---|



How to solve F?
How to solve H (How to get yes/no answer for single strong connected component)?
H: You are to check whether all cycle lengths in SCC divisible by some p > 1. It can be done by dfs similar to bipartite graph checking (assign every node i value xi and solve system of equations: for every edge (a, b):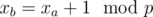 ). So if no such p exists the answer is YES.
). So if no such p exists the answer is YES.
P.S. You don't have to check all p, only the prime divisors of any cycle length.
There is simpler solution: https://en.wikipedia.org/wiki/Aperiodic_graph
I did a similar approach than explained on Wikipedia using BFS instead of DFS. But I don't understand why in the alorithm stated there, they compute the set of ke using the formula ke = j - i - 1. The set of ke for me represent the length of the cycles and I think they need to be computed like ke = j - i + 1.
it's j - (i + 1) because vertex on level j is also reachable in i + 1 steps
F: Let dp[L][R] be the answer for the subarray [L, R).
Which element can be the biggest in the subarray [L, R)? If the biggest element is the x-th one, x must satisfy x - r[x] ≥ L[x], x + 1 + r[x] ≤ R, and in at least one of the two inequalities, the equality must hold.
Thus,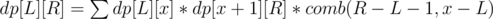 , where x moves over all possible xs. It turns out that there are O(N2) such triplets (L, R, x), so it works in O(N2).
, where x moves over all possible xs. It turns out that there are O(N2) such triplets (L, R, x), so it works in O(N2).
Can we just print "NO" if the result of dp is equal to 0? Or it is possible that the answer becomes multiple of mod and we need to check this case in some other way?
UPD: Yes, it is possible. Without handling this case you will get WA2. To handle it we also need to store in dp bool value "is there at least one appropriate permutation" and check it before printing the answer.
Yeah, gawry is kinda merciless.
I get this problem from Petr's blog. I misread problem as: radius as Min(smaller number on its left, smaller number on its right), not necessary continuous. Seems it's still solvable, due to there can be at most two possible position for Maximum element in a subarray. I implemented it fairly brutal and seems it can still calculate N = 1000 on randomly generated data. Do you guys think this "wrong" problem have polynomial solution? For clarification in "wrong" problem: radius for series [1, 4, 3, 2] is [0, 1, 1, 0], instead of [0, 1, 0, 0]. Truly appreciate.
F: let's find position of the maximum element. Its "circle" hits one of the borders and only leftmost position that hits right border with its circle and rightmost that hits left border could be the maximum. Maximum is not covered by any circle other thant its, so we reduce to two separate subproblems. How to implement: subsegment dp, for segment [l, r] you need to count number of correct ways to assign numbers from 1 to r - l + 1 modulo 109 + 7 and whether there is a correct way at all. After that iterate over two possible positions of maximum on segment. Iterate over two possible maximum positions (notice that they are chosen that way that reduction to two separate subproblems happens anyway), now you want to distribute r - l numbers to two groups of sizes k ≤ r - l and r - l - k and this is just product of two dp values of smaller segments and binomial coefficient.
It took me 2.5 hours to implement C. What's the simplest way to solve it?
I can't say for easiest, but this one did not require us 2,5 hours. Let's solve for connected components separately. If there is even number of edges in connected component, then we can match them all by dfs: for every vertex match its not yet unmatched son edges between themselves and possibly edge to parent, if this can't be done, edge to parent remains unmatched and we return it higher, to match it later This way all pairs are matched, because there can be only problem with root (root will have odd number of unmatched son edges), but this is not possible, because total amount of edges is even.
How approach hard case (component has odd number of edges)? We could delete edge with smallest weight but we can get two components with odd number of edges again after this operations (edge was a bridge). Now, it is never ok to delete ≥ 2 edges from the component, because all of them are bridges (otherwise we could delete only one of them and not ruin connectivity), this bridges separate our graph in some components after deletion (they are not necessarily biconnected, but there is still a structure of tree on them), so there is one of this component that is adjacent to ≥ 2 bridges, so we could instead create a perfect edge matching in this component (even number of edges) + this two bridges, so solution is not optimal.
Now we need to find such edge of minimum weight that it is not a bridge that separates our connected component into two components with odd number of edges and delete it (this completes reduction to easy case). It requires just finding bridges and sizes of subtrees in dfs that calculates bridges. precalculating bridges and
D: Let f(n) be the optimal sequence that achieves S(n).
Then it seems f(n) = f(n / 2) + "n" + f((n - 1) / 2) (here + means concatenation).
Why is this true?
Let's look: f(1)=1, f(2)=2+1, f(3)=3+1+1, f(4)=4+2+1+1, f(5)=5+f(2)+f(2)=5+2+2+1+1
But optimal sequence for n=5 is 5+2+1+1+1
All possible partitionings for n=5 is 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1
Sequence 5+2+1+1+1 is cover all of them and it's sum is less.
What is wrong?
You are not covering all sequences. Notice that the order matters, so sequence 2 + 3 is not covered.
For n = 5 one optimal sequence is 1 + 2 + 5 + 2 + 1.
It's clear
I miss the order of graffitti
P.S. I found http://oeis.org/A006218
Area covered by overlapped partitions of n, i.e., sum of maximum values of the k-th part of a partition of n into k parts.
Actually, the one you want is A001855
I searched it after generating it by hand during contest, but i have no idea why is it true.
To solve the problem you could just find a way to calculate the sum of f(i) for i in [1..n]. Using the fact that f(n) = n * ceiling(log2(n)) - 2ceiling(log2(n)) + 1
I did it like this (Warning: really ugly code)
I was wondering how you came up with this recurrence? Just observation from brute force code?
It took me some time, but I finally solved it: http://mirror.codeforces.com/blog/entry/50844.
Thank you, nice proof!
How to solve problem B?
Compute maxflow twice.
The answer is min(ans1, ans2). This can be achieved by water(e) = (f1(e) + f2(e)) / 2, oil(e) = (f1(e) - f2(e)) / 2.Why does it work?
I don't think the part about constructing water and oil flows is correct, it's quite easy to come up with counterexample(at least in general case, maybe it's correct under some assumptions).
The formula for the answer is still correct though.
Let ans = min(ans1, ans2).In the first graph, instead of finding the maxflow (ans1), find a flow that achieves ans. Call it f3(e). Similarly, define f4(e) for the second graph.Now, water(e) = (f3(e) + f4(e)) / 2, oil(e) = (f3(e) - f4(e)) / 2 should be correct.Edit: sorry, this proof is wrong.
http://imgur.com/a/yYO5x
How to solve J?
Denote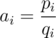 . Let's state our problem in such way: we have n linear functions
. Let's state our problem in such way: we have n linear functions 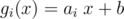 and want to find some subset of them and some ordering of that subset (i1, i2, ..., ik) that gik(gik - 1(... gi1(x)... ) is as big as possible. It is equivalent, because using fi from original problem is equivalent either to using gi or not using it and choosing best of this options. Now, we will just sort all linear functions by something and whether function actually does something or should be ignored won't bother us.
and want to find some subset of them and some ordering of that subset (i1, i2, ..., ik) that gik(gik - 1(... gi1(x)... ) is as big as possible. It is equivalent, because using fi from original problem is equivalent either to using gi or not using it and choosing best of this options. Now, we will just sort all linear functions by something and whether function actually does something or should be ignored won't bother us.
Now, let's look at optimal order of linear functions that we will actually use. It should satisfy such condition that we can't increase answer by swapping adjacent functions, so if the are two adjacent functions gi, gj (gi before gj), then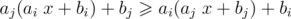 , so (aj - 1)bi ≥ (ai - 1)bj.
, so (aj - 1)bi ≥ (ai - 1)bj.
Now let's consider three cases: ai < 1, ai = 1, ai > 1. In first case our comparator is equivalent to , so it satisfies all qualities of good comparator (transitive and incomparablness is an equivalence relation), because it can be reduced to comparing fractions. In second case it is also ok, because it just checks whether 0 ≥ 0. Third case is similar to first one, only it is equivalent to
, so it satisfies all qualities of good comparator (transitive and incomparablness is an equivalence relation), because it can be reduced to comparing fractions. In second case it is also ok, because it just checks whether 0 ≥ 0. Third case is similar to first one, only it is equivalent to 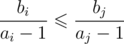 .
.
Now, let's think about order of functions of this three types (in each group we will just sort them by comparator). If we look at (ax + b) - x = (a - 1)x + b (our "profit" from applying the function) then we can see that for functions with a < 1 it decreases when x increases, for a = 1 it doesn't depend on x, and for a > 1 it increases when x increases. So, because x is non-decreasing in our process, we first should apply all functions with a < 1, then all functions with a = 1, then all with a > 1. To find order in each group we can use our comparator, which is completely ok, as long we are only comparing functions from one group.
Summary of solution: first use functions with ai < 1 in order of comparator, then with ai = 1, then with ai > 1 in order of comparator.
P.S. Better to use __int128 to compare fractions, but I believe that accurately written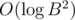 comparasion is also ok (where B = 109 — bound on numbers in input).
comparasion is also ok (where B = 109 — bound on numbers in input).
Comparison can be also made by firstly comparing in double (long double), if difference is "small" ( < 1018) — check difference sign computed in long long.
In problem K we thought about the EM-algorithm (alternate assigning bridges to stations and then calculating optimal positions of bridges for the assignment), but we sank in debugging and didn't have time for this. Have anyone tried this? If yes, was it successful? We don't know if it even should work
Optimal positions are known. Since loss function is linear on segment they are x and y projections of stations onto line. The problem is to choose optimal k of them.
Oops, I missed that the metric is manhattan, not euclidean
Retard
Respectful communication
It seems, you didn't hear Jinotega talks
Oh, so this is who they are.
https://twitter.com/Jinotega3000
K:
Let's parametrize our line by x-coordinate. Suppose a bridge is placed at point x. The distance from each police station to the bridge is a convex piecewice-linear function of x with 3 segments. Let's denote the x-coordinate of the minimum of this function as pi.
Now it's clear that: 1) We should always place bridges in one of 2*n junction points of those piecewise-linear functions. 2) If we have chosen all locations of bridges x1, x2, ..., xk, then each police station will go to one of the two bridges: the ones closest to pi on the left and on the right.
That allows to implement a O(k*n**2+n**3) DP. Our state is: how many bridges we have placed, and where was the last bridge. When we place the following bridge, for each police station with pi between them we determine to which one of the two it will go. Also, we need to take all pi's to the left of the first bridge and all pi's to the right of the last bridge into consideration.
Now we can speed it up to O(k*n*log(n)+n**2*log(n)). First, we speed up the construction of the "optimal placement between two given bridges" numbers. We can note that if we keep one of the bridges constant and move the other one away from it, then police stations will just flip at some point from the moving one to the constant one, and we can compute when they will flip and put those into a priority queue.
Then, we speed up the DP itself using the divide-and-conquer trick.
And finally, all this needs to be done in int64 (the only division is by a, so if we multiply all coordinates by max(1,abs(a)) all intermediate numbers will be integer), as double does not have enough precision.
Where can I see standings?
opencup.ru
Offtopic:
Whom should I contact to request an Opencup account for my university? As I see, it's an international contest so maybe it would be possible to get one.
E looks very similar to this problem http://acm.timus.ru/problem.aspx?space=1&num=2006
Can you please share your solution to the timus problem?
I got OK in upsolving using this paper.
How to solve G?
Greedy. First you go from left to right. If you get ( push the "removal cost" into a max-heap. If you get ), try to select an opening bracket from the heap. Which one? Of course the one with higher removal cost. What if there is no ( in the heap? Then this is extra ), so omit this ).
However, this is almost correct. It fails for: ()) with cost: 1 1 100. In this way you are selecting the last ) to omit, but it might be better to omit the middle one and keep the last one. But it works fine with (s.
How to fix it? Easy, keep another heap for )s. Whenever you match ) with some (, push the cost of ) into the heap. Now when you get ) but there is no ( remaining in ('s heap, that means this ) is extra. Now look at the )'s heap. You can replace any of the previous ) with current ). Which one should you replace? Of course the one with lowest removal cost. So check if the lowest removal cost of a ) in the heap is even lower than your current )? If so, pop out the previous ), and push the current ) with higher removal cost. So I guess you can understand that )'s heap will be a min heap. And you can easily compute the total cost while processing all these heaps.
How to solve B? K can be solved by divide&conquer optimization DP.
May be: http://www.cs.technion.ac.il/~itai/publications/Algorithms/2CF.pdf ?
Could you give me insights about some problems of XVII Grand Prix of Eurasia.