Choose for every given x minimal y among all points with this x. Since a > 0, b > 0 it`s reasonable to choose for bigger values of x smaller values of y. I mean the sequence of chosen y-values must be monotonically decreasing: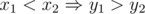 . Consider two functions: f(x) = ax and g(x) = by_x, where y_x denotes the y-value corresponding to the given x. One monotonically increasing while another monotonically decreasing. Seems like minimum of their sum may be found through ternary search by x.

Let v  <  u if v.x  <  u.x and v.y  <  u.y, consider the smallest points, red points in image, and apply a ternary search to minimize the function since necessarily with a, b  ≥  0 if u < v then A.u <= A.v (A = (a, b) and . is dot product), I hope you understand, I'm not good at explaining xD.