Errichto's blog

VK Cup 2017 Round 1 and CF Round 405 — Editorial
By Errichto, 8 years ago, In English
Tutorial is loading...

Code: 25627790

Tutorial is loading...

Code: 25627860

Tutorial is loading...

Code: 25627873.

Tutorial is loading...

Code: 25627885.

Tutorial is loading...

Code: 25627898.

Tutorial is loading...

Code: 25627911.

Tutorial is loading...

Code: 25627924.

Tutorial of VK Cup 2017 - Round 1
  • Vote: I like it
  • +51
  • Vote: I do not like it

Comments Comments (109)
| Write comment?
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by Errichto (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Can we use CenTroid Decompositions for problem D div 2 ??

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Yes. We got AC http://mirror.codeforces.com/contest/771/submission/25624241

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you explain how you did it?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it +4 Vote: I do not like it

        For example, the logic of the solution can be like this:

        In the centroid decomposition for each centroid we calculate the distances from all its vertices and store it in map. Now we use the theorem that on the path between two vertices there is one and only one centroid that contains these vertices. Then with the help of dfs we go around the centroid decomposition, in the centroid we calculate all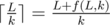 . All the vertices of the centroid are marked by those visited, climbing up the centroid tree to recalculate distances from the vertices that have not yet been visited.

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you :)

      → Reply
»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

And why my solution for F works? I tried to prove it for an hour and only after that decided to submit anything at the end. Why is it sufficient to suggest halfplanes between nearest points (sorted by angle) and the furthest from some till 180 degrees?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The editorial contains a proof but it will be refreshed only after the system testing, it's a technical "feature".

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can someone explain how to get the points "almost opposite p_1" for a point p_j?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Sort points by angle and use two pointers.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        But you have to sort points by angle with respect to p_i, not with respect to p_1. So naively, you have to sort the points one time for each point, which TLEs.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Everything should be done with respect to p1. So we sort points p2, p3, ..., pn with respect to p1.

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it +18 Vote: I do not like it

            Thank you for the response. It seems I didn't read the proof carefully enough. The question is beautiful :)

            → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

771C "Tutorial is not available"? edit: nvm

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Where is your code for problem C?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

All tutorials are already imported from Polygon. At the end of each tutorial you can find my code in C++.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +30 Vote: I do not like it

    When I click on submission link, it says that I am not allowed to view it.

    → Reply
»
8 years ago, # |
  Vote: I like it +7 Vote: I do not like it

in problem "Different Names"

"If the i-th given string is "YES", make names i and i + k - 1"

i think you meant if it is "NO"

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can "Different Names" be explained a little better?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Here's my approach.

    Iterate over given array s. If value is YES, make current sequence filled with unique names, otherwise repeat one value. To keep it simple, make first and last value of current sequence same. So, in next iteration, first k-1 names will be unique. You just need to decide whether to repeat first one or make it unique.

    Coding approach: First select k-1 unique names. Now, according to values of s[0] to s[n-k], if s[i] is YES, then generate new name and store it as answer of (i+k)th name. Otherwise, store answer of (i+k)th name as (i+1)th name.

    25618238

    → Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Not allowed to see the code

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can we solve problem B using BFS?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes you can

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes its your choice bfs or dfs. Although dfs seems easier.

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

For the Different Names editorial, it should be

First generate n different names. If the i-th given string is NO, make names i and i + k - 1 equal. Note that it doesn't affect other groups of k consecutive names.

→ Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I am not allowed to see the code !!!!

→ Reply
»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

My solution to the tree jump problem is O(nk). Precompute total path sums and count for each modulo for each subtree starting from bottom, then solve it again going down by subtracting your subtree from your parent node. Then sum up all the nodes, for runtime of 2nk+n

Code:25623074

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    mine too but due to smaller value of k our codes are slower than n*k*k due to recursion and extra constants maybe

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      My code is probably slower because I copy k length vectors around because I'm lazy, probably at least k times faster if I just use an array to store k values.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If not inconvenient to you, can you explain more detailed your solution? "total path sums" — to root? "count for each modulo for each subtree starting from bottom" — ?

    → Reply
»
8 years ago, # |
  Vote: I like it +10 Vote: I do not like it

There is something I don't understand about 771C - Bear and Tree Jumps solution.

what am I missing here? Isn't that the ceiling function? @.@

And, suppose k = 5 and a simple tree with edges 1 - 2 and 1 - 3. There are two paths with remainder 1, they have f(L, k) = 4 so I must add 2·4 to the answer?

Sorry if this is an extremely stupid question

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yeah, I'd like to understand that too...

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 5   Vote: I like it +6 Vote: I do not like it

      Pretty sure that its a typo. What he probably wants to say is that, if we find S and if we find , then 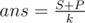. Here, countPaths(x, y) denotes number of paths of length x which give a remainder of y modulo k.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +6 Vote: I do not like it

        You are right. Should be fixed now.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          "We know the sum of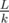 because its 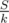in total"

          This seems wrong since we're dealing with Integer Division here, right? Don't we have to add S and P (see my definition above) before we divide?

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it +5 Vote: I do not like it

            Here we use normal division, not integer. We added f(L, k) to make normal division and integer division produce same result, and then we use only normal division.

            → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Thanks! The typo got me very confused haha

        → Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Can someone explain merging and how reminder is calculated in C, please?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain this solution of problem A(Bear and Big Brother)

submission link : 25610202

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    Apparently the desire number of years we are looking for is the solution for the following inequation: 3^i * a > 2^i * b, which is equivalent to i > (log(b) — log(a)) / (log(3) — log(2)). That's the O(1) solution for this problem.

    I did my solution like that at first, but the double precision caused a WA on some tests. Thus it is better to be careful working with floating number.

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

cheater caught anantheparty 25623078 jiangIy 25623055

just find some keywords in both codes like 0x3f enjoy the rating changes :D

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    Hey dude, you were out of competition in last contest......Why? and How?
    Did you cheated?

    → Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

It's a known problem to count the sum of distances for all pairs of vertices.

Is there some book that describes it?
Where does this problem come from?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +29 Vote: I do not like it

After I read tutorial for Div1-D (E in official round), I still don't get what exactly I have to do to improve the DP to O(n), especially how to calculate Ci. Can anyone elaborate that part more specifically? Thanks in advance.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Exactly :)

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Imagine the slower O(n2) solution that considers only particular O(n) states, including dp[i][i] (denoted as Ci). In my code in the editorial, the function go_from will be run only O(n) times.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why will it run only O(n) times?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 4   Vote: I like it 0 Vote: I do not like it

        Read the editorial just after "It turns out that the following values for each i are enough to solve the problem:". For each index i we will consider at most three states: dp[i][i], one dp[i][j], one dp[j][i]. Note that in two latter cases we have i < j.

        → Reply
»
8 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Can somebody explain this line of code in the given solution for the problem 771C Bear and Tree Jumps : int remainder = subtract(i + j, 2 * depth); why 2*depth?? Sorry if it's a silly doubt. Thanks in advance :)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    The formula to calculate the distance from u to v in a rooted tree is depth(u) + depth(v) — 2 * depth(LCA(u, v)).It is the similar.

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +12 Vote: I do not like it

Can anyone explain to me this part of code in problem C? I don't understand it even after reading the editorial and the comments.

for(int i = 0; i < k; ++i)
		for(int j = 0; j < k; ++j) {
			// compute distance modulo k
		        int remainder = subtract(i + j, 2 * depth);
			// compute x such that (distance + x) is divisible by k
			int needs = subtract(k, remainder);
			answer += (long long) needs * count_subtree[a][i] * count_subtree[b][j];
		}
→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 6   Vote: I like it +13 Vote: I do not like it

    Count_of_subtree[a][i] is no of nodes whose distance from root is i( where i=distfromroot%k ) and belongs to subtree of a including a.

    Now we want distance between each pair of nodes. This is calculated using normal, dist(u, v) = dist(u) + dist(v) — LCA(u, v), here all distances are from root.

    Thus we see all pairs, 0...K-1 to merge the two sub-trees. need is the f(L, K) that needs to be added( to allow total distance to be divisible by k ).

    Now how many times times f(L, K) would be added, it is no of pairs i, j such that need = K- ( dist(i, j) % K ), which is nothing but count_subtree[a][i]*count_subtree[b][j].

    In this way we recur up, and do it for all nodes. Here we use K(as MOD) to calculate distance between two nodes to avoid TLE by trying all nodes.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +6 Vote: I do not like it

      Thanks for your answer. But why do add total_subtree[a] += total_subtree[b] and count_subtree[a][i] += count_subtree[b][i] after we calculate answer?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        total_subtree[a] += total_subtree[b] because b is a child of a. To find out the total number of nodes in a's subtree, you recurse into every one of its children (here, b), compute their subtrees' total number of nodes, and then add it all up to a's subtree.

        count_subtree[a][i] += count_subtree[b][i] because count_subtree[u][j] means the number of paths starting at the root of the whole tree that end somewhere in the subtree rooted in u and have length j (mod k). Hence, if b is a child of a, then the paths described above which end in a's subtree include those that end in b's subtree (because a's subtree includes b's subtree, for all children b of a).

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      int remainder = subtract(i + j, 2 * depth); Can you explain this line to me? Why is the disance ((i + j) — 2 * depth) % k?

      → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Can someone please try to rephrase the explanation for Div2-D Bear and Tree Jumps? I followed both the text description and the author's code.

I could not understand the part with the two imbricated for loops over k inside the DFS. The author states he's "computting distance modulo k" then proceeds to subtract 2*depth from i + j, which are remainders as far as I can tell. What distance is this? What are we actually trying to achieve here?

Any visual explanation or suggestion for how to make sense of this?

LE: Alright, I think I got it, given two subtrees rooted in vertices u and v respectively, and given: number of paths Pu from the (global) root, having length i (mod k), that end in u's subtree, as well as number of paths Pv from the (global) root, having length j (mod k), that end in v's subtree, we're trying to compute the lengths of the paths between those vertices in u's subtree where paths Pu end and those vertices in v's subtree where paths Pv end, hence we employ the LCA-like formula...

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If problem div2 D. Bear and Tree Jumps asked to print the sum of the number of jumps from every node, could it still be done using one dfs? Or two dfs must be applied in that case?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I guess we would need centroids then.

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Yeah it could be done using two dfs. I used this exact approach to solve this problem. I calculated the number of jumps for each node to all other nodes, calculated their sum and print(sum/2) ! CODE Time complexity is O(n*k)

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain to me what's wrong with this submission please: http://mirror.codeforces.com/contest/791/submission/25671681

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve Bear and Tree Jumps? Can someone please explain in detail?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +4 Vote: I do not like it

    You can read: the editorial, comments under this blog, my code (provided in the editorial).

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In problem 771D, what is the intuition behind coming up with that particular state ? I could not come up with anything like it when I thought of it on my own. My ideas revolved around having states for a n length string and relating it with answer for (n-1) length string but I could not come up with anything that worked. Is this (the one in the editorial) a common way of choosing states for these type of problems ? If not, could you suggest how to learn to come up with them during contests ?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thinking about some particular moves and how the string looks like after a few moves turns out to be hard (I think you can't get a solution this way). Instead, sometimes it makes sense to think about the final string and this is a way to go in this problem. If you will try to create a dp state to know something about the final string, you should get the idea similar to the one described in the editorial.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I am confused with statement that is given in Bear and Tree jumps's editorial...

" We know the sum of L/k because it is S/k in total. "

it might be S/k ,,, and it might not be equal to S/k...

Even the first statement in the same paragraph says that answer is "AROUND" S/k, not exactly S/k... so am I understanding anything wrong there ???

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    S is defined as the sum of length (i.e. the sum of L), so S/k is equal to the sum of L/k.

    And yeah, the answer is something different than S/k, because the answer is equal to the sum of values L/k rounded up.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

It was a very interesting contest. It is sad that it is over

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Does anyone have a proof of correctness for the solution for 771B — Bear and Different Names?

I can't seem to understand why the other groups of k consecutive names are not affected if we place a duplicate at the start and end of each window of size k.

I can see that the the duplicate element at the start of each group will be shifted out at the next iteration. But why doesn't the duplicate element at the end affect the other groups?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Start by proving the following. We choose n different names and we make some two names i and i + k - 1 equal by replacing si + k - 1 = si. Do you agree that other groups of k consecutive names aren't affected?

    The second part is to notice that we can go from left to right and make that operation many times. The proof will still be correct. What matters is that last k considered names are different, not that all names are different.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      We choose n different names and we make some two names i and i + k - 1 equal by replacing si + k - 1 = si. Do you agree that other groups of k consecutive names aren't affected?

      Sorry. But I don't understand why the other groups of k consecutive names aren't affected.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        If group is affected it contains both this names (all other names are different), but it means that it contains all the elements in between too. So, it contains at least this k element, so no other elements(because it contains exactly k), but if it's this group, then it's not other group

        → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For 771C — Bear and the Tree Jumps, how did the author manage to derive that the solution for the sum of path length between all pairs of nodes is S/k?

Also, I do not understand why f(L,k) contributes to the answer. How does it help us to minimize path length between nodes?

Please advise.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The sum of path length is S — this is how I defined it. And note that we don't minimize anything. We use f(L, k) to get rid of the ceil symbol:

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Hi. Thank you for your quick reply. I understand your explanation but I do not understand why the answer is S/k. Also, if the solution does not minimize anything, why does it manage to compute minimum jumps between all pairs of vertices?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Also, if the solution does not minimize anything, why does it manage to compute minimum jumps between all pairs of vertices?
        There is only one path between any two vertices in a tree.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thanks! That clarifies half of my doubts. Do you know how the author got the expression S/k?

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Read my answer to papa-ka-para's comment (a few comments above).

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              I read the comment. Unfortunately, that was not the answer I was looking for. I am confused about how the expression S/k was derived in the first place?

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                S is defined in the editorial. I divided it by k to get the expression S / k. It you ask about something else, use some other words.

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  8 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  Sorry if I didn't make my question clear. Why do you divide S by k?

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  8 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  Because the statement says that we should find the sum of ⌈ L / k⌉, so computing the sum of L / k is a reasonable start.

                  → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why this code does not pass the tests?

27540821

The solution is based on KAN's code.

25627860

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 771C - Bear and Tree Jumps author states "For each subtree we compute the k values: for each remainder modulo k how many paths (starting from the root of this subtree) have this remainder." What does it mean that path starts in some vertex?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    "A path starts in vertex X" means "Vertex X is one of two ends of a path".

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem E(Rectangular strips), can anyone explain how to do the update operations in the dp and still manage to get overall complexity of O(n) ?? I am stuck on this part. Thanks!

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Hi KAN! In 771A's code 25627860, shouldn't the type of "cnt_edges" be "long long"?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I dont' know if this was a stupid question or not. Tutorial : "It's a clique if and only if edges = (vertices)*(vertices-1)/2" but in your solution you only check 'edges = (vertices)*(vertices-1)'. what's the difference ? And how could your solution work? Thank you very much!!

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I count every edge $$$(a, b)$$$ twice: once from vertex $$$a$$$ and once from $$$b$$$.

    → Reply
»
5 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it 
#include <iostream>
#include <vector>
using namespace std;
const int N = 150000;
int n, m, v_cnt, e_cnt;
vector<int> g[N];
bool used[N];

void dfs(int v)
{
    v_cnt++;
    used[v] = true;

    for (int next : g[v]) {
        e_cnt++;
        if (!used[next])
            dfs(next);
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;

        g[a - 1].push_back(b - 1);
        g[b - 1].push_back(a - 1);
    }

    int cnt = 0;
    for (int i = 0; i < n; i++)
        if (!used[i]) {
            v_cnt = 0, e_cnt = 0;
            dfs(i);
            if ((long long) v_cnt * (v_cnt - 1) != e_cnt) {
                cout << "NO" << endl;
                return 0;
            }
        }

    cout << "YES" << endl;

    return 0;
}

This code is for https://mirror.codeforces.com/contest/771/problem/A

I have taken this code of one of the user. Can anyone tell me why values of a and b are decremented by 1 before push_back operations?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It changes numbering from "1, 2, ..., N" to "0, 1, ..., N-1", which is better for programming because arrays are indexed from 0.

    → Reply
»
4 years ago, # |
  Vote: I like it +10 Vote: I do not like it

My Limak and Tree Jumping Problem is based on rerooting and has better complexity than the editorial: 92087472

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can we solve 771A — Bear and Friendship using dsu ? Someone please share solution using dsu if possible. Thanks

→ Reply
»
23 months ago, # |
  Vote: I like it 0 Vote: I do not like it

i solved problem C. Bear and Tree Jumps using REROOTED technique. i guess this approach is more easier to understandable than editorial solution.

→ Reply
»
6 months ago, # |
  Vote: I like it 0 Vote: I do not like it

sorry for necroposting.

for problem A, Bear and Big Brother, we want to find some year $$$k$$$ such that $$$a\cdot(3^k) > b\cdot(2^k)$$$

why it ends in some finite amount of operations? the editorial says we don't need more than $$$6$$$ operations

→ Reply