LoppA's blog

2-CNF Problem — Doubts
By LoppA, history, 8 years ago, In English

Hi I'm having trouble with the 2-CNF (Conjuctive Normal Form) problem, not just 2-SAT but the more general case of Conjuctive Normal Forms, ie: a => b (a implies b), c => ¬d (c implies not d). I've got some doubts, if you can help me with any of them it would help me a lot.

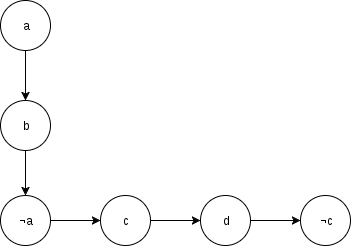
1 — What is the answer for the case (a => b) and (b => ¬a) and (¬a => c) and (c => d) and (d => ¬c)? I think its not satisfiable but if you solve like 2-SAT by just checking for all x if x and ¬x are in the same SCC then getting the variable with higher toposort between (x and ¬x) as the answer you may come to a diferrent result.

2 — There is an algorithm to find if some 2-CNF is solvable? And if its solvable how can we get some solution?

3 — If x or ¬x has not in edge nor out edge in the graph of implications, its correct to just set it as the answer? If you just get the toposort values like in 2-SAT algorithms, x or ¬x can be set as answer depending of how you do the toposort, but in some cases I think it doenst work.

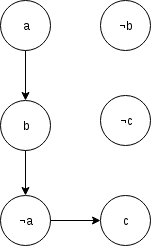
Ex: (a => b) and (b => ¬a) and (¬a => c). If we dont treat it the toposort of ¬c can be grater than toposort of c and ¬c may be setted as the answer, but it is mandatory that ¬a is in the answer so c is in the answer.

4 — There is a way to calculate the total number of ways of chose the values of variables to get a satisfiable solution?

  • Vote: I like it
  • +41
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by LoppA (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
← Rev. 4   Vote: I like it +18 Vote: I do not like it

What is the difference between 2-CNF and 2-SAT? As far as I know, 2-SAT is about satisfiability on CNF formulas where each clause has two literals (or at most two depending on the book, but these two versions are pretty equivalent).

Also, implications of the form can be easily written as a CNF clause as 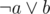. Note that if we go "backwards" from the disjunction 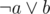we can get two implications: and (this second implication is sometimes called the contrarreciprocal). In fact, the inference graph of your first question is incomplete (and that's why you can't infer a contradiction) precisely for this reason: you did not add the contrarreciprocal of the stated implications. Let's list the complete list of edges:
(a => b) adds these two: (a -> b), (¬b -> ¬a)
(b => ¬a) adds these two: (b -> ¬a), (a -> ¬b)
(¬a => c) adds these two: (¬a -> c), (¬c -> a)
(c => d) adds these two: (c -> d), (¬d -> ¬c)
(d => ¬c) adds these two: (d -> ¬c), (c -> ¬d)

Note that there is a path from a to ¬a: a -> b -> ¬a
And a path from ¬a to a: ¬a -> c -> d -> ¬c -> a

Which forms the contradiction that makes this formula not satisfiable (so, you were right about the satisfiability of this formula).

I cannot answer your second question because I don't understand the difference between 2-CNF and 2-SAT.

About your third question: it can happen that x has no edges but ¬x has some. Imagine that x only appears at the clause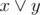 . Then, you will have two edges ¬x -> y and ¬y -> ¬x. However, I think that this is not sufficient to prevent x to take any value.

I like your fourth question. To be honest I have no idea on how to count fast the number of possible assignments.

→ Reply
»
8 years ago, # |
  Vote: I like it +11 Vote: I do not like it

I believe that questions 1 and 2 were already answered above.

Re. 3: yes, it's ok to do so, providing that you drew all necessary edges and you don't try to satisfy both x and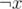 at the same time (e.g. if x has no constraints). Proof is simple: just make an arbitrary topological sort of vertexes and then move all isolated vertexes to end beginning/end of the order. You can do that because they are not restricted in any way.

Re. 4: see Wikipedia on that matter. No polynomial time solution was found so far, so I think your best bet is some kind of DP on subsets or a smart backtracking.

→ Reply