dj3500's blog

Helvetic Coding Contest 2017 online mirror
By dj3500, history, 8 years ago, In English

Hello CodeForces! This year again, I'd like to invite you to the online mirror of an open championship of Switzerland called the Helvetic Coding Contest. A mirror was also held last year — see here: Helvetic Coding Contest 2016 online mirror (teams, unrated)

The Helvetic Coding Contest is a yearly contest held at the EPFL in Lausanne by the PolyProg association. The contest itself took place on April the 1st, but the online mirror is scheduled on Sunday, 28th of May, 11:05 Moscow time. The duration is 4:30.

Rules:

  • you can participate in teams or individually (1-3 people),

  • standard ACM-ICPC rules (no hacking),

  • the contest is not rated,

  • if you have participated in the onsite contest, please do not participate in the mirror.

You will help us find the cow Heidi and participate in some April-Fools-Day confusion. The contest will feature 5 series of 3 related tasks with increasing difficulty (easy/medium/hard). Sometimes it may be the case that a solution for the hard version solves all of them, but usually not. We think that the problemset is diverse and interesting, and while the contest is ACM-style, you will find that some problems are not so standard. Most easy&medium problems are even solvable in Python, so you can also recommend this contest to your newbie friends :)

Acknowledgments: the problems were set by Christian Kauth, boba5551, meret, DamianS and myself. Thanks also go out to people who helped with the statements and testing: maksay, Michalina Pacholska (who also draws the cows), Benjamin Schubert, Aleksa Stanković, Ruofan Zhou; Tatiana_S for Russian translations and KAN for CodeForces coordination, as well as everyone involved in the actual onsite contest, who are too many to name here. We also thank the sponsors Open Systems and AdNovum. Lastly, thanks to MikeMirzayanov for CodeForces and Polygon (which was used to prepare the problems).

Finally, in a bit of autopromotion, note that you can use Hightail to automatically test your solutions :) Good luck!

After-contest UPDATE:

>>> Editorial <<<

Feel free to ask questions in this topic.

Thanks to everyone who participated! We hope you have enjoyed the problems. Congratulations to the winners:

  1. ★SweeT DiscoverY★: dotorya, zigui, molamola. (solved all problems!)

  2. japan-cookie: sigma425, sugim48, yosupo (solved all problems!)

  3. HSE Bluebell: Um_nik, Kronecker

  4. Veteran: I_love_Hoang_Yen, chemthan, ngfam_kongu

  5. m(_ _)m: tmt514, Shik, dreamoon_love_AA

  6. never red: xxTastyHypeBeast666xx, gongy, rnsiehemt

  7. rng_58

  8. (｀・ω・´): FizzyDavid, ohweonfire

The winners of the onsite contest (Petr Team) also solved all problems.

See you again next year!

Tags hc2
  • Vote: I like it
  • +105
  • Vote: I do not like it

Comments Comments (55)
| Write comment?
»
7 years ago, # |
  Vote: I like it +31 Vote: I do not like it

6 weeks ago xD

→ Reply
»
7 years ago, # |
  Vote: I like it +35 Vote: I do not like it

Why am I not able to register as a team?

→ Reply
»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

one computer per team?

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Why am I getting "Can't unregister. Possible reason: You made at least one action in the contest."

I want to be in a team with JustInCase and radoslav11 but it won't allow me to unregister :(

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    For what it's worth, I cannot see you on the registrants list either...

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve L?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I wonder for who didn't learn about Poisson distribution, is it possible to solve D without Google?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yeah, we just played a bit with some constants and it passed.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +44 Vote: I do not like it

    All information you need (i.e. the distribution function) was written in the statement.

    Try all 2000 distributions (2 types, 1 <= P <= 1000). For each distribution compute the probability that you get the given sequence. Find the distribution that gives the maximum probability.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      This sounds so obvious (and elegant!) that I wondered why I didn't think of this. Then I realized that I have no idea how to calculate the probability and even your code didn't help with that. After reading the editorial, I see that I had to know some formula.

      I don't think that someone who has to google Poisson distribution would know more advanced things about statistical analysis, like the formula you used.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +30 Vote: I do not like it

        Fix a distribution D, and let D(k) be the probability that this distribution gives k. Let a1, ..., a250 be the input.

        We want to compute the product D(a1) * ... * D(a250), but this is too small. I computed log(D(a1)) + ... + log(D(a250)) instead.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +15 Vote: I do not like it

          Thanks! That sounds both brilliant and dubious at the same time. I mean, if I came up with this by myself, I don't think I would convince myself that it's correct and there is no flaw.

          I don't know how to express my doubt, it just feels really weird to treat every input value separately. Of course I believe you and my math says it's correct but somehow my intuition still can't accept it.

          Is the G-Test described in the editorial equivalent to your measure? I always thought these tests were highly approximate and that there was no better way to test the statistics. Yet your way seems better and simpler. What am I missing?

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it +5 Vote: I do not like it

            Isn't this just maximum-likelihood estimation, essentially? Since the samples are drawn independently, the probability of the sample vector is the product of their individual probabilities. As rng_58 said, it is too small, so we take the logarithm. This is then called log-likelihood. Comes up all the time in statistics and in machine learning.

            This thing (MLE) gets even weirder when dealing with continuous distributions. There, the probability of having sampled any particular value (real number) is zero, but we take the probability density function at that value instead and it still somehow works... ;)

            → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

What is fast solution for B?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    My solution went like this: find the next position of every book for every element of the array (or inf if that's the last time you need it). For every book you buy put it in a priority queue and once you go over k books, remove the book at the head of the queue.

    I figured it'd be optimal to remove the book that was furthest away from my current position because it'd be more important for me to keep the books that are needed earlier so that I don't have to repurchase.

    Edit: ran in like 300 ms with Java.

    → Reply
»
7 years ago, # |
  Vote: I like it +20 Vote: I do not like it

For the last task, I assumed that the optimal solution for k + 1 is a superset of the optimal solution for k. Is this correct?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Yes (at least with 'an' optimal solution :) ).

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    You can model it as MCMF network (just for the sake of the proof, not actual implementation) and then this claim becomes obvious.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Yes, this is actually described in the editorial. Some people prefer to think of this as a min-weight bipartite matching instance (and the Hungarian algorithm also builds matched-vertex-wise increasing solutions).

      → Reply
»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

The editorial link has been added to the first post.

→ Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Auto comment: topic has been updated by dj3500 (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

How to solve last task with simple code? I implemented segtree with almost infinity integers...

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Great question! Maybe one of the two teams who have done so (never red 27411549, ★SweeT DiscoverY★ 27412140) could explain their solutions?

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Besides, congrats for squeezing this in the last minute :)

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 5   Vote: I like it +58 Vote: I do not like it

    There is a neat way to remove constraints about K.

    Let's think about this problem first: "Choosing a_i and b_js with same constraints with original problem and minimize sum of those values, but there are no constraints about how many pairs we can choose."

    Let's assume that we are solving problem above with new A and B arrays, which are defined as following: a'_i = a_i + t, b'_i = b_i + t, (t is some constant value, which can be negative number)

    If t = INF, the best way will definitely be choosing no pairs. If t = -INF, the best way will be choosing all the pairs, (a'1, b'1), (a'2, b'2)... Furthermore, as t increases, the # of pairs we have to choose will decrease. So, if we choose some "good" t for the problem (using parametric search with t), the best way for that problem will be choosing exactly K pairs. At that point, we can simply get the answer of original problem by subtracting 2*t*K from modified problem.

    If we don't have constraints about K, the problem becomes much easier! We still have to use similar idea with editorial, (I'm not sure about this point. It was not me completing this solution in our team.) but code becomes a lot easier to implement.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +30 Vote: I do not like it

      I used this trick for N, I binary search for t then use n^2 dp. Then I replaced it with a greedy algorithm to pass O. I don't know how to prove it though :(

      Basically, for each b, I either create a new matching with minimum a which is unmatched, or replace maximum b in an existing matching.

      Please let me know if anybody has a proof!

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 5   Vote: I like it +23 Vote: I do not like it

        You probably already got the proof, but leaving this here for future visitors.

        The way I see it, this is wqs binary search/IOI Aliens DP trick(at least for the DP). Intuitionally, we can see that the recurrence is concave, so we can use the trick here. Link

        Also, we don't need to add cost t to both A[i] and B[i]'s(as in dotorya's solution), just adding to A[i]'s and modifying DP to only take a B[i] after taking some A[j] (j < i) takes care of it, I think it is also easier to observe concavity in this DP(code: 27438988).

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +20 Vote: I do not like it

          Actually I was asking for a proof of my greedy algorithm, not the binary search.

          Your resources will be useful for others though, thank you :)

          → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

In problem C, how to find minimum-cost flow with flow value exactly k?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    You can make another sink T1 and an edge T -  > T1 with capacity k and cost 0.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    Or run your MCMF algorithm for k iterations.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

At the bottom of problem L it wrote

In her travels, Heidi has learned an intriguing fact about the structure of her social network. She tells you the following: The mysterious determinant that you might be wondering about is such that it does not cause strange errors in your reasonable solution... Did we mention that Heidi is a weird cow?

Hmm, I wonder how would the determinant of the system ever trouble with a participant while solving the system of linear equations. I didn't thought of including them in my consideration as they usally cost O(N^3) to compute, don't they?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

It looks like O(n^3) solution should get TL in N, but my 27410692 gets AC in 3.7s.

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +28 Vote: I do not like it

Sample input here http://mirror.codeforces.com/contest/802/problem/O looks weirdly similar to that one here http://main.edu.pl/pl/archive/pa/2013/rap :P. That's a great problem, so that's nice that more people got to experience solving it, but you got lucky no Polish guys who knew where this problem comes from participated because they would get AC in first 10 mins.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    That's a great problem, so that's nice that more people got to experience solving it

    Our thoughts exactly :)

    We estimated that not many such people would participate, and we were right (but also: one of the reasons this was unrated). On the other hand, some people seem to have had prewritten solutions to B (and some of them got RE due to too small arrays in their codes :P). We did anticipate that the problem would be known in theory, because it is a classical question, but didn't know that it was posed as a contest problem.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      For B, I remember at least that it was set at FARIO 2009 (a joint French-Australian contest) and the problem and solution was described in Last Supper from IOI 2012. I think it's one of the most standard problem that I haven't heard an official name for.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem N,I saw a few solutions using dp with binary search.Can someone please explain this approach.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I read the editorial and didn't understand the question H. Can anybody explain with an example?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    For k=1 we have s=a and p=a.

    Let's try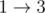 . We have p=a, u is empty and we arrive at p'=ab and s'=abbb.

    Now, let's try : p=ab, u=bb (because p+u=s), so p'=abc and s' = ab + c + bb + cc (I added + for clarity). You can check that indeed you can find "abc" in "abcbbcc" 7 times.

    One more example: . The only difference from previous one is construction of s'=ab+cc+bb+cc

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Thank you. There is something that i couldn't figure out. If I want to generate 6, what should I pick s and p for k=2?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        The simplest is s=aa and p=a but any pair such that p appears 2 times in s will be ok.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In K we had to find the subtree in which it would have possibly ended his journey for that in the editorial the approach is formulate another dp in which we store the maximum possible value if the journey ended in that subtree dp[node][true] but can't we just search for that unvisited segment that has a maximum value by keeping a global maximum variable and add that in our ans. Please explain why it is incorrect to do so? My Code 27472638

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    "can't we just search for that unvisited segment that has a maximum value by keeping a global maximum variable and add that in our ans "- NO this is not optimal

    5 2
0 1 100
0 2 2
2 3 5
2 4 3
a small test case .
    → Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The testcases for problem N/O are too weak.Some submissions can be hacked by

3 2
1 1 1
1 1 1

(The answer is obviously 4.)and/or

10 3
2 8 10 5 3 5 1 5 1 5 
7 2 3 10 4 7 7 3 9 6

(The answer is 15.)

→ Reply
»
16 months ago, # |
← Rev. 3   Vote: I like it +8 Vote: I do not like it

For 802O - April Fools' Problem (hard), here's a hint on the $$$13$$$ values likely referred to in the editorial:

Spoiler
→ Reply