Can someone help me in solving this question here.I had tried to solve it for hours but could not solve it.Later I watched the editorial but I am unable to get it.I understood the basic idea of role of bit being set 0 .But Still I am unable how this fact is incorporated in the solution . Can someone please help me with the problem ???? Thanks in advance and have a good day :)
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 21:30:06 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










I loved this problem. It was beautiful. I understood it in the following fashion:
Eg: Consider number 12 i.e (1100)2. Let at some stage dp[(1100)2] = 1101, then it means we are able to turn off the 3rd bit but 4th bit can't be set to 0 right now.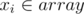 , and if still dp[12]! = 12, means 12 can't be formed.
, and if still dp[12]! = 12, means 12 can't be formed.
Read the following very carefully.
dp[(1100)2] = AND(xi), where xi is in array and contains 12 i.e xi&12 = (1100)2.
If we perform AND operation on all such
Then dp[y] &= dp[x], What does this do?
Clearly x contains y, and dp[x] tells us what bits we can turn off to reach as close to x. It's interesting to note that all those bits can also be turned off while trying to form y. So we perform dp[y] &=dp[x], and try to transfer all those 0 bits from dp[x] to dp[y]. Since x contains y, doing this operation will only help dp[y] to have 0s in appropriate bit positions and reach closer to y.
If you will look carefully, dp[x] is a number obtained by AND operation on all such numbers that contain x, and are present in array. Since x contains y, and we perform the AND operation, all those numbers are added to the AND collection of dp[y].
Now, just do the above DP operation, iterating from 106 to 1. At end, ans is number of x such that dp[x] = x Code
Got it .Thanks for reply .So basically we are trying to supply all possible zeroes that we have in a number x to all numbers y that can be formed from it through & operations .Thanks :)
I have another solution which is a bit different from the editorial's solution.
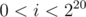 find the number of elements which are supersets of
find the number of elements which are supersets of  , lets call it
, lets call it 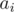 , then let
, then let 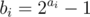 , on this do an inverse sum over subsets dp to find number of subsets with
, on this do an inverse sum over subsets dp to find number of subsets with 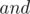 exactly equal to
exactly equal to  . This not only gives the values possible possible but also their count.
. This not only gives the values possible possible but also their count.
First using Sum over Subsets DP (Supersets in this case) , for each
Lastly this might overflow so use 2 modulos to hash it.
Code.
Also the last Div1 D is a bit similar (just change base 2 to base 10).
Thanks for the alternative approach but first I have to read SOS DP(I do not know that too :(
Your solution as well as the article you provided are very useful. I am the author of this problem and my initial solution was with a variation of FFT(Link). Thank you for sharing this approach with us. I did not know about SOS dp and now everything seems clearer. Your solution is also very ingenious.