Недавно был раунд, на котором многие участники ловили проблемы из-за отсутствия 80-битной вещественной арифметики в Java. Меня интересует вопрос (ведь исследования наверняка проводились), как же правильно складывать положительные вещественные числа?
Для желающих проникнуться темой я написал несколько реализаций сложения и проверил их на нескольких известных примерах. Реализации следующие: сложение в порядке возрастания, сложение в порядке убывания (всегда самое плохое :) ), сложение случайной перестановкой с последующей рекурсией через сумму левой и правой половины и сложение по принципу построения кода Хаффмана (последнее в действительности очень хорошо, но медленно).
http://ideone.com/OZIvET сложение в 32-битных числах для ряда 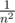
http://ideone.com/3SG8qm сложение в 64-битных числах для ряда 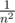
http://ideone.com/cWAvck сложение в 64-битных числах с разбросом 10
http://ideone.com/TB0loz сложение в 64-битных числах с разбросом 10000











Знаю, что есть такая штука. Насколько она полезна — не знаю. )
Работает, забавно. Оказывается, я упустил, что нужно просто провести вычисления с удвоенной разрядной сеткой.
А вообще я подумал еще немного, надо изучать вопрос. Википедия разбирает возможную оптимизацию по ассоциативности, которую, конечно, ни один адекватный компилятор проводить не должен. Но есть еще одна оптимизация — оптимизация неусечения регистра. Она заключается в том, что заявленное как 64-битное число загружается в 80-битный регистр и вычисления проводятся в 80-битном режиме, а результат приводится в 64-битный тип только при выгрузке из регистра в память. Такая оптимизация сломает весь алгоритм, если промежуточный t не будет переведен в 64-битный тип перед вычислением с.
Можно ссылку на задачу?
Обсуждалась следующая задача: сложить N вещественных чисел. Упоминалась в контексте задача 772A - Вечная Копилка