A. Маленькие числа
Для начала разложим числа a и b на простые.
Теперь заметим, что если какое-то простое число p входит в произведение ab в степени выше первой, то мы можем либо сразу поделить оба числа на число p, либо если же одно из чисел не делится на p, то перенесём в него множитель p из другого числа, после чего поделим на p.
Очевидно, что чётность вхождения простых чисел в произведение ab не меняется во всех операциях. Тогда давайте оставим все простые в первой степени. Остались числа p1, p2, ..., pn. Давайте назовём произведение всех этих простых чисел d, d ≤ ab. Утверждается, что этих простых не может быть больше 14. Если 1 ≤ a, b ≤ 109, то произведение ab ≤ 1018, а произведение первых 15 простых чисел превышает 1018) Теперь заметим, что конечный ответ — пара чисел (x, y) таких, что xy = d. Из этого следует, что второй элемент пары определяется однозначно по первому. Переберём всевозможные делители d за число x за O(2n), и выберем наилучшую пару.
B. Новая клавиатура
Используем для решения метод динамического программирования. Состояние — d[i][j][k], где i — флаг, обозначающий тип предыдущего действия (0, если это было переключение раскладки, и 1, если это был набор символа), j — номер текущей раскладки, и k — количество набранных символов. Значение — минимальное время, необходимое, чтобы достичь этого состояния.
Переберем k. Для фиксированного k переберем j от 1 до n два раза. Обновим d[0][j % n + 1][k] = min(d[0][j % n + 1][k], min(d[0][j][k] + b, d[1][j][k] + a)). Перебрать j от 1 до n два раза нужно потому, что после набора k-го символа может быть включена раскладка с номером большим, чем раскладка, в которой будет набран следующий символ, и будет необходимо произвести переключение раскладок по циклу до нужной. После этого переберем j еще раз и обновим значения для k + 1. Если в j-й раскладке есть k-й символ сообщения, d[1][j][k + 1] = min(d[0][j][k], d[1][j][k]) + c.
В конце ответ равняется min(d[1][j][m]), где m = length(s), по всем j от 1 до n.
C. Складывание фигуры
Заметим, что возможных линий сгиба ровно 4: две по горизонтали и две по вертикали, так как фигура должна полностью лежать с одной из сторон сгиба, а также касаться его.
Возьмем любую из клеток сложенной фигуры с минимальной координатой по оси OX — клетку (xi, yi). За линию сгиба возьмем вертикальную прямую x = xi, касающуюся этой клетки. Теперь слева нужно восстановить k - n клеток первоначальной фигуры, чтобы после складывания левой части вдоль линии сгиба на правую получилась данная во входных данных сложенная фигура. Так как k - n ≤ n (иначе после сгиба получилось бы больше n клеток), достаточно выделить из сложенной фигуры k - n клеток, образующих связную фигуру, содержащую клетку (xi, yi). Это можно сделать простым обходом в глубину.
D. Остроугольные треугольники
Для подсчета числа остроугольных треугольников достаточно из общего числа треугольников вычесть количество прямоугольных и тупоугольных треугольников. Будем считать три точки на одной прямой вырожденным тупоугольным треугольником.
Общее количество треугольников, которые можно построить с вершинами в заданных точках равно Cn3.
Заметим факт: количество прямоугольных и тупоугольных треугольников равно количеству прямых и тупых углов с вершинами в заданных точках.
Осталось посчитать количество углов не меньше 90 градусов с вершинами в заданных точках. Переберем угловую точку и отсортируем по углу относительно данной все остальные точки. Воспользуемся методом двух указателей. Переберем вторую точку, которая будет образовывать угол. Для подсчета количества подходящих третьих точек достаточно заметить, что все точки, которые образуют угол не меньше 90 с двумя другими точками, лежат на отрезке в отсортированном порядке и отрезок сдвигается только в сторону увеличения угла.
Время работы решения: O(n2log(n)).
E. Объединение массивов
Приведем два решения этой задачи — за O(k2·log(k)) и O(k2).
Решение за O(k2·log(k)):
Разобьем решение задачи на три пункта:
- 1) Для каждого массива X (A или B) и каждой длины 1 ≤ length ≤ |X| найдем minSubsequenceX[length] — лексикографически минимальную подпоследовательность X длины length;
- 2) Переберем длину подпоследовательности в первом массиве — 1 ≤ t ≤ min(k - 1, |A|). Если 1 ≤ k - t ≤ |B|, возьмем minSubsequenceA[t] и minSubsequenceB[k - t], их надо объединить;
- 3) Объединим две подпоследовательности в одну, получив тем самым лексикографически минимальную подпоследовательность длины k, обновим ответ.
1) Чтобы найти minSubsequenceX[length] для каждого length, выполним следующие пункты:
- Посчитаем next[i][c], в котором будет храниться следующее после i вхождение символа c в X;
- Посчитаем firstSymbol[length][i] — первый символ лексикографически минимальной подпоследовательности массива X[i..|X| - 1] длиной length. Для этого заметим следующее:
- Если j1 = next[i][1] существует, то firstSymbol[1][i], firstSymbol[2][i], ... firstSymbol[|X| - j1][i] начинаются с 1;
- Если j2 = next[i][2] существует, то firstSymbol[|X| - j1 + 1][i], ..., firstSymbol[|X| - j2][i] начинаются с 2;
- ...
- Если j|alphabet| = next[i][|alphabet| существует, то firstSymbol[max(|X| - j1, |X| - j2, ..., |X| - j|alphabet| - 1) + 1][i], ..., firstSymbol[|X| - j|alphabet|][i] начинаются с |alphabet|.
- Посчитав firstSymbol[length][i], можно восстановить лексикографически минимальную подпоследовательность X для каждой длины итеративно по одной букве.
Этот пункт работает за O(|X|2).
3) Найдя две лексикографически минимальные подпоследовательности SA и SB, их надо объединить в одну лексикографически минимальную длиной k. Будем двигаться по подпоследовательностям двумя указателями p1 и p2. Если SAp1 ≠ SBp2, то двигаем указатель, стоящий на меньшем числе. Если SAp1 = SBp2, двоичным поиском найдем наибольший общий префикс SA[p1..|SA|] и SB[p2..|SB|] и сравним следующие числа. Для сравнения подотрезков SA и SB можно использовать хеши.
Этот пункт работает за O((|SA| + |SB|)·log(max(|SA|, |SB|))) = O(k·log(k)).
Итого, суммируя все три пунта, получаем асимптотику O(|A|2 + |B|2 + k2·log(k)) = O(k2·log(k)).
Решение за O(k2):
Будем называть массив A нулевым, а массив B — первым. Будем строить ответ по одному элементу. Также будем поддерживать вспомогательное значение dp[i][j], где i — номер массива (0 или 1), а j — индекс в этом массиве. dp[i][j] равно минимальному индексу в массиве 1 - i, с которого можно продолжать строить ответ, если в массиве i мы остановимся на индексе j.
На t-й из k итераций построения ответа будем находить минимальный элемент, такой, что, добавив его в ответ, последовательность можно закончить, то есть что оставшихся элементов хотя бы k - t - 1. Также нужно учесть, что подпоследовательности обоих массивов, из которых строится ответ, должны быть обе непустые.
После добавления найденного элемента v в ответ, за O(|A| + |B|) обновим значения dp. Для обновления будем пользоваться посчитанным в предыдущем решении массивом next.
F. Два поддерева
По условию, в k-поддереве обязательно есть вершины на глубине k. Временно отменим это требование.
Рассмотрим все k-поддеревья для некоторого k. Их можно разбить на классы эквивалентности. Каждой вершине поставим в соответствие ck[v] — метку класса эквивалентности, которому принадлежит её k-поддерево.
При k = 0 все c0[v] равны, так как 0-поддерево любой вершины — это она сама.
При k = 1 c1[v] равно количеству детей вершины.
Научимся по массивам ck[v] и cm[v] строить массив ck + m[v]. Для начала, поставим в соответствие каждой вершине v массив arrk + m[v], который будет однозначно задавать класс эквивалентности её k + m-поддерева. Пусть u1, ..., us — потомки вершины v на расстоянии k в порядке обхода dfs. Тогда поставим в соответствие вершине v массив arrk + m[v] = ck[v], cm[u1], ..., cm[us]. То есть, k + m-поддерево вершины задаётся k-поддеревом вершины и m-поддеревьями нижней части k-поддерева. Ниже приведена иллюстрация для k = 3 и m = 1.
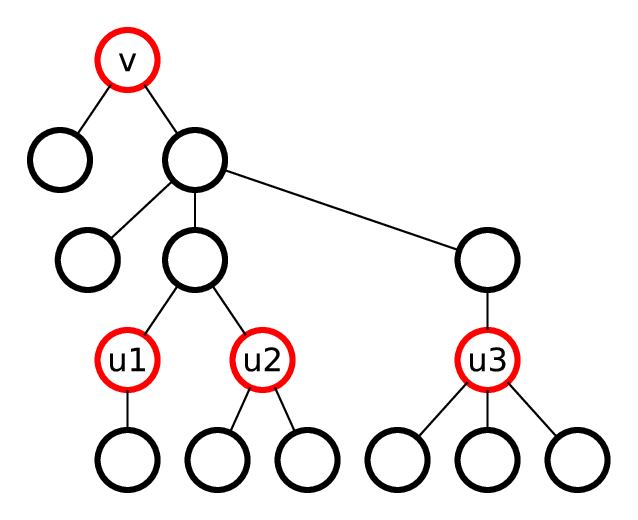
Чтобы получить для каждой вершины список её потомков на расстоянии k, запустим поиск в глубину от корня. Будем поддерживать в стеке путь до корня и каждую вершину класть в массив для её предка на расстоянии k.
Чтобы преобразовать массивы arrk + m[v] в числа ck + m[v], можно захешировать их, использовать бор или unordered_map из массива в номер. Время работы будет O(n), поскольку каждая веришна встречается в списках arr только один раз.
Имея массив ck[v], можно легко проверить, что существует два одинаковых k-поддерева. Для этого нужно найти две вершины с одинаковым ck, при этом нужно рассматривать только вершины, у которых есть потомки на расстоянии k от неё (это то требование, которое мы отменили в начале).
Чтобы найти максимальное k, посчитаем c1[v], c2[v], ..., c2t[v] (2t — максимальная степень двойки, не превосходящая n). После этого используем аналог двоичных подъемов по k: начнём с k = 0 и по очереди попытаемся прибавить к нему 2t, 2t - 1, ..., 20.
Время работы решения: O(nlog(n)).












How close can the answer in problem D (about triangles) be to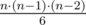 for a huge n?
for a huge n?
Tried to come up with several tests but answer turned out to be small all the time
If we take n vertices of regular n-gon then the answer will be about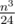 .
.
Could someone please paste their implementation of D (which they think is elegant)?
My solution (http://ideone.com/ahuhnB) is a little different from described here. For each point I generate a set of vectors from it. The number of right and obtuse triangles is equal to number of pairs of vectors with non-positive scalar product. To find it I rotate the vector and support the set of such vectors. Once it becomes co-directional with one vector I increase number of bad triangles by number in the set. Supporting it is quite simple since a vector enters this set from the moment it coincides with one of orthogonal vectors and leaves after it coincides with another. So I put into the set of events for each point 3 events: add point, query result, remove point. I start with vector slightly above vector (-1,0) and make a full circle counterclockwise.
In B, I think it will be
The answer is d[1][1][m] instead of .... The answer is min(d[1][j][m]), where m = length(s), for all j from 1 to n.