Hello CodeForces Community,
SnackDown 2017 Qualifiers has seen participation from over 21K teams across the globe. Of which 12859 teams have been advanced to Pre-Elimination Rounds. Complete list of the selected teams can be found here: https://www.codechef.com/rankings/SNCKQL17.
Problems of Pre-Elimination Round A are set by PraveenDhinwa (Praveen Dhinwa) and arjunarul (Arjun Arul) tested by kingofnumbers (Hasan Jaddouh). The rest of the panel members include:
- Russian Translator: CherryTree (Sergey Kulik)
- Mandarin Translator: huzecong (Hu Zecong)
- Vietnamese translators: VNOI team
Upon concerns raised by the community regarding the clash of timings between the May LunchTime and SnackDown Pre-Elimination Round A, the latter has been postponed by 2 hrs. The SnackDown Pre-Elimination Round A will now start at 27th May 11:00 PM IST (check your timezone here). We apologize for the inconvenience caused and wish you all the very best for both the contests!
We hope you will enjoy the problems and welcome your feedback in the comments below.
Start Time: Saturday, 27th May, 2017 at 23:00 HRS. (Indian Standard Time +5:30 GMT) Check your timezone here.
Duration:: 24 hrs
Contest link: https://www.codechef.com/SNCKPA17
Accepted Languages: https://www.codechef.com/wiki/list-compilers
Note: Teams in the top 1000 ranks move to the Elimination Round. Rest of the teams who could not advance to the Elimination Round through the Pre-Elimination Round A, get another opportunity to go to the Elimination round by taking part in the Pre-Elimination Round B.
Happy programming !!










How will rankings sorted? By count of solved problems or time also included here?
Sorry for bad english if struct of my question is not correct.
The ranklist will be score-based (ie ties will not be broken)
Gentle Reminder: Contest starts under a minute.
I keep getting error 405.
We are getting submission not possible, error 405! :(
There are soooooo many lags! I can get 405 after I press the submit button, after the following 10 F5's I obtain the same error, the next F5 leads to the proper page, after I submit my code I have 405, then 405, then 503 internal server error, then my code happens to be sent twice. Even if you just begin declining every code which is the same as the previous one, it'll be great
why? ties aren't broken.
Just in case if it matters. I feel a little uncomfortable anyway when I see that my code has been checked twice while it wasn't intended
Golovanov399 we regret the inconvenience caused. The error was there for a short duration and it was fixed. However, these things annoy while competing in a competition. We shall remain committed to ensuring such instances are not repeated. Once again we deeply regret for the inconvenience caused. Thanks for bearing with us.
Anti-venom please!
Somehow i made it this far. PraveenDhinwa I want to ask weather it's possible to add a member to my team now??
Any short approach for GAMEBALL? Also what is the minimum number of moves required to finish a game? Our solution never does more than 500 moves.
Can you describe your solution ?
Move the empty cell to top left corner. Now eliminate columns one at time taking care that there is always an empty cell available in the next column. For example you can do
3 1 1 1
1 1 2 1
1 2 1 1
1 1 3 1
Now eliminate the first column sparing one ball and repeat the process for column 2 and so on. The configuration after this step is complete easy to handle.
I did the exact same thing but got WA everytime. What were some corner cases you handled explicitly ?
for 1,1 and 2,2 the answer is -1
m = 2, n > 2 or n = 2, m > 2 can be corner case based on implementation. Also we got WA first time for not handling cases m = 1, n > 1 and n = 1, m > 1
5000 moves
Our solution does 328 moves in a 10x10 grid and the empty cell at bottom-right corner. Out solution also brings the empty cell at top-left corner first :)
If m >= 3, Then just keep repeating the same till the time there are more then 2 balls left. Move closest empty cell to (1, 1). And 2 other balls to (1, 2) and (1, 3). Then execute third query. Similar case for n >= 3.
This looks like 3*20*99 (> 5000) queries in worst case. However after first time, a third query is executed, an empty cell will always be in <= 2 distance to (1, 1). So that makes it around (2*20*99 + 2*100). In reality, the answer was always < 1200.
Enjoyable problem set! Although it should perhaps be called "SnakeDown" instead of "SnackDown", heh heh.
Can anyone explain the algorithm for "CONSESNK"?
In general, I'd like to know solutions to similar problems which I tried googling but couldn't find, like:
Is there a general name for this category of one-dimensional problems so I can search some archives or is it all just computational geometry?
You can apply ternary search on distance to be moved.
Code
Could someone explain the approach for 3rd problem 'A temple of Snakes'
What i did was to binary search on the possible start point in the [a,b] range. Let us consider I am at point x as starting point and now i will calculate the distance each snake will move starting from the snake (snake are sorted based on their starting position) and at this time i will also calculate how many snake lie left and right to the position where they have to placed according to point x. If left is greater then move left otherwise right.
I think you have explained the approach for 4th problem above. Could you explain for the 3rd one that is for 'A temple of Snakes' problem.
You want to maximize the height of the tower you build. If temple has height h, the cost is sum - h2. One solution is to precompute for each index the highest temple that can start at that index and the highest temple that can end at that index, and then binary search on h.
you can create two dp arrays one to right and the other to left , right[i] = min(right[i — 1] + 1 , arr[i]) , left[i] = min(left[i + 1 ] + 1 , arr[i] ) then at any position you can know what is the maximum hight for the temple and calculate the number of moves needed then minimize.
sorry for bad english
How did people use ternary search for Problem D (Consecutive Snakes)? Doesn't the function have plateaus i.e. f(x) = f(x + 1)?
You are right. I ternary searched with interval divided in 3 parts, and it should've passed. I was very confused that it didn't. Now I see why. The model solution was based on interval divided in 2 parts, and that is wrong.
So this problem should be either taken off the contest, or solutions should be rejudged.
Um, how? If f(l) = f(r) how do you know which part to cut off? Here, l and r denote the 2 points you check.
As long as there is only one extrema, it's easy, no matter where the plateau is.
eg:
Consider plateau coinciding with the extrema. This case is trivial.
Now consider the plateau is either on left or right. As ternary search for minima will try to cut off the larger branch, ie: if f(left) > f(right) : LEFT = left, this ensures that plateaus don't affect the search. Notice that in ternary search(with interval divided in 3 parts), left and right branches never overshoot the extrema. This is important, and is the reason why TS(with interval divided in 3 parts) works on any unimodal function.
in this problem, if f(l) == f(r) you are already on the top (both l and r are optimal)
UPD: sorry if f(l) == f(r) then l and r are not necessary optimal but if they are not optimal then you are sure that the optimal point is between them so ternary search is still applicable here.
Wait so you're saying the plateaus can only happen at the minima? Why is this true?
This assumption is wrong. Your logic about dividing the interval in 2 parts and checking mid, mid+1 not working for TS is right.
Yes in this particular problem. but in general you should check that plateaus will not happen other than on the top in order to apply ternary search.
Only if there is exactly one plateau at the bottom, but there can be more than one plateau on the sides as well.
Uh, optimal point can also be before l or after r if there are plateaus... What am I missing?
The only possible plateaus in this problem is in the top (by top I mean the most optimal points)
Can you give counter-example if you think I'm mistaken?
Cool, just wanted to confirm this. Idk how to prove it though
Can you show how it's only possible to have at most one plateau at extrema ? My TS with
doubleinstead ofintfailed, so I'm very curious what's actually the matter with this question.Heyy I_love_Captain_America can u plz define TS? Its used everywhere but I can't figure out its full form.
Plus I also used ternary search with 3 segments and it gave WA? So was my logic incorrect or test cases were incorrect?
Gee, I guess what TS could mean?
Heyy animeshf
TS: Ternary Search
How dumb I could be? :)
Can u plz clear why ternary search with 3 segments gave WA?
See this : http://mirror.codeforces.com/blog/entry/43440
So, in general, ternary search on integers don't work with interval divided in 3 segments. So, during contest, I changed everything to double, and finally took
min( f( (int)a ),f( (int)(a+1) ) )I can't believe even with double TS can fail.
There's an assumption here with TS o integers technique, that there can be only 1 plateau at the bottom, and I can neither prove nor disprove it in the case of the given problem.
So, just confirming:
Plz confirm this.
Ternary search with integers: Use 2 segments only when there's at most 1 plateau coinciding with extrema. If there can be many plateaus then no. In that case, change int to double. However this exact same technique failed for me, and I'm trying to find some answers too.
f(x) will be first be non-increasing and then only non-decreasing. So, if f(mid) = f(mid + 1), we know that for all points x less than mid, f(x) will be ≥ f(mid). So, we can safely shift to the right in this case.
Note that the non-increasing/non-decreasing part can also hold for 0 points in some cases.
When f(mid) = f(mid + 1), how do you know if you're in the part which is increasing or which is decreasing? For example,
No you're not. You're here as well as there at the same time, at all times. I mean you are on both sides of minima at any given time, unless both these point coincide(at minima). TS(by dividing interval in 3 parts) never overshoots.
What are you saying? mid can be on either side, so when f(mid) = f(mid + 1) where do you go? Do you do r = mid - 1 or l = mid + 1? Choosing which one requires knowledge of whether you're in the increasing portion or decreasing portion, right?
I used some other definition, first of all.
Maybe that's what I'm doing wrong, although I read it once in wikipedia. [I seriously think my approach should've worked]
And with your approach, even I am unconvinced how TS works. [maybe they should check their test cases again!!]
It is not wrong. There's at most 1 contiguous interval [l, r] where f(i) = f(i + 1). Think of the answer as you shift to the right, there are spots where you'll increase the answer if you shift to the right and the other spots you'll decrease (increase means the snake is to the left or same spot and decrease it's to the right), f(i + 1) = f(i) + increase — decrease. One spot starts out as decreasing (on -infinity) and can only go to increasing once, from increasing it can't go to decreasing. This means that this function (the difference) is (not strictly) increasing. Now, there can't be 2 intervals that have difference 0 since the (difference) function is increasing. It is actually a binary search on the derivative, not a ternary search.
Edit: Can someone confirm the O(n) solution, given that the snakes are given in order subtracing i * Length and finding the median?
I figured something too. The plateau corresponds to the region where cost of : moving x snakes from left to right + moving y snakes from right to left is constant. Also, x == y on plateau of length > 1. However, on the immediate next point on right side of plateau,
x -> x+1
y -> y-1
Therefore, cost of moving all snakes to further right increases with increasing x, as cost_to_move_right( new_x ) > cost_to_move_right( new_y ),
and the total cost = cost_to_move_right( new_x ) + ( -( cost_to_move_right( new_y ) ) ), which keeps increasing. This is because newx can only be greater than newy on right, so every shift to right increases contribution from newx that can't be compensated by newy's shift to the right. So, in each shift to right, we add newx-newy to the cost.
Here, newx == number of snakes, that always move right from their initial given position considering a particular starting point to form the queue,
and newy == number of snakes that move left with respect to the starting point to form the queue, and on each shift of the starting point to right, they move closer to their original given position.
Ignore.
And my approach should!!! Looks like their model solution itself is wrong. PraveenDhinwa please look into this.
Can you share your username on codechef or the solution of D problem which you submitted?
Dude even we had the same doubt . Maybe using the formula for could help
could help
if f(X) = f(X + 1) then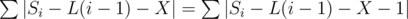 .
.
In LHS if there are p positive summands .
Then RHS = LHS - p + N - p = > RHS = LHS + N - 2p if LHS = RHS then we get p = N / 2.
Which means that if we have N / 2 positive summands then f(X) = f(X + 1) . But I couldn't show that this can happen only at the minima
Can someone tell me why my solution fails?
I tried on test cases which I could generate, it gave me correct answer but I get WA on codechef. So, can someone help.
While solving the problem I used a stress-tester . You can find the instructions to run the tester in the comments.
I found that we can begin the consecutive snakes from A to B — N * L and the optimal solution my be between them if you sorted the beginning of every snake and let the optimal solution at X then the result of X + 1 is greater than the result of X and X — 1 too so i used ternary search and got correct answer
The function can be transform into the form:
|x - a1| + |x - a2| + ... + |x - an|
Each |x - ai| is a convex function, so sum of them will also be convex.
So f(x) = f(x + 1) will only happen when you are at the optimal point.
Can someone explain their approach for the problem Protecting the poison. Also when the upsolving will be enabled.
I created 2 segment trees for vertical and horizotal, then coordinate compression. Notice that the same snake cannot protect both horizontally and vertically, as no snakes are allowed inside poison room. Therefore, we can separately solve horizontal and vertical.
I did a type of DP on segment trees. After separating the snakes horizontally and vertically, we can apply the solution on both set of snakes separately.
dp[ 1 + far_right[snake.l-1][snake.r] ][snake.r] = min ( dp[snake.l-1][snake.r] ) + 1
where far_right[a][b] is the rightmost position that has the value min ( dp[snake.l-1][snake.r] ).
The complexity can be brought down by maintaining segment tree to do dp.
Greedy solution can be proved too.
You are given some intervals [li, ri], you need to cover another interval [s, e] with minimum number of intervals!
First sort the interval based on l, break tie with increasing r.
Now start with point s, to pick next interval you need to find an interval such that li ≤ s and ri is maximum, then advance to that ri. This always leads to optimal solution.
Finding such interval with ri maximum can be done with two pointer. Alternatively we can also Binary Search to find the last index where li ≤ p and use segment tree to find the maximum r in that range.
Yeah, I knew some greedy solutions were there, but I had already thought of dp, so I coded it.
I_love_Captain_America Can you please explain your dp solution in more detail? Thanks.
snakes : [2,10] [4,8] [6,12]
dp[ 1 + far_right[snake.l-1][snake.r] ][snake.r] = min ( dp[snake.l-1][snake.r] ) + 1
dp :
0) [0] inf inf inf inf inf inf inf inf inf inf inf initialization
1) 0 [1 1 1 1 1 1 1 1 1] inf inf dp[ 1 + 1 ] to dp[10] = dp[2-1] + 1
2) 0 1 1 [1 1 1 1 1] 1 1 inf inf far_right == 8, so we can skip this step, as idx[8] already is minimum
3) 0 1 1 1 1 [1 1 1 1 1 2 2] dp[1+10] to dp[12] = dp[10] + 1
Well, the problem is reduced to finding minimum number of intervals that can cover our range from (N — K)/2 + 1 to (N + K/ 2). So, just sort all the range according to their starting points and then keep on going for every range with starting point <= (N — K)/2 + 1, find the largest ending point. After that keep repeating the same.
I solved it with greedy approach .It's easy to see that snake can defend poison vertically or horizontally,so we will solve them seperatly.Problem is equivalent to pick the least number of intervals (snakes) such that their union is interval [(n-k)/2+1,(n+k)/2].So sort snake wrt to their left bounds of intervals,and set variable x=(n-k)/2+1,so in the interval of snakes such that l ≤ x we will pick one with largest r (right bound of interval),and update x = x + r,if we can't find snake such that l ≤ x return -1 else continue with algorithm untill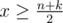 .
.
I hope elimination round problems won't bee about snakes,it's becoming boring :(
PraveenDhinwa
Can u plz share add the problems to practice and share the link over here?
All the problems are already available in practice section. For accessing them directly, you can remove "SNCKPA17" from URL, and go to practice page directly.
Example:
Contest problem: https://www.codechef.com/SNCKPA17/problems/TEAMFORM
Practice problem: https://www.codechef.com/problems/TEAMFORM
How to solve SNTEMPLE (A temple of snakes) if it's allowed to increase height as well ?
Sorry I misread your comment
I'd try something like this:
Fix the middle, notice that if you calculate f(x) (going x to each side), it will be a sum of
a[i] if x < |i — mid| and |a[i] — |x + 1 — |i — mid||| = |a[i] — (x + 1 — |i — mid|)| otherwise.
This means that it will be constant for some time and then it will be something that goes down and then it goes up (each part of the sum that is). This also means that the minimum will be on either the extremes of the possible interval or in the transition point from the downwards slope to the upwards slope of some part of the summation. This means that you solve only decreasing the same way you would normally and then for each i, guess that a[i] will be on some side or on the middle of the temple or the sides go until they can't grow (fixing a[i] in the middle) and you'll find the best answer.
To find the answers outside the normal part, use a trick like this: have 2 arrays where l[i] = a[i] — i and r[i] = a[i] + i. Use a merge sort tree to answer queries of the type: sum of elements in a range of an array where arr[L <= i <= R] <= k and you'll find each answer quickly. For example:
a = 1 2 3 2 1, l = 0 0 0 -2 -4, r = 2 4 6 6 6. You should use l to get the cost for the left part and r for the right part (don't forget to sum the parts where it should be 0). The cost of each side will be something like:
((number of elements <= constant) * constant — sum of elements <= constant) + (sum of elements > constant — (number of elements > constant) * constant)
If you put a sequence of a temple in l, the left side should have the same numbers and in r the right side should have the same numbers. The constant is the value of l[i] and r[i]. This same trick can be used to transform some strictly increasing problems to not strictly increasing (for example http://mirror.codeforces.com/problemset/problem/713/C). Given that this solution works, it has a complexity of O(nlog^2n) or O(nlogn) if using fractional cascading.
I'm not sure if this problem is even solvable, this is just a idea :P, it seems I overlooked some important things
For double ternary search, there can be more than 1 plateau( f(i)==f(i+1) ) still it finds the extrema, however function should be unimodal( increasing( could have f(i)=f(i+1) ), later finds the extrema, and then minimum( could have f(i)=f(i+1) ) ).
Please clear this out.