Hello!
This very hard DP problem from NWERC — regionals 2008 has the following editorial:

the editorial's code is also here.
I do not know if the editorial and the code share the same ideia, but i believe they are at least very similar.
Regarding my doubt, I do not understand why only the heights of the form hi + x*d are relevant (x from [-N+1, N-1]). (I undestood that the vector posh has all the possible different relevant heights in order, but I did not understand why to use that). I also did not understand the dp part using the vectors next and best in the code.
Can someone please help me?
Thanks a lot in advance!











Let's do straightforward dpi, j — minimal number of changes to make everything good on prefix of length i such way that last stack has j stones.
For fixed i, dpi, j is a piecewise linear function, in which segments' endpoints has form of ax + n·d. Let's imagine dpi, j has segments' endpoints с1, c2, ... cn. The function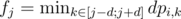 can have endpoints c1, c1 ± d, c2, c2 ± d, ... , cn, cn ± d. (Just imagine a window of size d, going through function dp_{i, j}. Something changes only in points of form ci, ci ± d). And
can have endpoints c1, c1 ± d, c2, c2 ± d, ... , cn, cn ± d. (Just imagine a window of size d, going through function dp_{i, j}. Something changes only in points of form ci, ci ± d). And 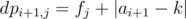 , so endpoint ai + 1 adds.
, so endpoint ai + 1 adds.
Linear function takes it's minimal and maximal values in endpoints, so we can calculate dp only for points of form ax + i·d. Now we have O(n3) states and calc every state in O(n2) time, having O(n5) total complexity. To make it work faster we need to do RMQ on previous layer. For example you can do it with monotonic queue, because it's minimum in window.