Hi, in this problem from HackerRank we abstract the problem to a directed graph with capacity and cost on the edges, source and sink and we need to get the minimum cost despite the flow (as long as we don't exceed the capacities).
To achieve that, we just need to change the Max Flow Min Cost algorithm breaking it when the best augmenting path we found has total cost greater than zero. Link to editorial: here (he changed the problem to Maximum Cost so he breaks it when the best augmenting path has cost smaller than zero).
My doubt is: Does this algorithm to get Minimum Cost with "Any Flow" work specifically for this problem's class of graph or does it work for every other cost-flow graph?
I belive you can do it anywhere since there is a way to keep the same old algorithm and modify the flow network in such a way that we get the minimum cost despite the flow.
What do you mean by modifying the flow network?
Here is an idea, if you have edges linked to the super-source of type (capacityi, costi), create a new node which will be the actual source and link it with the former source with an edge of type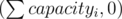
and also link this former source with the sink with the same type of edge. This way, a flow unity will never travel on a path of negative cost because it can take the source -> former source -> sink path of cost 0.
Yes, now its clear for me that it works. I changed my code too and passed with this idea, its easier too see the correctness of the approach thinking this way.
Thanks bciobanu!