Greetings!
Codeforces Round 418 (Div. 2) has just come to an end. This is my first round here, and hope you all enjoyed the contest! > <
Seems the statements still created a few issues :( Anyway hope you liked it, and the characters feature the Monogatari anime series. Let me state again that the statements has little to do with the actual plot — they're inspired by five theme songs actually — and I'm not spoiling anyone of the series! ^ ^
Sympathy for those failing system tests on B... This problem was intended to experience a lot of hacks but somehow there are not so many.
Here are the detailed solutions to the problems. Feel free to write in the comments if there's anything incorrect or unclear.
#include <cstdio>
static const int MAXN = 102;
int n, k;
int a[MAXN], b[MAXN];
int main()
{
scanf("%d%d", &n, &k);
int last_zero = -1;
for (int i = 0; i < n; ++i) {
scanf("%d", &a[i]);
if (a[i] == 0) last_zero = i;
}
for (int i = 0; i < k; ++i) scanf("%d", &b[i]);
if (k > 1) {
puts("Yes");
} else {
a[last_zero] = b[0];
bool valid = false;
for (int i = 1; i < n; ++i)
if (a[i] <= a[i - 1]) { valid = true; break; }
puts(valid ? "Yes" : "No");
}
return 0;
}
#include <cstdio>
#include <algorithm>
static const int MAXN = 102;
int n, k;
int a[MAXN], b[MAXN];
int p[MAXN], r[MAXN];
inline bool check()
{
for (int i = 1; i < n; ++i) if (r[i] <= r[i - 1]) return true;
return false;
}
int main()
{
scanf("%d%d", &n, &k);
int last_zero = -1;
for (int i = 0; i < n; ++i) {
scanf("%d", &a[i]);
if (a[i] == 0) last_zero = i;
}
for (int i = 0; i < k; ++i) scanf("%d", &b[i]);
bool valid = false;
for (int i = 0; i < k; ++i) p[i] = i;
do {
for (int i = 0, ptr = 0; i < n; ++i) {
r[i] = (a[i] == 0) ? b[p[ptr++]] : a[i];
}
if (check()) { valid = true; break; }
} while (std::next_permutation(p, p + k));
puts(valid ? "Yes" : "No");
return 0;
}
#include <cstdio>
#include <cstring>
static const int MAXN = 1e3 + 4;
int n;
int a[MAXN], b[MAXN];
int pa[2][MAXN], pb[2][MAXN];
inline void try_recover(int *a, int *p1, int *p2)
{
int dup_ct = 0;
int dup1 = -1, dup2 = -1, absent = -1;
for (int i = 0; i < n; ++i)
for (int j = i + 1; j < n; ++j)
if (a[i] == a[j]) dup1 = i, dup2 = j;
for (absent = 1; absent <= n; ++absent) {
bool occurred = false;
for (int i = 0; i < n; ++i) if (a[i] == absent) { occurred = true; break; }
if (!occurred) break;
}
memcpy(p1, a, n * sizeof(int));
memcpy(p2, a, n * sizeof(int));
p1[dup1] = absent;
p2[dup2] = absent;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
for (int i = 0; i < n; ++i) scanf("%d", &b[i]);
try_recover(a, pa[0], pa[1]);
try_recover(b, pb[0], pb[1]);
int *ans = NULL;
if (memcmp(pa[0], pb[0], n * sizeof(int)) == 0 || memcmp(pa[0], pb[1], n * sizeof(int)) == 0)
ans = pa[0];
else ans = pa[1];
for (int i = 0; i < n; ++i) printf("%d%c", ans[i], i == n - 1 ? '\n' : ' ');
return 0;
}
#include <cstdio>
#include <utility>
static const int MAXN = 1e3 + 4;
int n;
int a[MAXN], b[MAXN];
std::pair<int, int> get_duplication(int *a)
{
static int occ[MAXN];
for (int i = 1; i <= n; ++i) occ[i] = -1;
for (int i = 0; i < n; ++i) {
if (occ[a[i]] != -1) return std::make_pair(occ[a[i]], i);
else occ[a[i]] = i;
}
return std::make_pair(-1, -1);
}
inline void fix_permutation(int pos)
{
static bool occ[MAXN];
for (int i = 1; i <= n; ++i) occ[i] = false;
for (int i = 0; i < n; ++i) if (i != pos) occ[a[i]] = true;
for (int i = 1; i <= n; ++i) if (!occ[i]) { a[pos] = i; return; }
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
for (int i = 0; i < n; ++i) scanf("%d", &b[i]);
std::pair<int, int> dup_a, dup_b;
dup_a = get_duplication(a);
dup_b = get_duplication(b);
if (dup_a == dup_b) {
a[dup_a.first] = b[dup_b.first];
} else if (dup_a.first == dup_b.first || dup_a.first == dup_b.second) {
a[dup_a.second] = b[dup_a.second];
fix_permutation(dup_a.first);
} else if (dup_a.second == dup_b.first || dup_a.second == dup_b.second) {
a[dup_a.first] = b[dup_a.first];
fix_permutation(dup_a.second);
} else {
a[dup_a.first] = b[dup_a.first];
a[dup_a.second] = b[dup_a.second];
}
for (int i = 0; i < n; ++i) printf("%d%c", a[i], i == n - 1 ? '\n' : ' ');
return 0;
}
#include <cstdio>
#include <algorithm>
static const int MAXN = 1502;
static const int ALPHABET = 26;
int n;
char s[MAXN];
int ans[ALPHABET][MAXN] = {{ 0 }};
int q, m_i;
char c_i;
int main()
{
scanf("%d", &n); getchar();
for (int i = 0; i < n; ++i) s[i] = getchar() — 'a';
for (char c = 0; c < ALPHABET; ++c) {
for (int i = 0; i < n; ++i) {
int replace_ct = 0;
for (int j = i; j < n; ++j) {
if (s[j] != c) ++replace_ct;
ans[c][replace_ct] = std::max(ans[c][replace_ct], j - i + 1);
}
}
for (int i = 1; i < MAXN; ++i)
ans[c][i] = std::max(ans[c][i], ans[c][i - 1]);
}
scanf("%d", &q);
for (int i = 0; i < q; ++i) {
scanf("%d %c", &m_i, &c_i);
printf("%d\n", ans[c_i - 'a'][m_i]);
}
return 0;
}
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
typedef long long int64;
static const int MAXN = 1004;
#ifndef M_PI
static const double M_PI = acos(-1.0);
#endif
int n;
int x[MAXN], y[MAXN], r[MAXN];
int par[MAXN];
std::vector<int> e[MAXN];
// Whether one of C[u] and C[v] is contained in another
inline bool circle_contains(int u, int v)
{
return ((int64)(x[u] - x[v]) * (x[u] - x[v]) + (int64)(y[u] - y[v]) * (y[u] - y[v]) <= (int64)(r[u] - r[v]) * (r[u] - r[v]));
}
int64 f[MAXN][2][2];
void dfs_dp(int u)
{
int64 g[2][2] = {{ 0 }};
for (int v : e[u]) {
dfs_dp(v);
for (int i = 0; i <= 1; ++i)
for (int j = 0; j <= 1; ++j)
g[i][j] += f[v][i][j];
}
for (int i = 0; i <= 1; ++i)
for (int j = 0; j <= 1; ++j) {
f[u][i][j] = std::max(
// (1) <u> is assigned to the first group
g[i ^ 1][j] + (int64)r[u] * r[u] * (i == 0 ? +1 : -1),
// (2) <u> is assigned to the second group
g[i][j ^ 1] + (int64)r[u] * r[u] * (j == 0 ? +1 : -1)
);
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d%d%d", &x[i], &y[i], &r[i]);
for (int i = 0; i < n; ++i) {
par[i] = -1;
for (int j = 0; j < n; ++j)
if (r[j] > r[i] && circle_contains(i, j)) {
if (par[i] == -1 || r[par[i]] > r[j]) par[i] = j;
}
e[par[i]].push_back(i);
}
int64 ans = 0;
for (int i = 0; i < n; ++i) if (par[i] == -1) {
dfs_dp(i);
ans += f[i][0][0];
}
printf("%.8lf\n", (double)ans * M_PI);
return 0;
}
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
typedef long long int64;
static const int MAXN = 1004;
#ifndef M_PI
static const double M_PI = acos(-1.0);
#endif
int n;
int x[MAXN], y[MAXN], r[MAXN];
int par[MAXN];
std::vector<int> e[MAXN];
bool level[MAXN];
// Whether one of C[u] and C[v] is contained in another
inline bool circle_contains(int u, int v)
{
return ((int64)(x[u] - x[v]) * (x[u] - x[v]) + (int64)(y[u] - y[v]) * (y[u] - y[v]) <= (int64)(r[u] - r[v]) * (r[u] - r[v]));
}
void dfs_colour(int u, bool c)
{
level[u] = c;
for (int v : e[u]) dfs_colour(v, c ^ 1);
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d%d%d", &x[i], &y[i], &r[i]);
for (int i = 0; i < n; ++i) {
par[i] = -1;
for (int j = 0; j < n; ++j)
if (r[j] > r[i] && circle_contains(i, j)) {
if (par[i] == -1 || r[par[i]] > r[j]) par[i] = j;
}
e[par[i]].push_back(i);
}
for (int i = 0; i < n; ++i) if (par[i] == -1) dfs_colour(i, false);
int64 ans = 0;
for (int i = 0; i < n; ++i)
ans += (int64)r[i] * r[i] * (par[i] == -1 || (level[i] == true) ? +1 : -1);
printf("%.8lf\n", (double)ans * M_PI);
return 0;
}
One more thing — Staying up late is bad for health.
#include <cstdio>
#include <cstring>
typedef long long int64;
static const int MAXN = 52;
static const int MODULUS = 1e9 + 7;
#define _ % MODULUS
#define __ %= MODULUS
int n, d[MAXN];
int64 f[2][MAXN][MAXN][MAXN][MAXN] = {{{{{ 0 }}}}};
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d", &d[i]);
int cur = 0, next = 1;
f[cur][d[0] == 2][d[0] == 3][d[1] == 2][d[1] == 3] = 1;
for (int i = 1; i < n - 1; ++i) {
memset(f[next], 0, sizeof f[next]);
for (int p1 = 0; p1 <= n; ++p1)
for (int p2 = 0; p1 + p2 <= n; ++p2)
for (int c1 = 0; c1 + p1 + p2 <= n; ++c1)
for (int c2 = 0; c1 + c2 + p1 + p2 <= n; ++c2) if (f[cur][p1][p2][c1][c2] > 0) {
int64 val = f[cur][p1][p2][c1][c2];
// (1) Start a new level
if (p1 == 0 && p2 == 0) {
(f[cur][c1][c2][0][0] += val)__;
continue;
}
// (2) Stay on current level
// Which type of vertex in the last level?
for (int last_level = 0; last_level <= 1; ++last_level) {
int last_ways;
if (last_level == 0) {
last_ways = p1;
if (--p1 < 0) { ++p1; continue; }
} else {
last_ways = p2;
if (--p2 < 0) { ++p2; continue; } else ++p1;
}
// Which type of vertices in the current level?
if (d[i + 1] == 2) {
// a) Leave as it is
(f[next][p1][p2][c1 + 1][c2] += val * last_ways)__;
// b) 1-plug
if (c1 >= 1)
(f[next][p1][p2][c1 - 1][c2] += val * last_ways * c1)__;
// c) 2-plug
if (c2 >= 1)
(f[next][p1][p2][c1 + 1][c2 - 1] += val * last_ways * c2)__;
} else {
// a) Leave as it is
(f[next][p1][p2][c1][c2 + 1] += val * last_ways)__;
// b) 1-plug
if (c1 >= 1)
(f[next][p1][p2][c1][c2] += val * last_ways * c1)__;
// c) 2-plug
if (c2 >= 1)
(f[next][p1][p2][c1 + 2][c2 - 1] += val * last_ways * c2)__;
// d) 1-plug + 1-plug
if (c1 >= 2)
(f[next][p1][p2][c1 - 2][c2] += val * last_ways * c1 * (c1 - 1) / 2)__;
// e) 2-plug + 2-plug
if (c2 >= 2)
(f[next][p1][p2][c1 + 2][c2 - 2] += val * last_ways * c2 * (c2 - 1) / 2)__;
// f) 1-plug + 2-plug
if (c1 >= 1 && c2 >= 1)
(f[next][p1][p2][c1][c2 - 1] += val * last_ways * c1 * c2)__;
}
if (last_level == 0) ++p1; else ++p2, --p1;
}
}
cur ^= 1, next ^= 1;
}
printf("%lld\n", f[cur][0][0][0][0]);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using D = double;
using uint = unsigned int;
template<typename T>
using pair2 = pair<T, T>;
#ifdef WIN32
#define LLD "%I64d"
#else
#define LLD "%lld"
#endif
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
const int maxn = 55;
const int MOD = 1000000007;
int ways[maxn][maxn][maxn];
int answer[maxn][maxn];
int n;
int d[maxn];
int sumd[maxn];
inline void add(int &a, ll b)
{
a = (a + b) % MOD;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &d[i]);
ways[0][0][0] = 1;
for (int c0 = 0; c0 <= n; c0++)
{
for (int c2 = 0; c2 <= n; c2++)
{
for (int c1 = 0; c1 <= n; c1++) if (c1 + c2 > 0)
{
if (c2 > 0)
{
if (c0 > 1) add(ways[c0][c1][c2], (ll)ways[c0 - 2][c1][c2 - 1] * (c0 * (c0 - 1) / 2)); // 2-0, 2-0
if (c2 > 1 && c0 > 0) add(ways[c0][c1][c2], (ll)ways[c0 - 1][c1 + 1][c2 - 2] * (c2 - 1) * c0); // 2-2, 2-0
if (c2 > 2) add(ways[c0][c1][c2], (ll)ways[c0][c1 + 2][c2 - 3] * ((c2 - 1) * (c2 - 2) / 2)); // 2-2, 2-2
if (c1 > 0 && c2 > 1) add(ways[c0][c1][c2], (ll)ways[c0][c1][c2 - 2] * c1 * (c2 - 1)); // 2-2, 2-1
if (c1 > 0 && c0 > 0) add(ways[c0][c1][c2], (ll)ways[c0 - 1][c1 - 1][c2 - 1] * c1 * c0); // 2-1, 2-0
if (c1 > 1) add(ways[c0][c1][c2], (ll)ways[c0][c1 - 2][c2 - 1] * (c1 * (c1 - 1) / 2)); // 2-1, 2-1
} else
{
if (c0 > 0) add(ways[c0][c1][c2], (ll)ways[c0 - 1][c1 - 1][c2] * c0); // 1-0
if (c1 > 1) add(ways[c0][c1][c2], (ll)ways[c0][c1 - 2][c2] * (c1 - 1)); // 1-1
}
}
}
}
for (int i = 0; i < n; i++) sumd[i + 1] = sumd[i] + d[i];
answer[n][n - 1] = 1;
for (int l = n - 1; l > 0; l--)
{
for (int r = l; r < n; r++)
{
int cnt2 = sumd[r + 1] - sumd[l] - 2 * (r - l + 1);
int cnt1 = r - l + 1 - cnt2;
for (int nextlvl = 0; nextlvl <= 2 * cnt2 + cnt1 && nextlvl <= n; nextlvl++)
{
int curways = ways[nextlvl][cnt1][cnt2];
if (r + nextlvl < n)
{
add(answer[l][r], (ll)answer[r + 1][r + nextlvl] * curways);
}
}
}
}
if (d[0] + 1 > n) cout << 0 << endl;
else cout << answer[1][d[0]] << endl;
return 0;
}
This is the round with the most solutions so far perhaps? There are at least 3 × 2 × 3 × 3 × 3 = 162 different ways to pass all problems in this round =D
Pla-tinum happy though I'm supposed to be
Pla-tinum sad is somehow how I get
Personally I'd like to express my gratitude to the community for creating this amazing first-time experience for me. Thank you, and see you next round. Probably it will be for Ha... Well, let's wait and see :)
Cheers \(^ ^)/










Thanks for fast editorial :)
Please fast rating update too :)
Bonus. Figure out why solution 2 is not hackable.
Because all permutations of b (maybe except sorted) is valid?
Seems legit. The loop will not be executed more than twice.
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
Thank you for the great problems, especially problem C and D :)
You have got 803 rating in one contest! This is the biggest change I have ever seen.
Translation: Is there any kind of operation like this? O(∩_∩)O
Problem E is awesome. I had a O(n^6) solution at the beginning and made it O(n^5) soon. Then I spent nearly an hour to optimize it. Finally I got a O(n^4) solution and the contest ended.
Anyway this problem is a really graceful dynamic programming problem in my opinion, which made me doubt whether I was solving problem in topcoder. Just an analogy, don't mind :)
Agree.
I also had an O(n^6) solution at the beginning, made it O(n^5) soon, but when I was writing the code I found that there's a useless dimension in my DP status, deleting it resulted in an O(n^4) solution...
What is the O(n^4) solution? I know an O(n^5) solution using DP state comprising of index, 2_left_in_last_level, 3_left_in_last_level, 2_left_in_current_level and 3_left_in_current_level.
It can be seen that you have to connect exactly one point left in the last level if there has one. So you just need to keep the number of points in the last level. When the current level becomes the last level, calculate the number of ways of these points connect to some points on the right (but we don't care about what these points are), which is actually equal to the number of permutation with repetition.
2_left_in_last_level and 3_left_in_last_level can be merged: remain_degrees_in_last_level = (2_left_in_last_level + 2 * 3_left_in_last_level).
In the O(n^5) solution, we multiply the answer by (2_left_in_last_level) and then decrease (2_left_in_last_level) by 1 if we choose a vertex with 1 remaining degree in last level, or multiply the answer by (3_left_in_last_level) and then decrease (3_left_in_last_level) by 1 and increase (2_left_in_last_level) by 1 if we choose a vertex with 2 remaining degrees in last level.
In fact we can precalculate the number to be multiplied when we change the level: (remain_degrees_in_last_level)! / 2^(3_left_in_last_level). (can be proved with combination knowledge)
In the O(n^4) solution, we just merge 2_left_in_last_level and 3_left_in_last_level into remain_degrees_in_last_level, and multiply the answer by (remain_degrees_in_last_level)! / 2^(3_left_in_last_level) when we change the level, no longer caring whether to choose a vertex with 1 or 2 remaining degree(s) in last level.
You did a good job :)
Thanks for your appreciation! What a pity you didn't make it > <
Actually O(n5) is one of the intended solutions, if implemented with a constant factor of 1 / 8 or lower. I also feel this problem quite TC-ish myself.
But I think memory limit is too tight for n^5 solution.
I got dp[2][2*N][2*N][N][N] and passed with 247MB.
Yes, perhaps the ML should have been larger in order to let all O(n5) solutions pass easily. But you can try some different DP that would use an f[2][N][N][N][N] array.
If it's Topcoder, you won't come up with a polynomial-time algorithm at the beginning. lol
Can you tell me how I can improve my dynamic programming skills ? I had no idea how to approach that problem at all.
Thanks.
Practice and struggle. That's all there is to life, my friend. :)
I meant some resources with easy DP problems and then building up ...
You're literally sitting on the best website for resources.
Here you go. Solve some problems, and when you start finding them easy, then skip a few. Repeat.
why is my solution got TLE ?
cyand1317
27649598
same complexity passed with many others
Your solution has a factor if I got it right, and that actually is not intended. Similar solutions will get AC or TLE depending on implementation, so next time remember to test it against maximum data :)
factor if I got it right, and that actually is not intended. Similar solutions will get AC or TLE depending on implementation, so next time remember to test it against maximum data :)
You should have let all the O(n*q) solutions pass :P
Woow
the big array size was the cause of TLE
same code .. good array size passed O.o
cyand1317
27656648
aka.Sohieb
But I am still interested in why it says your code got TLE not MLE?
anyone who completed problem c in java ?
with python3 i can not make less than 5.5s :(
Yeah you can do some precomputation and solve all cases before you take in queries (there are only n*26 different cases) and then just print out the queries as you get them. Ran in less than 500ms.
Can anyone please explain the solution for Problem — C.I am not able to understand the editorial.
Which particular part of it? Perhaps I can make it clearer.
The Preprocessing Part.What do you do for each letter?
Mm, I'm rewriting the tutorial and it will be updated soon.
Clearly, given a color c and a number of repaints m you could bash through all possible intervals and find the maximum valid substring, but this would take too long, with n(n+1)/2 possible intervals and q queries, taking O(n^2*q) time.
We can resolve this issue as there are 26n possible queries (as there are 26 letters in the alphabet and m is constrained to [1,n]. Therefore we run through every possible query and store its answer in an array Ans[c][m]. (this takes O(n^2*26) time)
To run through every possible query we look at every possible color and every single possible subinterval, and find the minimum number of recolors needed to make that interval valid. We compare the size of this interval to the size currently stored in Ans[c][r-l+1-t], and store the maximum of the two.
However, this only finds the maximum value when exactly m colors are recolored, but in some cases not all m colors need to be recolored, for example take string axaxa for favorite color a, a maximum of 2 recolors will be needed even if we have more than 2 recolors available. Therefore, for each color we iterate through [1,m] and if Ans[c][j] is less than Ans[c][j-1], we replace Ans[c][j] with Ans[c][j-1]. Using the above example, Ans[a][2] would = 5 while Ans[a][3] would = 0, and so we set Ans[a][3] to 5. (Restating what I said above: the maximum vaild substring given a number of recolors m is equal to the maximum valid substring that can be obtained by any number p such that 1<=p<=m. We originally only found answers which used exactly m recolors.)
Then we handle each query by using this 2-D array as the solutions are precomputed.
= = really nice explanation!
Problem C. Got TLE with O(nq) solution. Any idea how to fix it? http://mirror.codeforces.com/contest/814/submission/27651582
Try adding the following code lines:
I think that you got TLE because the input file is too large and cin/cout is a little bit slow without the lines above.
Bonus for C in O(nq) can be easily done using two pointers (sliding window).
Maintain a left pointer l, and a right pointer r. For current window size, let cnt be the number of characters present in the window, that are not equal to c, which is the current favourite character. Now, while cnt <= m, we can expand the window, hence we increment r, and update cnt according to the new character added to the window. Once cnt > m, we increment l (and update cnt according to the character being removed from the window), and continue the process. At each valid window, we can check it's size, and update our final answer accordingly
Check my submission for better understanding. Code
I have the same solution and interesting in if there is a guarantee about working less than 2 seconds ? I was hoping only on power of computers of the verification system. As I know, approximate number of actions per second about 100 millions. So, we have O(n * q) ~ 300 millions actions and only 2 seconds.
Though the solution with complexity O(n * q) passes, you can still optimize that solution. As m < = 1500, the total number of unique queries can be 26 * 1500(as there can be 26 different alphabets for each m). Hence the queries in the input will repeat. So you can save the answers for the queries as you encounter them, and if that query is repeated again, you can simply print it directly without solving again. You can do this by maintaining an array dp[27][1510]. Here are my submissions with and without this optimization.
Submission 1: 27657218
Submission 2: 27657190
There is a huge difference in time.
I think it's similar to O(n^2 * 26 + q) as I understand, but I'm interesting in if there are some guaratees without optomization.
I did C using Binary Search on the answer and checking whether for the particular value of answer is it possible to paint a subsegment by combining it with the sliding window. Code
Can't understand the description of E. Must the graph be a tree?
No, the second sample itself is not a tree. But if you construct the shortest path graph, that will be a tree because there is a unique shortest-path from every vertex to the capital. Apart from these edges of the tree, edges can be present between siblings nodes in the tree.
can u pls explain a bit more what the states represent here. thx
Could someone explain me a solution of problem D, please.
I solved D with Dynamic programming(memoization):
D[1111][2][2][2]: D[node][|set1|_is_odd?][|set2|_is_odd?][node_belogs_to_set2?]Then the core part becomes
D[node][odd1][odd2][at_odd2] = (odd1 && !at_odd2) || (odd2 && at_odd2) ? area[node]: -area[node] + get_optimal_combination(direct_children[node])Here,
direct_childrenconsists of literally indices of direct children, which means, for eachyindirect_children[node], there is no other circle smaller thannodewhich is parent ofy.And
get_optimal_combinationis simple, too: this is just a sum ofmax(D[child][!odd1][odd2][false], D[child][odd1][!odd2][true]);(this is obvious so that I will omit the proof).Code here: http://mirror.codeforces.com/contest/814/submission/27661135
P.S. I think this problem can solved using plain DFS without DP.
If we define the level of a circle as the number of circles that completely enclose it, then for any circle, its effective area can be seen as sum of all the even levels minus the sum of all the odd levels. My solution was to move to the second plane all circles whose level is 1, that is, all the circles that have exactly one circle enclosing them. It's pretty easy to see why this works, but let me know if you need a proof. 27655767
Could you please give a proof? Thanks a lot.
In test case 6 of problem B:
10
1 2 3 4 5 6 7 8 4 10
1 2 3 4 5 6 7 6 9 10
my output is :
1 2 3 4 5 6 7 6 4 10Jury's answer was :
1 2 3 4 5 6 7 8 9 10But the problem says,it satisfies any permutations maintaing (n-1) matches..I can't find any errors with my output.It would be very helpful if someone helps me with my confusion.Thanks in advance.
@TajirHas9 the answer should be a permutation of 1,2,3....n .Read the problem statement again!
Thank you very much.I noticed that now.I thought any permutation is acceptable.But problem statement says 1 to n inclusive indeed. :(
I can't understand how spaciousness is defined in problem D?Is it unique for given set of circles.How are those odd ranges chosen?P
The spaciousness is the total area that is covered by an odd number of dancers. So, for example, if a region is covered by only one dancer, this region is included in the computation of total spaciousness, if a region is covered by exactly two dancers, it is not.
Your goal in the problem is to maximize the total spaciousness by allocating some dancers to dance only after midnight and some to dance only before midnight.
c problem .....in the editorial code->what is the use of this loop:-
isn't
for (int i = 1; i < MAXN; ++i) ans[c][i] = std::max(ans[c][i], ans[c][i - 1]);The mean of
ans[c][i]: the best ans when exactly change i times.You can not change so many times with string :
aaaaaaaaaand query4 aSo that you should get a prefix max。
I don't understand what is this "26" in the editorial of problem C
You have to precompute for each possible color, and there are 26 alphabets so 26 possible colors.
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
Can anybody explain how the tree structure in problem D can be built in O(n log n) ?
Using BST and scanning line.
First we divide each circle into two arcs,the upper one and the lower one.Then process all arcs from left to right,inserting and deleting arcs in the BST.
In the BST we sort the arc by vertical order.(As no circles intersect,each pair of arcs can be compared vertically).
When we insert an upper arc,we can find the closest arc which is on top of it. If the closest arc which is on top of it is an upper arc,then the closest arc is the parent of the arc being inserted.Otherwise,we find a lower arc or no arc at all.If no arc at all,the arc being inserted can't be contained by any other circle.If a lower arc is found,this lower arc should have the same parent as the arc being inserted.
There're some computational geomatry problems employing this technique in Chinese OI.
Poor English,a better explanation is needed.
Notice that we have n ≤ 1000, so using O(n2) brute force is already enough.
Oops, didn't notice that we're talking about the solution. I won't be so careless again.
solution. I won't be so careless again.
Thank you for your explanation.
would u like to explain how to deal with two circles are tangent with each other?
I'm struggling to get your solution correct...
After replacing the DP part with my AC code and some changes to the cmp() function it now get WrongAnswer on test 27 http://mirror.codeforces.com/contest/814/submission/27671766
Still trying now.
ah i am really appreciate that, i realize the reason i got wrong answer may because of my original wrong dp... >>
i think that, coz i build a virtual node, so maybe u have to count in another way, like ans += f[0][0][son] if(x is n+1)
anyway, cheers
http://mirror.codeforces.com/contest/814/submission/27672108 Accepted now. Some changes to "operator <" were added in this version.
When compare arcs,we use "upper" "lower" in the straightforward meaning:whether they seems upper/lower
wow nice one :)
danks!
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
Is problem C a form of a classic DP problem??
Ah ha~~~ What do you mean by using 'Let's wait and see." ~ ^_^
Is problem C a form of a classic DP problem??
I think it's quite classic. It's not DP but preprocessing + sliding-window method actually, though the memorizations are a bit alike.
can you tell me the name of the classical problem which is similar to that problem??
I mean, this technique is similar to DP, though it isn't. There are quite a few DP problems on strings out there but I can't think of one right now. Perhaps someone else might help.
I think the most classical idea in this problem is "noticing" you are dealing with an alphabet with 26 letters, so you can preprocess individually. Exploring this idea is useful for a handful of problems that have different approaches. Even tries would not have the same complexity if your alphabet was greater. You could find a longest non decreasing subsequence of characters in O(26*n), as another example.
I couldn't understand DP on trees for problem D.Can someone explain a bit more on that DP part?
Thanks in advance and sorry if the question seemed to be trivial.
how could u construct the tree for D in ?
?
particularly plz specific how to deal with two circles tangent with each other.
coz i used sweepline + set which leads to Wrong answer on 4 >.<
I the same WA on testcase 6
wa on case 6 may be the wrong idea with dp >>
what i did is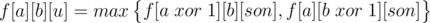 for each i's son
for each i's son
but it is wrong, we should count his brothers in
which should be
and then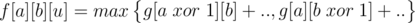
hmm, exactly the same as the solution.
Thank U all the same though I use greedy algorithm... I was considering that methods discussed above by liu_runda is too complicated Maybe we could only deal with upper arcs (Keep trying...
ah okay, for that one, u can draw two graphs, if the one with shorter distance to it is upper arcs, the current circle we are looking at, is contained by the circle which the particular upper arcs belongs to.On the other hand, if it is a lower arcs, they must have the same situation, which means they are brothers.
I don't understand the formular f[u][0/1][0/1] of D's solution. What does it mean?
Let F[u][isOddGroup1][isOddGroup2] be the best sum for distributing the circles between first group and second group optimally, so you can either make the circle u in the first group or the second group, and either sum or subtract the circle u area according to the parameters isOddGroup1 and isOddGroup2 respectively.
so the result of the tree root u should be max(f[u][0/1][0/1])?
f[u][p1][p2] is the maximum total answer in the subtree of u, assuming there are p1 nodes assigned to the first group and p2 nodes assigned to the second group among u's ancestors. And we only need to care about the oddness/evenness of p1 and p2 so we store them modulo 2.
Edit: Seems I was a bit too slow XD
For a node u, we look at its ancestor, that's clear. What's not clear is why we use u's subtree to calculate f instead of its ancestors. The provided solution does exactly that, doesn't it?
In the editorial, p1 and p2 are kind of assumed. So f means "what's the best we can get in the subtree, if the ancestors are in this state." We calculate this value bottom-up, and u's value will be used by its parent.
Other approaches may not use ideas like this, though.
Can any one guide me how to do Problem c with top down dp approach.I have written the recursive implementation but i am unable to memoize ,that's why i am getting tle.Thanks in Advance.
Here is my solution link
Here is my top down code. I think it is self explanatory.
In problem E, why can't we club p1 and p2, and club c1 and c2, and have dp[u][p1 + 2*p2][c1 + 2*c2], which denotes number of ways to build the graph with the first u vertices, with (p1 + 2*p2) plugs in the previous level, and (c1 + 2*c2) in the current one?
Because then you could pair two nodes twice, which is not permitted.
why title of C and E is not English?
Hello,
what do we mean by Figure out why solution 2 is not hackable.
what is the meaning of hackable and why is not hackable.
is the solution 1 hackable?
Solution 2 seems to have a complexity of O(k!*n). (though it's O(n+k) indeed)
Both solution 1 and 2 are correct (not hackable).
Can you please explain the general idea of the second solution?
This problem asks us to "detect whether it is possible to replace each zero in a with an integer from b so that each integer from b is used exactly once, and the resulting sequence is not increasing".
The second solution is just a simple idea: to try every way to "replace each zero in a with an integer from b so that each integer from b is used exactly once", and then check if "the resulting sequence is not increasing".
As this comment said, "all permutations of b (maybe except sorted) is valid". So the O(k!) loop will
break;in O(1).In problem D I can't understand this statement " consider a vertex u, and the parity (oddness/evenness) of number of nodes in its ancestors from the first and the second group."
in this matrix f[u][0/1][0/1] what represent the second and the third dimension I didn't get it
thank you in advance
You can solve D with pure DFS, no DP needed.
for every tree, Add the root to the first group, and the the children of the root to the second group , so answer = Area of Root + Area of each of the root's children, after that either add the area of the current circle to the total answer if the depth is even , or subtract the area if the depth is odd.
This works because, if The maximum depth of the tree is 2, it is optimal to put the root on one side and the root's children on the other side,then you simply add all the areas to the final answer,but if you add another smaller circle into the plane, you increase the depth by one so this new circle area will definitely get subtracted if put on any side,we solve this by adding its children(which have depth4) inside it(to decrease the loss of area),then same goes for circle of depth 5 and its children.
http://mirror.codeforces.com/contest/814/submission/27689113
Is the explication given by Karemm_Mohamed false??
why many people dislike his answer?
Can you explain for me how to dp array WAYS of solution n ^ 3 in problems E.
I don't understand how it work and remarks in code such as // 2-0, 2-0 // 2-2, 2-0 .... etc !
Just a rough idea for understanding the sample solution: consider what happens when we add edges among vertices of the same level (with c1 "1-plug" vertices and c2 "2-plug" ones), and from a vertex in that level to a vertex in a new level (with c0 vertices). "Plugs" of certain vertices will decrease (some "2-plug" vertices become "1-plug" for example), depending on the edges we choose.
We take a vertex and consider how they're connected to other vertices. The comments are in the form of "(the vertex we're currently considering) — (the vertex it's connected to)". e.g. "2-1, 2-0" means we take a "2-plug" vertex and connect it to a "1-plug" vertex in its own level and a vertex in the new level (denoted by 0). We can choose different vertices of the same "plugs" to connect to, so previous DP values are multiplied by number of such ways, like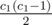 .
.
Thanks for your help. I understood !
Can someone explain their greedy solutions for D with proof of correctness ?
The comment above by Kareem_Mohamed is a common one FYI (basically it's explaining exactly Solution 2 in the tutorial, I don't know why it's downvoted :/). I've seen a few approaches equivalent to this, but I'm also curious whether someone came up with other insights and ended up in the same solution.
Above all thanks for the great DP round. XD
Here is one question. For problem E's sample O(n3) solution, there is a part of constructing from subproblem which says
"if (c2 > 2) add(ways[c0][c1][c2], (ll)ways[c0][c1 + 2][c2 — 3] * ((c2 — 1) * (c2 — 2) / 2)); // 2-2, 2-2"
As c1, c2, c0 are all limited under 50. How can we guarantee we always have future information [c1 + 2] when we need to calculate f[c0][c1][c2]? For example, when calculating f[1][49][30], we don't have the memo of f[1][51][27] cause c1 is larger than 50.
For indices larger than 50 the corresponding DP values are all 0 due to implicit array initialization. And note that DP values are calculated in c0-c2-c1 order so we can be sure the values we need at some time are all calculated before.
Well, I got this one, thank you!
Would you pls give me a hint on how to set the initial value for ans[n][n — 1] = 1. Is there any physical meaning for this?
There is one way to build a graph with vertices numbered between n and n - 1 — "no vertices", and "no vertices" form the first level, that is, zero edges from the previous level need to be connected to it.
cyand1317 could you explain the dp states in D?
For a node u, does f[u][0][0] mean that u belongs to the first group and has depth%2 = 0?
This comment FYI :)
I got an easy greedy solution for Problem D. Pretty straight forward 20 (actual) lines of code.
Submission
Basically take circles in decreasing order of radius. Find its immediate encompassing-circle. Then depending on the "tag" of that parent-circle, assign the "tag" for the current circle. Then add certain values of "tags".
Essentially I skipped the trees. And Dfs.
I'm having trouble understanding the problem D and it's example test cases. what does the area covered by an odd number of movement ranges of dancers who are moving. actually mean? how exactly is spaciousness calculated??
How would you do the bonus for problem D?