Здравствуйте!
Допустим, есть множество из n элементов a1, ..., an, на котором введено отношение частичного порядка < , притом у нас есть оракул, который позволяет узнать: верно ли, что ai < aj. Необходимо отсортировать данные элементы, то есть найти такую перестановку b1, ..., bn, что не найдётся i < j таких, что bj < bi.
Хочется минимизировать количество обращений к оракулу. Понятно, что можно сделать O(n2) обращений, используя топологическую сортировку. Но можно ли делать это быстрее? Если нет, то интересно узнать доказательство этого.










Предположим, что нам всегда дают массив, в котором только одна пара элементов сравнима. Тогда чтобы посортировать нам надо найти эту пару и вроде нельзя это сделать быстро
Как сказал riadwaw, отсортировать общую последовательность быстрее нельзя — но если из любых двух элементов один больший другого, то восможно найти перестановку с bi + 1 > bi для всех i (путь длины N в графе ответов оракула) на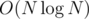 обращений. При этом восможно что корректно отсортированая перестановка не сучествует.
обращений. При этом восможно что корректно отсортированая перестановка не сучествует.
Если из любых двух элементов один больше другого, то нам задан линейный порядок и мы можем любым алгоритмом сортировки воспользоваться. Или я что-то не так понял?
А как для любого алгоритма сортировки без использования графов понять, что не существует правильной перестановки. Например: b1 < b2, b2 < b3, b3 < b1 . Сделать еще n запросов?
А это опять же, кажется, быстро не получится. Предположим, что всегда, кроме одной пары
всегда, кроме одной пары