x = 0;
while(x < 1){
y = x;
x += rand(); // returns a real number between 0 and 1, uniformly at random
}
What is the expected value of y?
It's not very hard, but the result is surprising.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
x = 0;
while(x < 1){
y = x;
x += rand(); // returns a real number between 0 and 1, uniformly at random
}
What is the expected value of y?
It's not very hard, but the result is surprising.
| Name |
|---|



E(y) = Sum(n = 1 ~ inf) Integrate(x = [0, 1]) ((Probability that value is x in nth iteration, and >=1 in (n+1)th iteration)xdx)
Probability density function for x in 1th iteration is 1.0
pdf for x in 2nd iteration is x / 1! (integrate above in [0, x])
pdf for x in 3rd iteration is x^2 / 2! (integrate above in [0, x])
pdf for x in 4th iteration is x^3 / 3! (integrate above in [0, x])
pdf for x in nth iteration is x^(n-1) / (n-1)!
So, E(y) = Sum(n = 1 ~ inf) n(n+1) / (n+2)! . I don't know taylor expansion, but hopefully WolframAlpha knew that. So I found E(y) = e-2.
I also thought about it that way :). You can note that if we change order of summation (meaning, sum by n and integral by x) we get that result is an integral from 0 to 1 from exx2 what equals e-2
https://www.quora.com/A-machine-outputs-random-real-numbers-between-0-and-1-until-their-sum-exceeds-1-How-many-numbers-will-it-need-to-generate-on-average/answer/Alon-Amit?srid=dE6P
For some 0 ≤ t ≤ 1, let f(t) be the answer if the loop were while(x < t) instead of while(x < 1). Clearly, f(0) = 0
We can say that :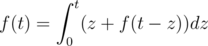
If we differentiate, then we get a differential equation f'(t) = t + f(t)
And the solution is f(t) = et - t - 1
So, f(1) = e - 2
But I don't see why this is strange?
f(0) = undefined behaviour :D
Could you explain why? The way I see it f(0) = 0 is a perfectly fine statement to make.
Because the initial value of y isn't specified.
Nope,
xis assigned to zero before the loop. Not sure if it was there 13 hours ago, though.But we are interested in value of y (not x) and code doesn't enter loop even once
Oh, right. I'm sorry.
Suppose that we have N independent random variables X_i with a continuous uniform distribution on the interval [0, 1]. What is the expected value of
min (abs (x_i-x_j))?Ps. This is weakly related to the discussion, sorry
It was posed on MSU contest on Petrozavodsk Winter 16. However proof is not easy, probably going through some integrals.
I searched answer by a randomize algorithm and I made distribution of each time's result of y.
I think the distribution of y is both surprising.
I calculated 1,000,000 times in this code:
The link of my code is here.
My code counts the number of times every 0.01 period in range [0, 1).
I used random in 64-bit integer, but 64-bit integer has over 1018 numbers so I think this method is almost real-number random.
I expected the distribution graph draws ax2 graph, but it is little-bit different. I impressed about this.
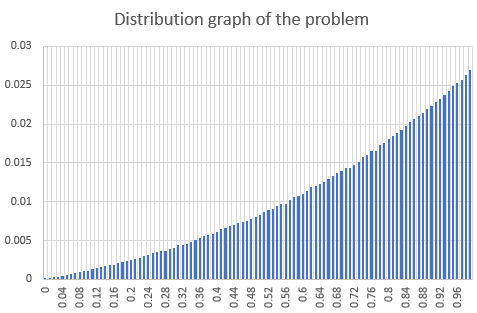
The expected value of this experiment is about 0.71806197, and this is almost e - 2.