red_coder's blog

Codeforces Round #137(Div 2) Problem E
By red_coder, 12 years ago, In English

Can anyone tell me how to solve this Problem using matrix, DP solution for this problem is too slow O(n*m*m) (n<=10^15). There exists a solution of O(m*m*m*logn) using matrix exponentiation. Can anyone please explain in detail how to solve this problem using matrix exponentiation!!!

  • Vote: I like it
  • -2
  • Vote: I do not like it

»
12 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

We can build a graph, when edge (u, v) exists, only if pair (u, v) is not forbidden. Then we need to calculate a number of paths length of N from U to V for all (U, V) from 1 to M.

This problem we can solve using matrix exponentiation. We take the adjacency matrix and raise it to the power N — 1 (using binpow, of course) , then take sum of all elements in matrix. This will be the answer to the problem. You can see my code in submissions.

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    i didnt get u completely, how to create that adjacency matrix

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it

      We have a matrix A of size M x M. A[i][j] = 1, only if the pair of symbols (i, j) is not forbidden from the input.

      Sample :

      3 3 2
ab
ba

      Here we have forbidden pairs (a , b) and (b, a) and M is 3 so we have such matrix :

      1 0 1
0 1 1
1 1 1

      Where A[i][j] = 0 for (a, b) and (b, a). 'a' is the first row in matrix, 'b' second, and 'c' third. So, that is how it looks.

      → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You build adjacency matrix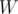 , where 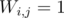if and only if pair is not forbidden, so you just assign 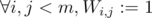. And then for each string in the input you assign 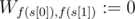, where 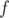is a mapping function .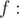

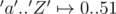      → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    why raising the adjacency matrix to power N gives us the number of paths?

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      For N = 1 answer is obvious — it's a adjacency matrix. Let's guess, that we have answer for some k, ans now we will calc answer for k + 1. We have such obvious formula : 

      d1 - answer matrix for k + 1, d - answer for k, g - adjacency matrix.
d1[i][j] = d1[i][j] + d[i][p] * g[p][j], for all p from 1 to M.

      We can notice, that this formula is matrix multiplication :

      d1 = d * g.

So, formula for any k - 

dk = g * g * g ... * g (k times).

      We can raise adjacency matrix g to power of N and get the answer. I don't know TeX, sorry.

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Thanks.

        → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        i didnt get this line- d1[i][j] = d1[i][j] + d[i][p] * g[p][j], for all p from 1 to M.

        pls explain this.....

        → Reply
        • »
          »
          »
          »
          »
          12 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          We need a path with length K + 1, we have a path length of K, so we need one single edge to complete path. 

          d[i][p] * g[p][j]

This means, number of paths length of K (i -> p) we multiply with 1 whether there are an edge from (p, j), so if there is such edge, we can complete the path with that edge - just add it to the path (i -> p) and get path (i -> j) with length K + 1. To calculate all the paths (i -> j) with length K + 1, we need to sum all this paths (i -> p -> j). Some pseudocode :

for i = 1 to m
    for j = 1 to m
        d1[i][j] = 0;
        
        for p = 1 to m
            d1[i][j] = (d1[i][j] + d[i][p] * g[p][j]) % 1000000007;

          To completely solve the problem, we need raise to the power of N — 1 the adjacency matrix and get sum of all elements in it.


          ans = binpow (g, n - 1);
for i = 1 to m
    for j = 1 to m
        answer = (answer + ans[i][j]) % 10000000007

print (answer)

          Sorry for my bad endlish)

          → Reply
          • »
            »
            »
            »
            »
            »
            12 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            excellent explanation and your english is not so bad. But one last question, i heard the name of binpow() first time. Can u give me some link from where i can read about this function like whats its return type etc..... :)

            → Reply