A. Будем идти сверху вниз и восстанавливать ответ. Нижнюю грань 1й кости восстановить легко. Далее по двум граням 2й кости можно установить какая пара чисел должна быть на верхней и нижней грани. Если одно из чисел совпадает с числов на нижней грани 1й кости, то 2я кость восстанавливается однозначно, и так далее. Если мы смогли восстановить все кости — выводим YES. Если где то возникла неоднозначность, то можно показать, что эта однозначность будет сохраняться и для всех последующих костей. То есть получится хотя бы 2 разничных ответа, поэтому нужно выводить NO.
Автор — Ripatti .
B. Сначала сгенерируем все числа k-боначчи, не превышающие n. Для k ≤ 32 это можно сделать в лоб, а для больших k можно заметить, что числа k-боначчи до 109 являются только степени двойки (и еще 0). Итого получим не более 100 чисел.
Далее предлагается действовать жадно — отнимать от n самое большое число k-боначчи, не превышающее n до тех пор, пока не разложим полностью.
Почему все полученные числа будут различны? Вот одно из возможных доказательств:
F(k, n) = F(k, n - 1) + F(k, n - 2) + ... + F(k, n - k)
F(k, n - 1) = F(k, n - 2) + F(k, n - 3) + ... + F(k, n - k - 1)
Вычтеми из 1го равенства 2е и получим F(k, n) + F(k, n - k - 1) = 2F(k, n - 1), то есть 2F(k, n - 1) ≥ F(k, n). Это неравенство так же справедливо и для n ≤ k.
теперь предположим, что жадный алгоритм даст 2 одинаковых числа F(k, x) в разложении. Но тогда, в силу неравенства, мы должны были взять число F(k, x + 1). Противоречие.
Впрочем, доказывать это не требовалось, можно было просто поверить что жадность пройдет:)
C. Сначала посчитаем число белых и черных пикселов в каждом столбике. После этого посчитаем сумму черных и белых пикселов на каждом префиксе в последовательности столбиков. Это позволит нам за O(1) вычислять количество черных и белых пикселов на любом отрезке столбиков.
Далее воспользуемся динамическим программированием. dp[i][j] будет хранить наименьшее число перекрашиваемых пикселов на префиксе от 1го столбика до j-го, причем цвет последней полосы будет белым для i = 0 и черным для i = 1.
Далее dp пересчитывается следующим образом: dp[0][0] = dp[1][0] = 0 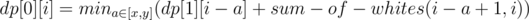
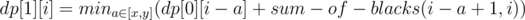
Ответом будет min(dp[0][m], dp[1][m]).
Итого решение за O(nm + m * (y - x)).
Автор — Ripatti .
D. Обычный поиск в ширину. Состояние — положение головы + маска, которая задает положение хвоста, а именно: двумя битами кодируется относительное положение каждого сегмента (кроме головы) относительно предыдущего. Итого в маске максимум 16 бит, оценка на общее число состояний — 48 × 15 × 15 (на самом деле можно даже показать оценку порядка 38 × 15 × 15).
Далее нужно просто все очень аккуратно реализовать.
Автор — Ripatti .
E. Дано: z = [x / 2] + y + xy. Это равносильно
z = [2k / 2] + y + 2ky, где x = 2k, k > 0
или
z = [(2k + 1) / 2] + y + (2k + 1)y, где x = 2k + 1, k ≥ 0.
Преобразуем:
z = k + y + 2ky, k > 0
или
z = k + y + (2k + 1)y, k ≥ 0.
Еще пару шагов:
2z + 1 = 2k + 2y + 4ky + 1, k > 0
или
z + 1 = k + 2y + 2ky + 1, k ≥ 0.
2z + 1 = (2k + 1)(2y + 1), k > 0
или
z + 1 = (2y + 1)(k + 1), k ≥ 0.
Из второго уравнения видно, что z должно быть вида 2t - 1, иначе z + 1 имеет нечетный делитель и мы можем подобрать решение. Из первого же уравнения получаем, что 2t + 1 - 1 должно быть простым, иначе опять можно подобрать решение. Если же z = 2t - 1, а 2t + 1 - 1 — простое, то очевидно, что уравнение неразрешимо.
Простые числа вида 2a - 1 являются простыми числами Мерсенна, на данный момент найдено всего 46 чисел такого вида. Показатели степени для первых 40 из них можно найти, например, здесь.
Автор — Ripatti .











Заминусовали разбор. Видимо, всем не понравились задачи.
UPD. Уже не актуально.
Мне всё понравилось, кроме Е. Задача на гугление -- не круто.
Задачи ОЧЕНЬ понравились. Главное, что было нужно, — не делать глупых ошибок. А, так как я их делаю почти в каждом контесте, я допустил багу и в этом((
Полностью согласен с yarrr. А так контест прикольный)
Ripatti, хватит создавать аккаунты и плюсовать себя с них!
o O
Мне от интересно решая В я вспомнил про "банкомат" и что не любую сумму можно выдать жадно. А как тут, без влияния луны, понять что жадность работает? Очень интересно!!!
(Для чисел Фиббоначи => жадность работает, для k>30 получаем степени двойки => жадность работает ) => Жадность работает :-)
Масло масляное
Без влияния Луны выходит как-то так:
Сначала можно показать, что любое нат. число представимо в виде суммы нескольких чисел k-боначчи.
Показывается это индукцией. База очевидна. Пусть это утверждение выполняется для всех целых чисел до f(n) (рассуждение верно для любых k>1, так что его я не пишу). Очевидно, что f(n+1)<=2*f(n) (ведь f(k,n+1)=2*f(k,n)-f(k,n-k) для n>k+2, и f(k,n+1)=2*f(k,n) для n<=k+2). Тогда для любого целого x: f(n)<x<f(n+1) верно, что x-f(n)<f(n+1)-f(n)<=2*f(n)-f(n)=f(n), т.е. представимо в виде суммы таких чисел. А, значит, и x=f(n)+(x-f(n)) также представимо в необх. виде.
Ну а дальше очевидно. Если отнять от x макс. f(k,n): f(k,n)<=x, то полученное число также представимо в виду суммы чисел k-боначчи. Плюс в разборе уже было показано, что все слагаемые будут различными.
кажется первую часть можно проще доказать:) n=1+1+...+1
Кажется, по условию, числа должны были быть различными. Я просто некорректно сформулировал утверждение, которое доказывал.
Из того, что все числа просто так представимы, еще не следует, что можно спокойно писать жадность.
жадность всегда найдет какой-то ответ (возможно с одинаковыми числами), потому что среди чисел есть 1.
6 тест 225D - Змейка
а где голова змейки?
Возможно, последняя строчка — это знак "тест вот тут обрезан" и нам не видно конец теста.
@yeputons can you please clear the problem E(unsolvable) 2 z + 1 = 2 k 2 + y + 4 KY + 1, k > 0 and and z = 1 + k 2 + y 2 + KY + 1, k ≥ 0 . how this line comes ??
6й тест такой:
просто система при показе "обрубает" длинные тесты и ставит в конце многоточие.
Для C можно было написать динамику с бОльшей памятью и временем работы, но, как мне кажется, проще в исполнении: Динамика трехмерная dp[color][j][i] — минимальное количество перекрашиваний для состояния: j — число столбцов, включая текущий с цветом color (0 — белый, 1 — черный), i — номер текущего столбца. mas[i] — число перекрашиваний для i-того столбца, чтобы превратить его в белый, очевидно, отсюда: n-mas[i] — число перекрашивай для i-того столбца, чтобы превратить его целиком в черный.
Переходы: для каждого i-того столбца: если перекрашиваем в белый цвет: dp[0][j][i] = dp[0][j-1][i-1], 2 <= j <= min(y,i+1) (т.е. идем на увеличение количества белых столбцов), и dp[0][1][i] = { x <= j <= y } min(dp[1][j][i-1] + mas[i]) — здесь мы меняем цвет столбца, если это возможно (в предыдущей последовательности черных столбцов было j: x <= j <= y). Аналогичный переход, если мы захотим красить текущий столбец в черный цвет.
Ответ, очевидно, {x <= j <= y}min(dp[color][j][m]) — берем все значения для тех состояний, когда последние j столбцов были цвета color.
Асимптотика: O(n*m)
но не нужно, та что в разборе попроще будет, да и памяти меньше
Спасибо за проблемсет, интересный вышел. Только вот не понимаю, зачем давать задачу на "погуглим". На олимпиаде такое не прокатит.
Так и не понял, какая в задаче А может быть неоднозначность: по-моему, ее либо можно восстановить единственным способом, либо такой башни вообще не существует. На каждом шаге нам известная верхняя грань t. По ней однозначна нижняя грань (7-t). Известны две боковые a[i] и b[i]. Если числа t, 7-t, a[i], b[i] попарно разные, то идем на следующий шаг, иначе — "NO", т.к. противоречие условию. На следующем шаге t = 7-t, т.к. по условию кости соприкасаются одинаковыми гранями. Можно пример входных данных, когда два варианта восстановления?
по условию кости соприкасаются разными гранями
Хх...задача Е была мне по силам, на Теорию чисел, составил ряд показателей степеней двойки, но про числа Мерсена не додумался.
Задача В, эхх как же ты меня подвела) вот как же так было забыть про то что дальше одни степени двойки пойдут? В детстве на эти же вилы наступал) http://article-factory.ru/fokusy/obuchenie-fokusam/790-volshebnaja-tablica.html
Можно было и не додумываться до этого. Можно было додуматься до того, что чем больше K, тем быстрее растут члены последовательности. А считать очередной элемент можно используя префикс-суммы. Очередная левая граница будет max(0, i — k). То есть первому члену в программе соответствует К-ый(т.е. 1). А до него все нули.
Вопрос про задачу E. 40-е число Мерсенна (2^20996011)-1 по модулю (10^9)+7 будет 395976712. Почему в 40-вом тесте ожидается 697988359?
Вам нужно 2 возносить в степень 20996010
В задаче С разве не
dp[0][i] = [x,y]min(dp[1][i-j] + sum-of-black[i-j+1, i])
dp[1][i] = [x,y]min(dp[0][i-j] + sum-of-white[i-j+1, i])
Кстати, на олимпиаде я запутался вот с этим. Но на самом деле разницы вообще никакой, так как тут главное, чтобы было dp[c][i] = min(dp[c ^ 1][i] ... ). А хотя это вполне очевидно, ведь в конце всё равно берется минимум из двух величин dp[0][n], dp[1][n]. Так кто мешает предположить, что 0 = 1, 1 = 0. Простите, если непонятно изложил свою мысль.
about D,i have other solution,easy to implement. just do it as normal BFS first , and we can think now the snake adjust it's head. After adjustments , snake can go to the @ directly ans at this time we think it's tails as wall. In fact i use force to find 100,000 states first , and from every states i use another bfs to let snake try to eat food.
In problem D, I understood that using 2 bits we can encode that how can we get from a previous position to new position. 2 bits are used to represent whether the head moves left, right, forward. Next thing we need to encode in state is representation of present position of snake which I guess is done by mask. I couldn't understand how can we represent the mask using 16 bits.
We can use mask to describe the position of i-th segment of snake relative to the i-1-th segment(for example,0 for left, 1 for down, 2 for right and 3 for up.) There are at most 9 segments, we need to encode 8 of them. That's why we need 16 bits. After making such mask, you can go through all 4 directions and find, which mask we'll have after moving to this direction.
У меня на таком тесте
валится, должно 99 у меня -1, помогите.
Реально ли решать задачи типа C без использования динамического программирования (и других чуждых для меня вещей), просто опираясь на какую либо идею и логику?
Динамическое программирование — это как раз и есть идея, а не какой-то конкретный алгоритм. Идея в том, что при поиске ответа, разбивать задачу на подзадачи, и решать её последовательно, при этом на каждом шаге использовать результат полученный на предыдущих шагах. Соответственно до этой идеи можно додуматься, и я уверен, что вы уже не раз использовали ДП, даже не подозревая о том, что это ДП =) Но когда знаешь про этот инструмент, и есть опыт его использования, то, очевидно, начинаешь быстрее понимать как и где его нужно применить.
В данном примере же идея такова: мы находим сначала ответ для одного столбика, потом для двух, для трёх и тд., пока не получим ответ для всей исходной матрицы.
У меня проблема именно в том, что я пытаюсь придумать алгоритм, который будет находить оптимальное решение. Но всегда хочется понять, почему алгоритм работает оптимально. Пока в решении, описанном в разборе, я не могу уловить эту нотку оптимальности.
Вот есть текущая позиция. Для неё мы переберём все возможные полосы, которые будут заканчиваться в этой текущей позиции. И из всех этих вариантов выберем с минимальным ответом. Так мы получим оптимальный ответ для текущей позиции. А когда последняя позиция станет текущей, то соответственно и для неё.
"Далее предлагается действовать жадно — отнимать от n самое большое число k-боначчи, не превышающее n до тех пор, пока не разложим полностью." Можете продемонстрировать на небольшом примере,а то не совсем понятно как это сделать
Здравствуйте. Добавлю, что мне вообще разбор и даже условие задачи B,похоже, совсем не понятно. Сказано, что все числа к-боначчи есть степени двойки, но в ответах есть и отличные.На 5 2 ответ 0 2 3?? Заранее спасибо.
Сказано, что для больших k k-боначчи есть степени двойки, т. е. фактически текущее число есть сумма всех предыдущих.
0 0 ... 0 1 1 2 4 8 16 ...My english is very bad and i can't understand what the author means when he says in the solution of the problem C :"After that you should calculate number of white and black pixels for every prefix in sequence of columns." What does he mean for prefix? =(
Prefix means number of first elements, i.e one of prefixes for string "abcahkjdf" is "abc"
You can solve problem B using binary search.
There are 47 mersenne primes dicovered not only 46!
http://mathworld.wolfram.com/news/2009-06-07/mersenne-47/
For problem B, is there any proof why greedy works?
Also, do you understand, why there should be only 100 numbers at max?
Can anybody guide me, I am not able to pass test case #14 of DIV2 C. Here is my solution...
My submission
Can anyone explain me how we are ensuring that no column is less then x size in problem statement C ? I got AC however it was calculating for vertical lines being less than x but I am unable to understand how it is ensured.