Dear wise-and-all-knowing people of Codeforces, I have come to call on you for aid.
I'm trying to wrap my head around rerooting an Euler tour tree. In particular, I want to be able to still do link/cut operations. I can find some bits information about rerooting on the internet (which I understand), but I don't understand how I can continue using my Euler tour tree afterwards. Thus my question is: how, if possible at all, can I use Euler tour trees to support the operations cut(u), link(u, v) (assuming u has no parent), findroot(u) and makeroot(u), each in  time? (or optionally with some extra
time? (or optionally with some extra 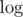 -factors) In particular,
-factors) In particular, makeroot(u) would preserve the general shape of the tree, i.e. you can't do attach(findroot(u), v)), instead all edges on the path from u to the root would be reversed.
Throughout this post let me use the left tree in this image as an example, with Euler tour 124252131. (these are the vertices in visited order, technically an Euler tour would yield the edges, but these two definitions are really equivalent, and I find this one easier to work with when doing link/cut operations)
Now, the problem comes from the fact that if you want to do e.g. a cut(u) operation, you need to cut out the segment from the first occurrence of u to its last occurrence. I.e. suppose we want to cut 2, then you get: 124252131 → 1 [24252] 131 → 24252 131 (removing a redundant 1 in front of the 2-subsequence). Note that we really need the first and last occurrence, the middle 2 is useless. If all you are doing is moving around complete segments, then the relative order of occurrences of the same vertex never changes, so you can just keep pointers to them for when you need them.
Then, rerooting. Since information about this is sparse on the internet, let me give a quick description. All that needs to be done is to rotate the sequence, with a small caveat wrt to the fact that the root of the tree appears one extra time at the end of the sequence. The algorithm is as follows:
- remove the last occurrence of the old root from the sequence (at the end of the sequence, by definition)
- rotate sequence so the first occurrence of the new root is at the front
- append the new root to the end
So suppose we reroot the example tree at 5, then we get 124252131 → 12425213 (..1) → 1242 5213 → 5213 1242 (5..) → 521312425. Done. It seems a bit magical, but basically the idea behind this is that the sequence represents a cycle (namely, the Euler tour), and hence rotating the sequence just changes the starting vertex of the tour.
But then comes the problem. All the slides I found about this (e.g. here, slide 18) just call it quits at this point. But note that this rotation screwed up the first and last for some vertices (specifically, precisely for the vertices on the path from the new root to the old root, inclusive). In fact, any of the deg(u) or deg(u) + 1 occurrences of u might be the new first or last for a vertex. Since both the number of vertices on the path between the two roots, and the degrees of these vertices (~#occurrences) can potentially be linear in n, there is no way that we can quickly recompute first and last, i.e. we probably have to compute this information lazily. But I have no idea how to do this. And yet we really need these occurrences to quickly detach a subtree (or answer the query "is u an ancestor of v" or whatever).
Please send help.
(PS: I know I can use link/cut trees for this, but I'm explicitly asking about Euler tour trees. Not really for a problem (though you could test on e.g. SPOJ's DYNACON1), I'm just curious if this is possible (the fact that this rerooting is described in various lecture slides suggests to me that it is))











Try storing directed edges in Euler tour instead of vertexes. E.g. instead of
1 2 4 2 5 2 1 3 1you would store(1, 2); (2, 4); (4, 2); (2, 5); (5, 2); (2, 1); (1, 3); (3, 1)(any self-balanced tree would do, e.g. Cartesian/Treap or Splay). The nice thing of such representation is that invariants are very simple:Modifications:
The only problem is with isolated nodes, but that can probably be solved by adding an imaginary edge from vertex to itself, which is never removed.
Anyway, all operations look like .
.
Thanks for your answer!
I'll point out that I was actually trying to combine rerooting with a
cut(u)operation (i.e. 'cut u from its parent') rather than acut(u, v)operation, but I guess the former doesn't really make a lot of sense when combined with rerooting. (parents constantly changing and all that) I think it's just not possible at all.Adding self loops to vertices is also a nice idea, in fact I think it makes the 'add an edge (u, v)' operation much easier. After all, you say 'find an arbitrary edge ending in u'. You could manually keep a pointer to such an edge, but then you'd have to find a new one everytime such an edge is deleted. But when there are edges (u, u) in the tree you could always pick that edge to insert the new subtree after.
Oh and self-loops also allow us to keep aggregate information for both edges and vertices in a subtree :-)
How can we answer subtree queries using this representation?
In the one mentioned in the blog we keep track of first & last occurrence of a node in the Euler Tour which makes finding the subtree of a particular node very convenient.
Here I think we should instead keep track of the first edge where a node appears and the last edge where it appears also. But this way we're back with the same problem mentioned earlier.
I think I'm missing something and any help would be greatly appreciated!
If you know parent of a vertex, you can cut the corresponding edge, query the whole tree, and then link the edge back.
However, knowing the immediate parent (as opposed to known just the root) for each vertex is probably hard with pure Euler tour trees. I don't remember any good tricks for that right away.