I couldn't find a place to discuss this.
When will we get results? Is anyone confident with B or F?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
| Name |
|---|



I was wondering the same :).
I think my idea of B is right, but there could always be an implementation bug (especially since the sample cases were very small; I did not stress test my solution). What I did was for each subtree compute how much beacon time from the root you need and how much beacon time you have remaining if you need to traverse this entire subtree. And then do another dfs to determine final node you are going to end up in. The have/need for the parent structure is passed as a parameter to this function and have/need for the siblings can be calculated with prefixes and suffixes from the first calculation.
Hm, I have the same feeling about B (idea seems right, but could have bugs), but my solution does not have any prefixes and suffixes :)
Basically, for each vertex we compute the number of vertices a and the total power p in its subtree (we root the tree at 1). If p<a, then there's no solution. Now we look at complements: n-a and total_power-p. Let delta be n-a-(total_power-p). If delta>0, it means that the path from 1 to the final vertex must go at least delta steps towards our vertex. Now we have constraints like "the path to final vertex must go at least x steps towards vertex y", so with another dfs we can find all edges that must lie on the path to final vertex, and then we just check if they lie on one path, if yes, extend it down as much as possible, and finally check that total_power is enough for that traversal.
And that's exactly what happened: had a really tiny bug, more specifically that in the "if p < a, there's no solution" line above we should exclude the subtree corresponding to the root (full tree), since the root does not need to be entered. A one-line fix, and it passes in upsolving :)
Would've been really amazing to win after not being able to solve any problem for the first hour.
I had exactly the same bug! In addition, I also had an overflow, but with those two fixes my solution passes in upsolving.
Would not have meant a win for me (Gennady was just too fast for that), but for me a second place also counts as 'amazing' :).
Were you really not able to solve E for first hour :P?
"solve"
Solving E in one hour is pretty tough. Good thing all of us already "solved" the exact same problem about a dozen times already.
Seriously, what kind of problem-setting is this? "I made 5 problems and don't feel like making another one, just throw in Catalan numbers or something"
Well, I find the problem nice enough for the easiest problem. I've spent a couple of minutes thinking before I got the Catalan numbers idea. It seems I'm not the only one who haven't got the idea instantly, so the problem is ok.
I definitely agree, I read this problem and was like "wtf, did they just give me Catalan's number definition?" and spent more time convincing myself that there is no hidden trap here and it really is just Catalan than actually solving this problem :P. Especially after participating in dozen of Andrew Stankevich contests there shouldn't be anyone out there who doesn't know what Catalan numbers are xd. I don't know which definitions people that needed to think about it know (because Catalan's numbers have a lot), but what is described in statement is in my opinion best known one (maybe after slight change that Um_nik mentioned), so I see no point of posing that problem in a contest. At least I got a screen when I was leading, but that would be it for my today's achievements xD.
Yes. Well, I've been trying to solve D and E, since everybody was submitting them. I've briefly switched to F, implemented incorrect approach, and submitted it, but that took me probably 15 minutes or so. So the remaining ~1 hour before my first accepted run I spent on D and E, I think roughly equal — about half an hour for each. Since coding for E is trivial, all this half an hour was spent before noticing that those are Catalan numbers.
I guess I did not implement the slow solution and notice the pattern because of the logic that W4yneb0t alludes to: this is Yandex.Algorithm finals, they won't give a sequence that is OEISable :)
Ehm... Isn't it like the definition of Catalan numbers? Just assume that each player can take only one stone in one move but they don't have to alternate moves.
Yes, rub it in :)
I don't know what else to say. Yes, in hindsight it's obvious. But I still spent 30 minutes before seeing it.
Approximately in 2 hours from now there will be an award ceremony, after that the results will be unfrozen.
Btw, since there are also a number of people competing onsite, I think they will be announcing the results in some kind of award ceremony, which might take a while.
I also asked a question (using the messages) about when the results will become available a while a go, but haven't received an answer yet. I am afraid that whoever is answering the messages is now also busy with the award ceremony.
Formulas for calculating bonus penalty work awful at contests like this. I think getting -13, -6 or -0 (lol) minutes for blind submit is a joke. Maybe you should set a lower bound -20 or -40 minutes next time?
The choice between submitting open and blind shouldn't be obvious. Since almost everyone solved those 3 problems, you should be almost certain that your solution is correct, so you will have some incentive to submit blind even if the bonus is very low. Predicting whether a task will have -0 or -20 for a blind submission could also be considered a skill.
Is there a way for non-contestants to see (and try) the problems?
Yea, guys, how to see problems?
Maybe you can try here: https://contest.yandex.com/algorithm2017/contest/4737/enter/
So, does anyone have any ideas on how to solve F? Even solutions that timed out, but are still runing in reasonable time will be welcomed.
What is reasonable time for you? I think that obvious O(6n) can be sqeezed through TL with some hacks.
If the dimension of linear space is big (close to n) then for each number there are few corresponding subsets and for many branches it is obvious that Bob wins because he forbade all good subsets.
If the dimension is small then: are essentially the same. If two numbers are the same then Alice only need one of them and she can guarantee that she will get one (after Bob take one, Alice take another). When the dimension is small we can significantly (or not) reduce search space.
are essentially the same. If two numbers are the same then Alice only need one of them and she can guarantee that she will get one (after Bob take one, Alice take another). When the dimension is small we can significantly (or not) reduce search space.
1. The amount of numbers to check is not so big
2. If Alice already has some set of numbers X then a and
Also I have a hypothesis that in every state Alice can win for numbers in some linear space. If it is true then we can solve the problem in O(3npolynom(n)).
For a faster solution, after making this observation, the problem becomes much easier:
Let span(X) denote the set of xors of a subset of X.
Suppose Alice currently has set A, and she wants to get k. Alice can win if and only if there exists two disjoint subsets B1 and B2 such that span(A+B1) = span(A+B2) and k is in span(A+B1).
We can use this fact with A = {} to get a simple winning condition for Alice.
After making that observation, there is a straightforward O(3n * n) solution. It's possible to speed up to O(2n * poly(n)), but I didn't think it was easy to squeeze a O(6n) solution, so that's why the bounds are so low.
Can you prove the "only if" part of that observation? It sounds like some theorem about augmenting paths in matroids, but I can't get it to work.
Maybe I should also ask why no editorial has been posted...
Yeah, I have a proof (it's a bit long). Basically, the idea is to use induction.
Anyways, I think there are written editorials somewhere that were given to finalists, but I'm not sure why they haven't been published.
The first direction is there exists two disjoint subsets B1, B2 such that span(A + B1) = span(A + B2) and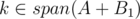 => Alice wins.
=> Alice wins.
Let's prove this by induction on rank(A + B1) - rank(A). This is true for 0, k is already in the span of A. In addition, this is true for a rank 1, since if there are two different positions x, y such that A + {ax} and A + {ay} have the same span that include k, Alice can just choose whatever element that Bob doesn't choose.
For the inductive step, suppose we have two disjoint subsets B1, B2. If Bob doesn't take away anything from B1 or B2, Alice can just do anything on her move. Otherwise, suppose Bob takes away the number p from B1. Furthermore, let's assume that p is not in the span of A, so in particular rank(A + {p}) > rank(A). There is an element q in B2 such that span(A + B2 - {q} + {p}) = span(A + B2) (by a basis exchange argument). So, we can induct on B1 - q, B2 - p.
We'll show that if Alice currently has the subset A and has a winning strategy, then there exist disjoint subsets B1, B2 such that span(A + B1) = span(A + B2) and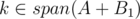 .
.
Let's define a "round" to be one of Bob's turn and one of Alice's turn. We will induct on the number of rounds that Alice needs to guarantee a win (i.e. her current subset's span includes k). This is similar to inducting on rank(A + B1) - rank(A), but we don't know what B1 is.
First, let's assume that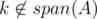 (otherwise, Alice has already won). If Alice can win in one round, the only possibility is that there exists two distinct positions x, y such that A + {ax} and A + {ay} such that
(otherwise, Alice has already won). If Alice can win in one round, the only possibility is that there exists two distinct positions x, y such that A + {ax} and A + {ay} such that 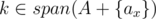 and
and 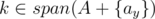 . Since the span of A doesn't include k, we can verify that span(A + {k}) = span(A + {ax}) = span(A + {ay}), so this proves the base case.
. Since the span of A doesn't include k, we can verify that span(A + {k}) = span(A + {ax}) = span(A + {ay}), so this proves the base case.
For the inductive step, let's suppose Bob removes some arbitrary number on his first turn and Alice can win by taking q. By induction, there are two disjoint subsets X1 and X2 such that span(A + X1 + {q}) = span(A + X2 + {q}) and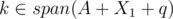 . In addition, we may assume that
. In addition, we may assume that 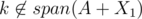 (since otherwise, we would already that X1, X2 is a pair of good disjoint subsets).
(since otherwise, we would already that X1, X2 is a pair of good disjoint subsets).
Now, let's assume Bob instead chose q, and Alice can respond by by taking r and win. Then, there must be two disjoint subsets Y1 and Y2 such that span(A + Y1 + {r}) = span(A + Y2 + {r}) and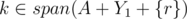 (and again, we can assume
(and again, we can assume 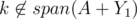 ).
).
We know that q is not in any of the sets X1, X2, Y1, Y2.
Now, let's consider Z1 = Y2 + X2 + {r}, and Z2 = Y1 + X1 + {r}.
We can verify that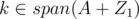 and
and 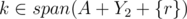 and
and 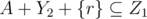 . In addition, we can check span(A + Z1) = span(A + Y2 + X2 + {r}) = span(A + Y2 + X2 + {k}) = span(A + Y1 + X1 + {k}) = span(A + Z2).
. In addition, we can check span(A + Z1) = span(A + Y2 + X2 + {r}) = span(A + Y2 + X2 + {k}) = span(A + Y1 + X1 + {k}) = span(A + Z2).
Let Z1' = Z1 - Y1 and Z2' = Z2 - Y2. Now note that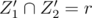 . In addition, we can check that rank(A + Z1') = rank(A + Z1) since any
. In addition, we can check that rank(A + Z1') = rank(A + Z1) since any 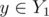 is in span(A + Y2 + {r}), so, in particular span(A + Z1') = span(A + Z2').
is in span(A + Y2 + {r}), so, in particular span(A + Z1') = span(A + Z2').
We can check that the two sets Z1' + {q} - {r} and Z2' are a pair of good disjoint subsets. To verify this, we can check that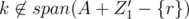 , while
, while 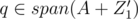
Apologies if I'm missing obvious things here, but I need clarifications:
Why is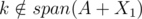 ? Couldn't it be the case that instead, span(A + X1) ≠ span(A + X2), which would also prevent X1, X2 from being a good pair?
? Couldn't it be the case that instead, span(A + X1) ≠ span(A + X2), which would also prevent X1, X2 from being a good pair?
Why is span(A + Y2 + X2 + {r}) = span(A + Y2 + X2 + {k}? I see why k is in the left set, but why is r in the right set?
Why is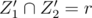 ? Can't something be in both X1 and Y2?
? Can't something be in both X1 and Y2?
Still not clear. I replied in http://mirror.codeforces.com/blog/entry/53354?#comment-384145 so Codeforces doesn't squish the comments.
How to prove the solution of problem C? I know the solution is sort xi and add points start from largest xi. But I cannot prove it.
Let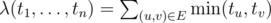 . Say, the input weights are sorted non-increasingly (x1 ≥ x2 ≥ ... ≥ xn). We want to show the existence of
. Say, the input weights are sorted non-increasingly (x1 ≥ x2 ≥ ... ≥ xn). We want to show the existence of 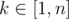 such that λ(y1, ..., yn) ≥ λ(x1, ..., xn) for
such that λ(y1, ..., yn) ≥ λ(x1, ..., xn) for 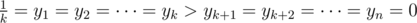 . Then, λ(y1, ..., yn) is equal to the density of the subgraph containing k heaviest vertices.
. Then, λ(y1, ..., yn) is equal to the density of the subgraph containing k heaviest vertices.
We'll take the input sequence of weights (x1, ..., xn) and transform it into (y1, ..., yn). If already some k largest elements of (xi) is equal to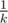 , we're done. In the opposite case, take two largest weights x1, xa + 1 and say that x1 = x2 = ... = xa > xa + 1 = xa + 2 = ... = xa + b > xa + b + 1 (assume xn + 1 = 0).
, we're done. In the opposite case, take two largest weights x1, xa + 1 and say that x1 = x2 = ... = xa > xa + 1 = xa + 2 = ... = xa + b > xa + b + 1 (assume xn + 1 = 0).
Now, we want to transform (x1, ..., xn) into (x1', ..., xa + b', xa + b + 1, ..., xn) so that x1' = x2' = ... = xa' ≥ xa + 1' = xa + 2' = ... = xa + b' ≥ xa + b + 1, the sum of weights is equal to 1, at least one of the inequalities is an equality, and λ((xi')) ≥ λ((xi)). Now, the choice of x1' determines uniquely the new sequence of weights. Moreover, it's not hard to see that λ is a linear function on x1'. It means it suffices either to minimize x1' (in this case xa' becomes equal to xa + 1') or to maximize x1' (in this case xa + b' becomes equal to xa + b + 1).
A single step increased the value of λ and reduced the number of distinct non-zero weights in the sequence. We apply this step until a single such non-zero weight is left and in this way we arrive at the sought sequence (y1, ..., yn).
Thank you! I got the idea!
Somewhat more elementary proof. For simplicity consider the case n = 4. Suppose that x1 ≥ x2 ≥ x3 ≥ x4, and λ = ax2 + bx3 + cx4.
When x1 ≥ x2 ≥ x3 ≥ x4 and x1 + x2 + x3 + x4 = 1, it is natural to replace them with non-negative p, q, r, s such that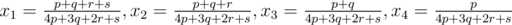 . Then,
. Then,
This is a weighted harmonic mean of {(a + b + c) / 4, (a + b) / 3, a / 2, 0}. We can find subgraphs with density {(a + b + c) / 4, (a + b) / 3, a / 2, 0} as you described.
Here is a proof which seems most natural. We would like to find a subset A such that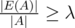 , or equivalently |E(A)| ≥ λ |A|. Let Ap = {xi|xi ≥ p}. Then
, or equivalently |E(A)| ≥ λ |A|. Let Ap = {xi|xi ≥ p}. Then 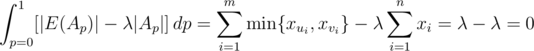 .
.
Therefore we can find some p for which this quantity is nonnegative. (When Ap is empty, it contributes 0 to the sum so we can find some nonempty set.)
WOW only red coders commented here. Let me be one of them.
(Continued from http://mirror.codeforces.com/blog/entry/53354?#comment-383895)
But can't the progress come from the fact that span(A + X1) ≠ span(A + X2) but span(A + X1 + {q}) = span(A + X2 + {q})? That still means that she can't simply skip q. When you say "since otherwise, we would already that X1, X2 is a pair of good disjoint subsets", you are saying "if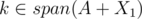 and
and 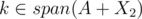 then we proved what we needed to prove". But you actually didn't, you needed to prove there are two disjoint sets where spans contain k and the spans are equal, but what you actually proved is there are two disjoint sets where spans contain k. You proved something weaker than your induction hypothesis, so induction doesn't work.
then we proved what we needed to prove". But you actually didn't, you needed to prove there are two disjoint sets where spans contain k and the spans are equal, but what you actually proved is there are two disjoint sets where spans contain k. You proved something weaker than your induction hypothesis, so induction doesn't work.
Yes I think you're right that the sentence is not correct (i.e. "In addition, we may assume..."). I think this relates to your third point, why does r lie in the span of the right hand set? So, I think it should instead be that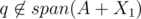 (since this means Alice makes no progress by choosing q). You can use this to show that span(A + X1 + {q}) = span(A + X1 + {k}), and similarly span(A + Y1 + {r}) = span(A + Y1 + {k}).
(since this means Alice makes no progress by choosing q). You can use this to show that span(A + X1 + {q}) = span(A + X1 + {k}), and similarly span(A + Y1 + {r}) = span(A + Y1 + {k}).
If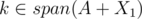 and
and 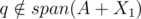 , I don't think span(A + X1 + {q}) = span(A + X1 + {k}) can hold.
, I don't think span(A + X1 + {q}) = span(A + X1 + {k}) can hold.
I'm not trying to be a dick and point out typos, I just don't have any intuitive understanding of the proof idea starting at the 4th paragraph, so I have no idea what you are trying to say...
No worries. About intuition, we are just showing that a pair of good subsets exist using induction and the fact that Alice can win, which are two really strong assumptions. The basic proof idea is adding together these sets that I can magically get from these two assumptions to get a good pair of subsets, but the details are kind of complicated as you can see.
For your point in particular, I think we do need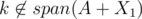 . To show this, I think we can show if
. To show this, I think we can show if 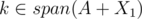 and
and 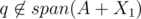 , we can find two subsets
, we can find two subsets 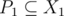 and
and 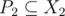 that are a good pair of subsets, or Alice can find another q' with X1', X2', such that
that are a good pair of subsets, or Alice can find another q' with X1', X2', such that 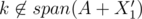 and
and 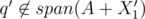 .
.
More specifically, we want elements of P1 to be the ones necessary to form k. In addition, we want elements of P2 to be the ones necessary to form P1 and vice versa (this is mutually recursive). If we relax it to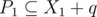 and
and 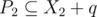 , then since they have the same span, we are guaranteed that all steps are valid, and this process will terminate. The psuedocode might look something as follows:
, then since they have the same span, we are guaranteed that all steps are valid, and this process will terminate. The psuedocode might look something as follows:
So there are two cases, q is never included in P1 or P2, or q is added at some point to one of the sets. For the first case leads to the P1, P2 being a good pair of subsets, and the second case lets us do induction on the number of steps needed to include q in one of the subsets (in particular, we have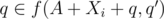 for some i and q', and we can induct with q').
for some i and q', and we can induct with q').