Xsquare's blog

Invitation to CodeChef July Cook-Off 2017!
By Xsquare, history, 7 years ago, In English

Hello CodeForces Community!

I would like to invite you all for the July Cook-Off 2017 (https://www.codechef.com/COOK84)! Five challenging problems will be waiting for you to be cracked during the contest.

Joining me on the problem setting panel are:

  • Problem Setter: Xsquare (Prateek Gupta) and Sundar (Sundar Annamalai)
  • Problem Tester: PraveenDhinwa (Praveen Dhinwa) and arjunarul (Arjun Arul)
  • Editorialist: Xsquare (Prateek Gupta)
  • Russian Translator: CherryTree (Sergey Kulik)
  • Mandarin Translator: huzecong (Hu Zecong)
  • Vietnamese Translator: VNOI Team
  • Contest Admin: Kamil Debowski (Errichto)

I hope you will enjoy solving them. Please give your feedback on the problem set in the comments below after the contest.

Now, without further ado, let me share the contest details with you real quick:

Time: 23rd July 2017 (2130 hrs) to 24th July 2017 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.

Details: https://www.codechef.com/COOK84

Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.

Prizes: * Top 10 performers in Global and Indian category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. Know more here: https://www.codechef.com/laddu. (For those who have not yet got their previous winning, please send an email to winners@codechef.com)

  • Vote: I like it
  • +22
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +17 Vote: I do not like it

Please, proofread the statements before contests. It's sometimes really hard to decipher what did an author mean. After reading the Bipartite Graph from Trees statement several times I have no clue what the problem is.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please add problems to practise section.

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

How to solve the last problem? (I mean Chang and Beautiful Sequences)

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 7   Vote: I like it +8 Vote: I do not like it

    Consider how many times the i-th bit (where 0 ≤ i < 20) shows up in all of the bitwise XOR's. You should see a pattern!

    For example, consider N = 2 with the sequence consisting of 3 = 0112 and 4 = 1002.

    The last bit shows up three times:

    2 + 1 + 0 = 3

    Similarly, the 2nd-to-last and first bit show up three times as well.

    So the total beauty is

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      So we get two formulas.

      If there is only one bit that row then it is (n+1)*(2^(n-2)) * (2^k).

      If more than one bit then it is n*(2^(n-2)) * 2^k.

      If zero its zero

      So now do u run on all bitmasks assuming if 1 it is only one bit active and else zero or many other. Complexity around 20*(2^20).

      Is this intended solution??

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 4   Vote: I like it +25 Vote: I do not like it

    If you have a sequence of k ones and n - k zeroes, the sum of lengths of sequences with xor = 1 is given by the derivative of:

    at x = 1

    It breaks into three cases :

    • . The number of such sequences is a = 1.
    • . The number of such sequences is b = n.
    • . The number of such sequences is c = 2n - n - 1.

    Now, we have these sequences for all bit positions. Say the mask of positions with k = 0 is m0, and mask of positions with k = 1 is m1, and mask of positions with k ≥ 2 is m2, then:

    n2n - 2(M - m0) + m12n - 2 = b

    We can iterate over all submasks m0 of M, and use modular inverse to find m1. Accept this pair (m0, m1) if and only if m0&m1 = 0 and m0|m1 is a submask of M. m2 = M - m0 - m1. If x0, x1, x2 is the number of set bits in m0, m1, m2 respectively, then we add ax0bx1cx2 to the answer.

    Solution Link

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve D ?

→ Reply
»
7 years ago, # |
  Vote: I like it +2 Vote: I do not like it

Is the intended solution for BIPARTE just finding the max flow using hopcroft karp algorithm? I got TLE doing the same but many others got AC.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Expected solution is to convert it to a flow network with O(M+N) vertices and O(M+N) edges and compute flow in it. Some Hopcroft Karp and brute force matching(which should have given TLE) ran much faster than expected,

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      What is the fastest way to solve it?

      If we use Dinic for max flow then the complexity O(V2E), while brute force matching is O(VE) and Hopcraft Karp is O(V0.5E), Then why are Flow solutions faster than the Matching solutions.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        The network we define in flow solution has only O(V) edges but the matching solution can have O(V^2) edges. So comparing the expressions of complexity isn't correct as E is different.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        As far as I know . The bound for dinic O(V*V*E) is a general one and I have read it can be be proved that bound is O(√V *E) for bipartite matching using Dinic. So knowing Hopkropt for a bipartite matching is not of much use complexity wise

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Time Complexity of Dinic for Unit Capacity Networks is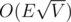

        → Reply
»
7 years ago, # |
  Vote: I like it +37 Vote: I do not like it

So, apparently there was another hoax in this contest as well.

I was scanning through submissions of a person and saw his couple of O(n^2) solution getting passed. Seems like it has been evaluated in IOI style or something but on the scoreboard 1 full mark is given in ICPC style! Interesting right? :P

Submission Links
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    This happened to me and I just ignored it, but my solution was wrong! So much for solving all problems D:

    Link

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes they messed up scoring for that problem.

    → Reply