GreenGrape's blog

Codeforces Round #426 Editorial
By GreenGrape, 7 years ago, translation, In English

We, the round authors, are eternally grateful to all the brave who took part in this round. Sadly there were some issues to encounter, but we hope it only made the contest more interesting :)

Tutorial is loading...

Code: 29027824

Tutorial is loading...

Code: 29027867

Tutorial is loading...

Code: 29027782

Tutorial is loading...

Code (divide & conquer, GreenGrape) 29027705

Code (divide & conquer, xen) 29027883

Code (lazy propagation) 29027667

Tutorial is loading...

Code: 29027757

Tutorial is loading...
Code: 29027729
Tutorial is loading...

Code: 29027876

  • Vote: I like it
  • +45
  • Vote: I do not like it

Comments Comments (55)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

https://translate.yandex.com/

→ Reply
»
7 years ago, # |
  Vote: I like it +30 Vote: I do not like it

I think it is important to mention in this analysis that Div2 C gives TLE without using some IO optimizations such as ios::sync_with_stdio(0), cin.tie(0) and '\n' instead of endl, or using scanf/printf. Maybe some other languages have the same problem with IO. So, even if you have right solution with O(log(ab)), it is quite possible to get TLE.

I tested my code with different combinations of IO optimization and only combination of all the mentioned methods (without using scanf/printf) gives AC.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Yes!

    For some reason I forgot that there would be alot of input-output data in the problem and thats why i am getting TLE on pre-test 8...kept on thinking about a better way to finding cube-root for sometime when it struck me right before the end of the competition that i have to use scanf/printf...

    Wasted about an hour on that :(

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      You can use binary search to find the cube root. The complexity is only O(nlog(xy)) Let the left pointer be 1 and the right pointer be 1000000, and it will not get TLE.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        My solution doing exactly the same. l = 1 and r = 1000010. Binsearch. TLE 8.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          cin is much slower than scanf. You can use scanf instead of cin, or just like you previously said, using some IO optimizations. You can see my submission as an example.

          → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        You will be surprised:)

        I have three solutions. One with binary search, one with newton method and one with function from math.h package and if you use cin/cout your solution will fail on test 8.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          If you use the function from math.h, you will have to check for (cbrt(a*b)+1) and (cbrt(a*b)-1) also correct? or maybe just one of them? 'cause it will give precision error...

          → Reply
»
7 years ago, # |
← Rev. 4   Vote: I like it +1 Vote: I do not like it

Nice solution in div2 C :)

I had an idea that we could imagine S and P as composition of prime numbers. For example: a = b = 8 = 23, each game add 21 to S/P and 22 to another set. As we see, game could be only if summary power of 2 in P and S divided by 3 (2 + 1 = 3) and.. some another checks. But it will not pass anyway, cntprime is too big for sqrt(109).

P.S. cubic root could be found in O(1)? Or you mean single function call..

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    No, you cannot find cuberoot in O(1)... it'll take about O(log(n)) to find the cuberoot of n using binary search...O(1) is for EACH query...

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    There is the function cbrt, but I don't know how it is computed.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yes, that is what about I asked )

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      cbrt() gives precision error for large values...it is preferred to use binary search to find the cuberoot...

      cbrt() function also takes O(log n) time as far as i know.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        If cbrt() function takes O(1) (not sure) then precision problem can be solved to make it efficient we store cbrt() in an int say x and then check whether x*x*x is our number or not if it is then x is perfect cube root otherwise not.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          As i said before, cbrt function doesn't take O(1) time, it takes O(log n) atleast...otherwise i wouldn't have gotten TLE for this solution...

          → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +6 Vote: I do not like it

    Or you can use unordered_set, and insert all n^3 values for n = 1..10^6 before input. So you can check whether number is cube for O(1) in average.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +6 Vote: I do not like it

The time limits of problem C seems to be very strict.

Fast IO — Time limit exceeded

Scanf/printf — passed.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This is always the case when there's at least a couple megabytes of input. Just use cstdio with such problems.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have to ask one more thing. I thought of one more approach for problem C although I believe it might exceed time limit but the problem is that I am getting wrong answer. Just wanted to know the reason behind it.

My idea is to take input two given numbers and factorise them.

Then start subtracting/erasing smallest prime number in both of them according to need.

For example if a is having 2 in its prime factors with power 1 and b is having 2 with power 2 so subtract one and two accordingly. When power of a number becomes 0 , erase that.

If at any point of time till all factors get erased from map/vector, the lowest prime factors of both numbers are not equal, print No.

If everything passes successfully, print Yes.

Do I have missed anything in my solution?

My solution — http://mirror.codeforces.com/contest/834/submission/29031585

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can anybody help out please?

    I have already mentioned all details related to my problem.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      This approach in order n*sqrt(n). But to pass all the test cases we need order n*log(n).....As mentioned in the editorial.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I know the problem with time limits. I am asking about if there is any problem with my approach because I am getting a wrong answer.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          1
          800018 4

          Your code gives 'Yes'.

          There is problem with 'fac' method: if there any prime > N > sqrt(X) — you won't know about it.
          At this testcase your program solves test '2 4', not '2 * 400009, 4'.

          → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think when we decide whether two powers m, n are valid we can check this:

    Suppose A wins x times, B wins y times, then we have 

    2*x + y = a;
2*y + x = b;

    then 

    x + y = (a + b) / 3;
x = a - (a + b) / 3;
y = b - (a + b) / 3;

    So we need to check whether 

    1. (a + b) % 3 == 0
2. a - (a + b) / 3 >= 0
3. b - (a + b) / 3 >= 0
    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oh your approach seems so cool.

      Purely mathematical.

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      (a+b)%3 == 0 for every power implies that their product must be a perfect cube, and since the power of every prime in the cube root will be (a+b)/3, a — (a + b) / 3 >= 0 and b — (a + b) / 3 >= 0 will only hold if the two numbers are divisible by the cube root. Your method is exactly same as the one mentioned in the editorial :)

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you find out what's a time complexity with my code? ( Div2 C) 29033678

I think it's O(sqrt(a)+sqrt(b)).But I got TLE in test8

thank you

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It's actually O(n * (sqrt(a) + sqrt(b)), which takes about 1010 steps in total.

    → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Content of Bakery is full of mistake.

→ Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

In case someone is scared away by the treap in 1D's model solution: replace it with a binary indexed tree of size 4n and things will be fine (and faster!).

→ Reply
»
7 years ago, # |
  Vote: I like it +41 Vote: I do not like it

About Div1-B: we can write D&C solution with O(NKlogN) complexity.

We need build persistent segment tree for queries 'amount of unique numbers on [l; r]'.
And we need array next[i] — such index that a[i] = a[next[i]], i < next[i].

Now in D&C calculation we have M — index on current layer and [start;end] — limits of previous layer.
We can do exactly one query to PST about segment [end + 1;M] in O(logN).
After that we iterate prevIndex from end to start and update amount of unique numbers in O(1) — it increases only if next[prevIndex] > M.

So, additionaly to standard D&C we do one query in O(logN) for each index on current layer, total complexity is O(NKlogN + NKlogN) = O(NKlogN).

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    Can you please sketch a proof how opt(i,k) <= opt(i+1,k).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      So what we need to proof? That opt(i, k) ≤ opt(i + 1, k).
      Let's use proof by contradiction. X = opt(i, k), Y = opt(i + 1, k).
      And we assume that !(X ≤ Y) = (Y < X).

      When we did search for dp[i][k], we choosed X, not Y.
      It means, that dp[y][k - 1] + unique(y + 1, i) ≤ dp[x][k - 1] + unique(x + 1, i).
      So unique(y + 1, i) - unique(x + 1, i) ≤ dp[x][k - 1] - dp[y][k - 1].

      But by our assumption dp[y][k - 1] + unique(y + 1, i + 1) > dp[x][k - 1] + unique(x + 1, i + 1).
      So unique(y + 1, i + 1) - unique(x + 1, i + 1) > dp[x][k - 1] - dp[y][k - 1].
      It's obvious that unique(y + 1, i) ≤ unique(y + 1, i + 1) ≤ unique(y + 1, i) + 1. The same about unique(x + 1, i).

      1. unique(y + 1, i) - unique(x + 1, i) ≤ dp[x][k - 1] - dp[y][k - 1].
      2. dp[x][k - 1] - dp[y][k - 1] < unique(y + 1, i + 1) - unique(x + 1, i + 1).
      3. unique(y + 1, i) ≤ unique(y + 1, i + 1) ≤ unique(y + 1, i) + 1.
      4. unique(x + 1, i) ≤ unique(x + 1, i + 1) ≤ unique(x + 1, i) + 1.

      From 1 and 2 we have

      • unique(y + 1, i) - unique(x + 1, i) < unique(y + 1, i + 1) - unique(x + 1, i + 1).
      • unique(x + 1, i + 1) - unique(x + 1, i) < unique(y + 1, i + 1) - unique(y + 1, i).

      Last inequality could be possible only if unique(x + 1, i + 1) = unique(x + 1, i) and unique(y + 1, i + 1) = unique(y + 1, i) + 1.
      But it means that a[i + 1] isn't unique on segment (x + 1, i + 1), but unique on segment (y + 1, i + 1).
      It can't be true, because y < x, so if segment (x + 1, i + 1) contains duplicate of a[i + 1] — segment (y + 1, i + 1) contains it too.
      So we went to contradiction, that proofs X = opt(i, k) ≤ Y = opt(i + 1, k).

      Sorry for so long proof, I'm not very good at theoretical part of Divide&Conquer dp trick, so maybe there exists more elegant and shorter proof.

      → Reply
      • »
        »
        »
        »
        4 months ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Sorry but i do not understand most about Dp Dnc :(. I have a question that if we can proof that opt(i,k)<=opt(i+1,k), so why we can not choose the last one since opt(i+1,k)<=opt(i+2,k) ... until i=k-1. I know it's wrong but i can not prove it ... ?

        → Reply
        • »
          »
          »
          »
          »
          4 months ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          ah, i understand that, opt(i,k) means that the most optimize point that we will choose if we consider dp[i][k], and so do opt(i+1,k). Sorry for my bad :( .

          → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Same approach is giving tle. Can you please help me to solve this? Here is the link to submission.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

834 b can be solved in a single traversal of the string, by maintaining total count of each character.Now, if any character occurs for the first time, then we open the gate and when it's count reduces to zero, then gate is closed. Accordingly keep a gate variable and increment and decrement it in respective situations specified, if at any instant, the value crosses k, print yes otherwise no..

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

dp(k, n) = min1 ≤ i < ndp(k - 1, i - 1) + c(i, n)

should "min" be "max"?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

For problem B in div1, I use divide & conquer optimization and president tree with complexity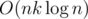 . In a layer we only need O(n) queries in president tree, then other queries can be calculated from these in O(1) time each. See my code for more details: 29023103.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain Div2 D?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem Div2.C why do we need to check that the cubic root divides a and b? Also, although I found integers x and y such that a=x^2 * y and b=x*y^2 my solution still fails. Any ideas why?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If a and b are formed by following the rules of the game then their product will have an integer cube root, however all a and b who's product has an integer cube root may not be formed by following the rules of the game:

    Eg: a = 1, b = 27

    By checking that the cube root divides each number you ensure that it was a factor of each number

    → Reply
»
7 years ago, # |
  Vote: I like it +18 Vote: I do not like it

I'm not sure I understand the described solution to Div1 D, possibly because I'm not very familiar with centroid decompositions. What is a "suffix" of a tree?

My solution is I think O(n log n) operations in Z_M, where some of them are divisions or exponentiation and so take O(log M) time. I haven't checked whether this ends up being O(n log n + n log M) or O(n log n log M) overall.

I use three passes, one to count the total product for all paths, then two more to count it for paths that are too red or too black. For a particular pass I weight the edges as, say -2 for red and 1 for black, and then count only paths with positive total weight. For each subtree I count the number of paths of each possible weight, and the product of their clamminess. So far I think this sounds similar to the official solution, but without the benefit of centroid decomposition to handle balancing. Instead, I use a merging algorithm that can merge trees of size a and b in O(b) time, and always start with the largest child (similar idea to heavy-light decomposition). Each element can thus only be merged O(log n) times.

While this could be achieved with a segment tree, I had a tricky data structure to describe the counts and products on a subtree that had - A deque with an indexing offset, to allow growth at either end, and shifting by a fixed amount (to add the weight of the parent-child edge). - A scale factor that was lazily applied to every path (to account for the clamminess of the new edge). - A combined count+product for all paths with non-negative weight. This allowed computing suffix sums in time proportional to the absolute value of the query weight, and count be adjusted in constant time as the indexing shifted (assuming that all edge weights are O(1)).

This made all the necessary operations on the structure take time scale with the size of the smaller structure being merged in, independently of the size of the merge target.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    For most 'static' counting problem on trees, if it can be solved by so called "centroid decomposition", it can be also solved by a similar technique like yours. As these two solutions take a similar form: "centroid decomposition" deletes a vertex and merge the remaining trees, while yours looks like deleting a path and merging the remaining trees.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain this from the editorial of div1-c : "At a first glance it seems that out bruteforce will end up being O(2^n). But an easy observation shows that there can be no more that two separate branches here. The total bruteforce complexity is O(10·n). "

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Notice that our bruteforce can go two ways only if we got both flags active. But this transition will bring us to two separate cases with only one flag which means we achieved the linear time.

    → Reply
»
7 years ago, # |
  Vote: I like it +31 Vote: I do not like it

div1 C can be solved in .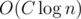

Let's select the first digit in which L and R are different (digits before it can be ignored). [L, R] can be split to , 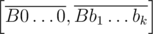and possibly 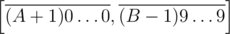if A + 1 < B. Now we can actually make b1 ≤ ... ≤ bk, because if for some index bl > bl + 1 then the sets of inedible tails for segments 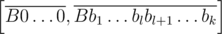and 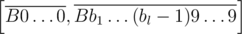would be the same. We can also assume that all inedible tail are filled with zeroes to the same length k + 1.

The key observation is that the set of tails for segment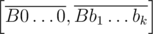 can be split into no more than 10 disjoint sets Β0, ... Β9 each is described as a fixed set of digits and a minimal value for the rest of k + 1 digits (for example the set of tails for [400, 423] is split into {4} and 0, {4, 1} and 1, {4, 2, 2} and 2, {4, 2, 3} and 3). Then we do the same thing for segment and obtain disjoint sets Α0, ... Α9. All we have to do now is calculate the sizes of Αi, Βj and Αi Βj which can simply be done in O(k) given how those sets are described. If A + 1 < B we simply ignore tails that have at least one digit between A + 1 and B - 1 in Αi and Βj while counting and add the number of different tails from 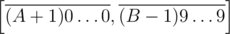to the answer. Total complexity is .

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

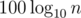submission

getting tle in D. any idea how to optimize it?

couldn't understand the tutorial.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem D (div 2) do we need to pack all n cakes into boxes or just some of them?

→ Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Persistent Segment Trees are unnecessary for div1B, as one can instead use the same trick from 868F, where we have the range "sliding" around. Full disclosure: this trick was obtained from Benq

http://mirror.codeforces.com/contest/833/submission/33818859

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    Can you please elaborate on the trick,cannot understand it completely from your code.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I donot know why are you people down-voting me.Is it wrong to ask something that one cannot understand.Please if anyone can explain the trick.Sorry if it's a very stupid ques.

      → Reply
»
11 months ago, # |
  Vote: I like it 0 Vote: I do not like it

can anybody explain the implementation of solution I working ? $$$dp(k, n) = max1 ≤ i < ndp(k - 1, i - 1) + c(i, n)$$$ I dont think a one-liner can explain it

→ Reply