qoo2p5's blog

Codeforces Round #427 Editorial
By qoo2p5, history, 7 years ago, translation, In English
Problem A. Key races
Problem B. The number on the board
Problem C. Star sky
Problem D. Palindromic characteristics
Problem E. The penguin's game
Problem F. Roads in the Kingdom
  • Vote: I like it
  • +120
  • Vote: I do not like it

Comments Comments (58)
| Write comment?
»
7 years ago, # |
  Vote: I like it -30 Vote: I do not like it

I did a O(nclogX + QlogX) solution for problem C. Where X is the maximum coordinate. Answering each query in O(log X).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

del

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For problem C ,what I am doing is storing the cummlative sum of the value of all stars in a row x upto y at time instant t as cum[x][y][t] for all t<=10 and then for each query I am running a loop for i= x1 to x2 and adding cum[i][y2][t]-cum[i][y1-1][t] to the answer where t=t mod (c+1) .I am getting WA.Can anyone please help? code link : http://mirror.codeforces.com/contest/835/submission/29068753

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Hi! In problem C I tried to do a Brute force solution with some optimization but getting WA for TEST 3. Can someone please look at my code. http://mirror.codeforces.com/contest/835/submission/29078375

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    You must have ignored the possibility of having two or more star at one point.

    See carefully constraint for number of stars (10^5) is more than the grid (100*100)

    → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Does this mean that the right half of abba is actually ab not ba? I was solving it as if the right half was ba.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    It is ba.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I had a huge thing misunderstood during the contest, thanks for clarifying.

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      So the condition was supposed to be "the left half is the reverse of the right half"? or am I understanding something wrong?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I don't think you're right. In the statement: "Its left half equals to its right half", and this is the tricky part.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        No, it wasn't. But we can prove that it is.

        Let's prove that k-palindrome (k >= 1) is palindrome. k = 1 is by definition. k >= 2: s = t + c + t, where t is (k — 1)-palindrome and c is some character or empty string. s is k-palindrome. So, t is (k — 1) palindrome. And we know that t is palindrome. So, reversed(t) = t. And s = t + c + reversed(t) and it is palindrome.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Yeah the editorials for even other contests should be posted fast like this one! :)

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Sorry for my poor English:) Can anyone explain problem B, forth test, i tried to think on it but my answer is also wrong, help me!!! UPD: I FINNALY UNDERSTOOD MY MISTAKE :D

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hello!For problem C.I looked through questions of contestants and my question is quite similar to those. I just can't understand why i got WA on 3 Test. I took into account case, when stars are in one spot, but it didn't help me. It will great help to me if someone will find bug in my code: http://mirror.codeforces.com/contest/835/submission/29064634

→ Reply
»
7 years ago, # |
← Rev. 12   Vote: I like it 0 Vote: I do not like it

For problem C, what I did was storing the brightness of stars in the array and accumulating the (brightness + t) % (maxBrightness+1) inside a given rectangle. Suppose maximum brightness is 4 and the query is (1,1,1,2,2).
The brightness of stars are stored in a following manner:
0 0 0 0
0 1 2 0
0 0 0 0

I am checking from (1,1) to (2,2) and and it produces: (1+a[1][1]) % 4 + (1+ a[2][1]) % 4 = 3 What seems to be a prolbem?

I would appreciate if someone point out the logical defect on the idea. http://mirror.codeforces.com/contest/835/submission/29073973

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    There can be multiple stars at a point. Also, it seems that you are looping through the rectangle of each view, which might be too many operations to fit in the time limit.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In D we should make m = [(l+r)/2]-1 only if length of substring is odd, otherwise m= [(l+r)/2]; By the way, how to use special symbols? like [ ]?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain what is bad with input/output in my solution of E?29084972

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You need to flush the output every time you print. Some languages back up all printing operations into a buffer until there's enough (because printing takes time, so printing a single large string is faster than many small strings). This makes the grader to not be able to see your output; flushing forces the language to actually print it out to the output no matter whether the buffer is full or not. It's also written in the problem statement.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Nope, it doesnt help (in java println workes like flust). I tried to use flush after every print and only after printlns, nothing helps. I dont get where is mb mistake...

      → Reply
»
7 years ago, # |
  Vote: I like it +34 Vote: I do not like it

Proof that 19 questions is necessary for E:

At the worst case, n = 1000, so there are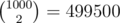 possible answers. You need to find the single correct answer. Each question you ask will give 2 possibilities, so k questions will give 2k possibilities. Of course, you need 2k ≥ 499500, otherwise some answers to the questions will have lump multiple possibilities together. Thus k ≥ 19.

→ Reply
»
7 years ago, # |
  Vote: I like it +17 Vote: I do not like it

For Problem D, I found a simple solution using Palindromic Tree, which runs in O(|s|) time and uses only O(|s|) memory.29085544

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    In fact I found this problem quite similar to another Codechef problem Here, but in this problem the range of |s| is much smaller.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Do you mind explaining your panlindromic tree solution?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It's hard to explain the whole idea of palindromic tree here, this tutorial may be useful.

      First let's define the palindromeness of a palindrome S as the maximum k that S is k-palindrome. In this problem, actually we need to calculate the palindromeness and the number of occurrences for each palindrome.

      The second problem is a basic application of palindromic tree which can be found in the blog above. To deal with the second one, for each palindrome S we need to know the longest palindrome prefix P whose length doesn't exceed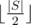 , the palindromeness of S equals to the palindromeness of P + 1 if 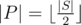. It equals to 1 otherwise.

      So the only remaining problem is to find P for each palindrome. And it's easy to cope with that with similar method of calculating the longest prefix palindrome. You can take a look at my code (where half[S] presents P) for more details.

      Sorry for my poor English, hope you can get what I mean.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I know my code for D is not very efficient, but after testing 5000 'a's in custom test and it runs under 2800ms, I decided to submit it. But it gets TLE on test 30. However I submitted the exact same code after contest it passed. Does anyone knows the reason? Thanks.

Code in contest: 29067565 Code after contest: 29086375

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    You could write to jury. May be technique dependence.

    → Reply
»
7 years ago, # |
  Vote: I like it -12 Vote: I do not like it

Here is a trap in Problem C: There maybe two stars with the same pos! I got WA for many times because of this!

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -10 Vote: I do not like it

I was wondering if problem C could be done using convex hull? Can somebody please explain why not and if yes then how.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Your queries are rectangles so it doesn't make any sense to use convex hull.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Looking For recursive solution For Problem D..

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem D, would anyone like to prove OBS1? i know it's kind of obvious but i still wonder why :L

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I explained it this way: divide our palindrome into 2 halves, while they are identical, i.e. abacaba <- aba <- a. Length of this chain is k, every member in it can be represented as 1-palindrome, so our initial string can be [1..k]-palindrome. (if we assign aba as 1-palindrome, abacaba would be 2-palindrome, if we assign a as 1-palindrome, abacaba would be 3-palindrome)

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    By induction, just assume that for any n <= k, n-palindrome is a 1-palindrome, then prove it for n = k + 1. So, let's take (k + 1)-palindrome, left and right halves of it must be same k-palindromes, which are 1-palindromes by our inductive assumption, thus the whole (k + 1)-palindrome is also 1-palindrome.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      but whole k + 1 palindrome is also 1 palindrome doesn't prove k palindrome is k - 1 straightforwardly,right?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh, sorry, I incorrectly understood OBS1, my bad:)

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Ok then, just change the assumption, now by the assumption for any 1 < n <= k n-palindrome is (n — 1)-palindrome, too. The prove will be the same, the only thing to deal with is the base case for k = 2.

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We can prove by induction on k

    Theorem: if s is k-palindrome, s is also (k — 1) palindrome, k > 1, |s| > 1.

    Case |s| = 1, it's 1-palindrome = palindrome, since there's no definition of a 0-palindrome, there's nothing to prove.

    Base case for induction: k = 2.

    If s is 2-palindrome, s can be written as s' + c + s', s' is 1-palindrome, c is some character, possibly the empty character. Since s' is palindrome, s' + c + s' is also a palindrome, so every string which is 2-palindrome is also a 1-palindrome.

    Induction hypothesis: Every string s which is k-palindrome is also (k — 1) palindrome, |s| > 1, |k| > 2. The hypothesis is recursive until k = 2.

    s is k-palindrome so it can be written as [k — 1] + c + [k — 1], where [x] denotes some string which is x-palindrome.

    Induction step: Let t be a (k + 1)-palindrome string.

    t = [k] + c + [k], c is some character, possibly the empty character (check above the meaning of the [k] notation). Our induction hypothesis says that a string [k] is also (k — 1)-palindrome, so we can replace [k] by [k — 1], so:

    t = [k] + c + [k]

    t = [k — 1] + c + [k — 1]

    A string is k-palindrome if can be written as [k — 1] + c + [k — 1], we just wrote t as this way so t is k-palindrome and the induction is finished.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Problem D,I thought of the solution above. However, I am afraid of the time limit because dp costs O(|s|^2) time and we must compare the string to make sure it's a palindrome, so I think the time is more than O(|s|^2), is this true?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    After understanding the solution c++ code,I understand. Just ignore,please. I can use the result before to decrease much time complexity.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I do not understand the description of problem D clearly.

how is the answer for 2nd sample test case calculated? abacaba => 12 4 1 0 0 0 0

thanks in advance :)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If a string is K-palindromic it will be (K-1)-palindromic as well. That means that for a[1] = 12 we count every possible palindromic string. You can check that there are exist 12 palindromic strings. a[3] = 1 because only abacaba is 3-palindromic string. a[2] = 4, because {aba, aca, aba(2nd time)} are palindromic string but don't forget to add {abacaba} as well because it is 3-palindromic so it is 2-palindromic too. So a simple solution is to find the a[i] table and after do that operation a[i-1] += a[i].

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E

It can be proven that in the given constraints you can't solve this problem in less than 19 questions.

Really interested to know how to prove such a lower bound! :D

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem D, why hashing TLE? I think the complexity of my solution is O(n^2 * log(n)) which is very small (correct me if I'm wrong) .

My submission: http://mirror.codeforces.com/contest/835/submission/29868893

Can anyone help me?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Hashes are slow. The constant factor of your solution is too large.

    The intended solution is O(n2) and you don't need hashing in it.

    → Reply
»
5 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Can anyone please see my code for problem C? I am getting TLE on test 8. This is my code Please help me.

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    your code complexity is n*q which will exceed time limit

    → Reply
»
20 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem F has almost exactly the same model as CF-515-E, and can be easily cheesed using a segment tree.

https://mirror.codeforces.com/contest/835/submission/197225410

(note to self: write explanation later)

→ Reply