misael's blog

How to calculate n^(n-1)^(n-2)...^1 mod M?
By misael, history, 7 years ago, In English

Problem from https://coj.uci.cu/24h/problem.xhtml?pid=3850 exponial(n) = n^(exponial(n-1))

How to calculate exponial(n) mod M?

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

You can use Euler theorem to prove that .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Even then, it is still O(N log M) right?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it +5 Vote: I do not like it

      It should be much lower than that. Here is a code that implements this problem. I've written it just now.

      An idea which might help to prove why it works is that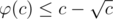 (for a composite c).

      L.E.: According to A007755 it seems that the iterated euler totient function takes O(logC) iterations and an iteration takes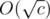 time.

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      We can stop when reach c = 1

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you prove it? For example, a = 2, b = 5, c = 8 is a counterexample.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Well, a and c have to be co-prime. Seems like it's not the case here though.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yes, it is the reason because of I chose that example. However, Can it be used to solve the problem? I mean, exponial(n) and m may not be coprime. I think that you can still solve the problem for each prime factor of m, but I was not sure if it would be optimal.

        → Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

As it says on the online judge, this is from NCPC '16. You can find the solutions here: https://ncpc.idi.ntnu.no/ncpc2016/

→ Reply