A — Bath Temperature
Problem author: teochaban
Editorial author: tomasf
If any tap has the desired temperature, there is no need to open a second tap, so the answer is 1.
Since the resulting temperature is a weighted mean of the opened taps, all obtainable temperatures are between the minimum and maximum temperature available on the taps. If the desired temperature is outside that range, the answer is -1. Otherwise, we can use the minimum and maximum temperature to obtain the desired temperature, so the answer is 2.
Overall Complexity: O(N)
B — Nicoleta's Cleaning
Problem author: tomasf
Editorial author: tomasf
This problem can be solved with a sweep line approach.
First, compress all y coordinates, the resulting coordinates shouldn't be greater than 3·105 since this is the maximum number of distinct y coordinates given in the input. Then sort all points and vertical lines of the rectangles (events) by the x coordinate and process them sequentially. Use a range-update/point-query data structure (like a Fenwick Tree or a Segment Tree) to keep how many rectangles are "active" for every y coordinate. For every vertical line event, indicating the start or the end of a rectangle, update the data structure on the related y coordinate range. For every point event, query the data structure on the related y coordinate and store the answer.
Special care must be taken with indexing since the problem asks for the number of rectangles in which the point is strictly inside. Also, if there are points and vertical lines on the same x coordinate, they must be processed in a specific order so that rectangles that have just started or finished are ignored. The order is: Rectangle end event, point event, rectangle start event.
Overall Complexity: 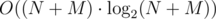
C — Leading the Scoreboard
Problem author: tomasf
Editorial author: tomasf
This problem can be solved by simulating the scoreboard. One of the easiest ways of implementing that is by processing the submissions sequentially while keeping track of what team is leading the scoreboard, how many problems they solved and their total time (penalty). Special care must be taken to handle the occasions in which multiple teams are leading the scoreboard.
Overall Complexity: O(M)
Code(nonsequitur): Link
D — Joaozao, The Digit Maker
Problem author: danft
Editorial author: danft
Let A be the sequence of digits ordered non-decreasingly. Also, let's assume that A is composed of distinct elements. Let 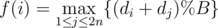 and let G be the functional graph of f.
and let G be the functional graph of f.
There is at least one cycle of size 2 in G.
- If there is a pair (di, dj), such that, di + dj < B. Then it is obvious that if f(i) = k, then f(k) = i, and di + dk < B, as
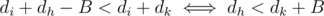 , for any h.
, for any h. - Otherwise, f(2n) = 2n - 1 and f(2n - 1) = 2n (check it)
Solution
- Pick the size-2 cycle with greatest value z = (z1 + z2)%B,
- Add z to the answer
- Remove it from A and rebuild f and G.
- Do this until
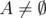
Proof:
First thing to notice is that any other pairing will have value w ≤ z. This implies that the solution we are building is non-increasing. Suppose now that there is an optimal algorithm O that also builds its solution in non-increasing order. Let Ok be the set of available pairings O has available after step k, let also Bk be the set of pairings our algorithm (let's call it B) has after step k.
We are going to prove that max{Ok} = max{Bk}, for any k ≥ 0
Suppose that after step k, max{Ok} = max{Bk}. (base case k = 0 it is obviously true)
if O picks w < z it's not optimal, so it can't be, also by assumption w > z is not possible either.
if O picks w = z it is either the same cycle or a disjoint one (distinct elements assumption), as removing a cycle doesn't do anything to cycles already in G, w will be or has been picked by B and z will be or has been picked by O.
In either case, max{Ok + 1} = max{Bk + 1}.
This is sufficient to prove that our algorithm builds an answer as good as any other algorithm.
Observations:
Without assuming elements are distinct, O could remove a pairing which is not a cycle, the proof would need some small adjustments.
To simplify the implementation, we can remove cycles in any order, as removing one, does not affect others already in G. Also to simplify, let 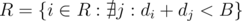 , if f(i) = j and f(j) = i and
, if f(i) = j and f(j) = i and 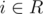 , then
, then 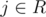 .
.
With both observations, we can implement a simpler solution which starts from i = 2n, and if 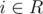 , we skip it, otherwise we add di + df(i) to the answer. After that, we do the same for the elements we had skipped.
, we skip it, otherwise we add di + df(i) to the answer. After that, we do the same for the elements we had skipped.
Overall Complexity: O(nlogn)
E — Double Fence
Problem author: tomasf
Editorial author: tomasf
Let P1 and P2 be respectively the set of points of the first polygon and the set of points of the second polygon. Let ch(X) be the set of points on the convex hull of the set of points X, including colinear points on the edges. A polygon is strictly inside the other if 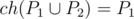 or
or 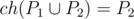 .
.
Overall Complexity: 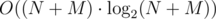
F — No Link, Cut Tree!
Problem author: teochaban
Editorial author: danft
First notice that because the binary tree is a complete binary tree, its height will be 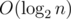 (less than 20).
(less than 20).
Let's denote du as the depth of node u (its distance to the root), and Tu the set of nodes in u's subtree.
Now let's define S[u][d] as the sum of shininess of nodes on depth d, which are in the subtree of u.
In other words, 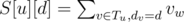
Given a query u, the answer will be the depth d, such that:
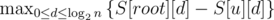
As S[u][d] can be written in funciton of its children:
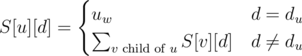
A simple dfs can then be used to compute it.
Overall Complexity: O(Nlog2(N))
G — Hungry Canadian
Problem author: teochaban
Editorial author: danft
Dynamic Programing
The simplest solution for this problem uses dynamic programing on the recurrence:
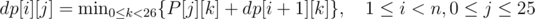
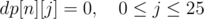
dp[i][j] is the minimum cost of completing the string after having added i characters to it, j being the last one.
The answer will be:
Matrix Exponentiation
Another solution uses matrix exponentiation. Let's define the operator × , which receives two squared matrices A, B and returns a squared matrix C with the same dimension n:
Pk (the matrix of costs to the power of k) = P × P × ... × P, will have the minimum cost to build a string of size k. More specifically Pijk is the minimum cost of building a string of size k starting with character i and ending with character j.
Proof
Let's prove it by induciton on k.
The base case k = 1 is correct by definition.
Now, assuming that Pk is the matrix of minimum costs of building a string of size k
(Pk × P)ij = min1 ≤ k ≤ n{Pikk + Pkj}
Because the string of minimum cost of length k + 1 is a string of minimum cost of length k, plus one character, Pk + 1ij is the minimum cost of building a string of size k + 1 starting at i and ending at j. It can also be proven that × is associative, which allows us to use fast exponentiation algorithm.
Overall Complexity: O(K) or O(log(K))
H — Eating Pie
Problem author: bssanches
Editorial author: bssanches
This is a max flow problem. First, let's create a graph where every type of pie is a node. Then let's consider every pair of vertices u and v. They'll have an bi-directional edge if the pie with type u appears adjacent to the pie with type v in the array P and, the capacity of this edge, will be the sum of Gi in these positions. For example if P = {1, 3, 1, 2} and G = {1, 2, 4} then we will have and edge between 1 and 3 with capacity 3 and between 1 and 2 with capacity 4.
So for every pair of nodes u and v connected by an edge with capacity C, we know that the amount of candies someone is going to earn if they bought both u and v is C.
Now we are going to add two new nodes, one that is going to be the Joaozao (sink) and the other one the Nicoleta (source). We will assume now that every node that Joaozao reaches are going to be brought by him, the same goes for Nicoleta. Assuming this, we need to garantee that Joaozao reaches the nodes he is obliged to buy (the ones that does not appear in Nicoleta's list), the same for Nicoleta. So we will create an edge from Joaozao to every type of pie he is obliged to buy, this edge will have capacity ∞. We will do the same for Nicoleta.
With this graph now, every node has only 3 possible states:
The node cannot be reached by anyone
The node can only be reached by one person
The node can be reached by both Joaozao and Nicoleta.
For the first case, if the node cannot be reached, it means that the node can be brought by anyone and it is in an isolated component (because the edges are bi-directional). In that case anyone can buy the whole component (so the answer is only to sum all the edges in it).
For the second case, there's only one person that can reach the whole component. In that case the person that reaches should buy all the nodes. Which also means to sum all the edges in the answer.
For the third case, the component can be reached by both of them, so we need to separate it in two components. By doing this we will end up with the second case again. Note that by separating them in two components, we will be cutting some edges and they will not be part of our answer. So we want to cut such edges in a way that the sum of their capacities is minimized. This is a standard mincut/maxflow problem.
To sum it up, the answer is the sum of all edges given in the input (in other words, the sum of the array G) minus the maxflow.
Overall Complexity: Depends on the maxflow implementation, for the Dinic's algorithm it is:
O(E·V2)
Note that in the worst case, the complete graph will have around 40 nodes.
I — Matrix Sum
Problem author: bssanches
Editorial author: danft
Fist thing to notice is that the formula given in the problem statement gives us a clue about where to start. To make things a little bit cleaner let's define R, M and S:
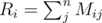
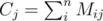
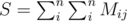
Moving things around a bit we get:
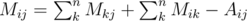
To find Cj, we sum the equation above over i.
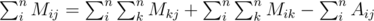


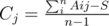
The same thing can be done to find Ri. To get S we sum over the whole matrix M:
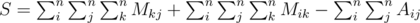
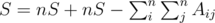
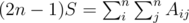
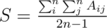
Now we can find Mij using the first equation. Also, when dividing by n - 1 we assumed n > 1, so there's a corner case when n = 1. Also it is obvious that 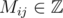 , if and only if
, if and only if 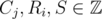 .
.
Overall Complexity: O(n2)
J — Beautiful Triangles
Problem author: bimaoe
Editorial author: tomasf
Let lmin = min(l1, l2) and lmax = max(l1, l2). If the third side of the triangle (l3) is shorter than lmax, the beauty b is given by lmin + l3 - lmax and can be increased by increasing l3. Else, if the l3 is larger than lmax, the beauty b is given by lmin + lmax - l3 and can be increased by decreasing l3. For that reason, the answer is given by l3 = lmax = max(l1, l2).
Overall Complexity: O(1)
K — Counting Good Teams
Problem author: tomasf
Editorial author: tomasf
Let's calculate the number of bad teams (teams that have at least one member that knows everything the other member knows) and subtract from the number of all possible teams. In other words, let's find out the number of distinct pairs i, j in which the bitmask of xi is a submask of xj.
To count the number of bad teams we can use a meet-in-the-middle approach. For every member i, let's split the bitmask xi into xi1 and xi2, the former containing the first 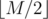 bits of xi and the latter containing the rest.
bits of xi and the latter containing the rest.
Let's define a concatenation operator  that concatenates two bitmasks. For example:
that concatenates two bitmasks. For example: 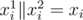 . Let's also define S↑(mask) as the set of all bitmasks x of the same size of mask so that mask is a submask of x. Likewise, let's define S↓(mask) as the set of all bitmasks x of the same size of mask so that x is submask of mask.
. Let's also define S↑(mask) as the set of all bitmasks x of the same size of mask so that mask is a submask of x. Likewise, let's define S↓(mask) as the set of all bitmasks x of the same size of mask so that x is submask of mask.
For pairs of distinct masks xi and xj, the intersection of 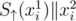 with
with 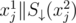 has exactly one element if xi is submask of xj and none otherwise.
has exactly one element if xi is submask of xj and none otherwise.
Let's count the occurrence cntk↑ of each mask 0 ≤ k < 2M when computing 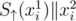 for every mask xi given in the input, and do the same for
for every mask xi given in the input, and do the same for 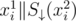 , counting the occurrence cntk↓ of the mask k.
, counting the occurrence cntk↓ of the mask k.
After handling with the pairs that have identical bitmasks, the number of bad teams is given by 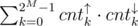 .
.
Overall Complexity: O(2M + N·2M / 2)
Code(tomasf): Link, Link (alternative O(N·2M / 2) meet-in-the-middle solution)










Here is another solution idea for solving problem F No Link, Cut Tree!.
My solution idea for this problem is at first make the given tree a full binary tree. A full binary tree (sometimes proper binary tree or 2-tree) is a tree in which every node other than the leaves has two children. On the other hand A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. So we can convert a complete binary tree to a full binary tree by adding some dummy node whose cost is 0 so that they don’t contribute anything in the solution as well as they will help us to form our solution. Now classify the nodes according to their level and make their cumulative sum or insert them in segment tree or in a binary indexed tree. We need this data structure for every level. Now map the nodes by the inorder traversal of the tree and position of the level array like 1,2,3….
Now here comes an important observation in a full binary tree at any level, if I want to delete a subtree starting at node u the will need to delete 1 node from level[u], 2 node from level[u]+1, 4 node from level[u]+2…2^i node form level[u]+i.
Now form the data structure (here I have used Binary Indexed Tree(BIT)) just query the contribution of the deleted node subtract them form the total contribution of that level and take the maximum. We need to do this from level[u] to last level and we need to consider the whole level from level 1 to level[u]-1.