cerealguy's blog

MemSQL Start[c]UP 3.0 Round 1 Editorial
By cerealguy, history, 7 years ago, translation, In English

MemSQL Start[c]UP 3.0 Round 1 is over!

Congratulations to jqdai0815, Petr, eatmore and tourist on solving all the problems!

Here are our solutions:

Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +96
  • Vote: I do not like it

Comments Comments (30)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been translated by cerealguy (original revision, translated revision, compare)

→ Reply
»
7 years ago, # |
  Vote: I like it +95 Vote: I do not like it

In 859G - Circle of Numbers, it is possible to compute P(x) at multiple random roots of unity of degree n modulo multiple random primes of form kn + 1. If all the results are zero, the answer is probably YES, otherwise it is certainly NO.

By the way, my solution of G which I submitted during the contest doesn't use polynomials at all. It is based on Chinese Remainder Theorem. It can be easily explained if n is a product of two different primes, p and q. In this case, each point i on a circle can be mapped to cell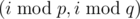 in a p × q table. The available operations are: adding the same number to all values in a row, to all values in a column, or to all values in the whole table. Now, the solution is simple: use the first operation to turn all values in the first column into zeros. Then, use the second operation to turn all values in the first row into zeros. Now, the answer is YES if and only if all values in the table are zero. When generalized to arbitrary n, the solution becomes more complicated, but the basic idea is the same.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I did something very close to the geometry interpretation, but I still don't see a convincing argument on why this works. I took every polygon with p vertices and ensured that the average value of the points on it equals to zero. When you do this for all p-polygons for p a prime dividing N, you either obtain all zeroes (which means that the answer is YES, and you also have a certificate for it), or not, and then the answer is NO.

    In the contest, I had certain intuition backed by stress tests (the approach is only prone to false negatives, hence is quite simple to check). But I failed to produce a rigorous proof both during and after the contest. Anyone has an idea?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +30 Vote: I do not like it

      I revisited this topic, finally understood the editorial and found the answer. The algorithm I used in the contest is indeed correct and I can prove it using statements from the editorial.

      We imagine the circle as a polynomial of degree n -- we take the exponents modulo n. For instance, when n = 5 then x2 * x4 = x1 as .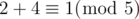

      What does multiplying this polynomial by xn / p - 1 mean in terms of the statement? It means that you subtract (in parallel) from each element ai the element ai - k (and rotate everything by k, but that can be safely ignored).

      When you subtract arithmetic mean of p evenly spaced points, this equals to multiplying by xni / p - 1 for all i in (0, p - 1), summing the results and dividing by p. We can safely ignore the case where i = 0, as this yields all zeros.

      The above is equivalent to multiplying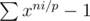 . Note that each term of this sum is divisible by xn / p - 1, thus the whole sum is too. The product of these polynomials for all p is 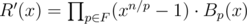for some polynomials Bp(x) (let's call them bullshit).

      We have .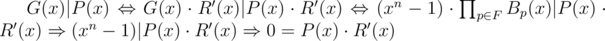

      The above in words means the following: if a solution exists then after doing all the steps, all coefficients will be zero -- the condition is necessary!

      Note that the reverse implication doesn't necessarily hold, because we are not testing divisibility by the "bullshit". However, the operations we've done are exactly the operations allowed in the statement (selecting some evenly spaced points and adding a constant) and they are reversible, hence we obtain a certificate for the result -- the condition is also sufficient.

      I am sure no one reads this anymore, but I nevertheless wanted to share it, as I am happy that my approach was indeed correct and not some heuristic that I was just lucky to pass with (although it is still true that I didn't have a formal proof during the contest).

      → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Could someone explain the first sample test for problem D?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    If we choose (1, 4), (1), then expected value will be 1 × 0.4 (for 1) + 1 × 0.55(for 4) + 2 × ProbablityOfWinning(1) = 1.75. Probablity of winning of 1 is 0.4 × 0.55 × 1 + 0.4 × .45 × 1 = .4

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    In the first sample, the optimal bracket is

     1
1 4

    So, the prediction is that teams 1 and 4 will win in the first round, and team 1 will win in the second round. In the first round, team 1 wins with 40% probability (0.4 expected score), and team 4 wins with 55% probability (0.55 expected score). If team 1 advances to the second round, it wins with 100% probability, so the overall probability that it wins the second round is 40% (0.8 expected score). The total expected score is 0.4+0.55+0.8=1.75.

    → Reply
»
7 years ago, # |
← Rev. 5   Vote: I like it 0 Vote: I do not like it

Is'nt solution for D just bruteforces all possible combinations and then returns the best option ?

What's the complexity for algo from this post ?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    You can't brute force since if we have 2^6 rounds, that means 64 teams, which is 64 factorial placements. Complexity of the algorithm is something like O(N^2*2^N) which is very reasonable with 2<=N<=6

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

"Another way to probabilistically test if the center of gravity is at the center is to choose a random prime p such that n | p  -  1, [...]"

Could you please explain how to find such a prime?

I tried generating random integers of the form x * n + 1 until I find a prime. It seems to be fast enough — in the worst case, for some n in range [1, 106], it required 123 attempts. Why does it work? In particular, I'm interested in answers to these questions:

  1. How can we prove that such a prime always exists?
  2. What range is best to choose x from?
  3. What is the expected number of generated candidates before a prime is found?

Is there maybe a better/faster solution?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it
    1. There is a theorem which shows that there are infinitely many such primes.
    2. It is better to choose smaller x (there are more primes among small numbers).
    3. Look at this theorem.
    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks a lot! That's exactly what I was looking for.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Commented Code for E That WAs on Case #8

Can someone explain what I did wrong and/or provide a countercase that shows the flaw?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    When I was looking through other sols to see if I had the right idea, to my surprise, Petr's sol seemed quite similar to mine, except for the way that we computed the size of our components. Is there an error in that area of my code in particular?

    EDIT: Now AC after changing the component size finding to a recursive DFS...

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

One liner for B
2*ceil(2*sqrt(n))
OEIS Minimal perimeter of polyomino with n square cells

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Wow, I thought that this is just a joke problem, but it has turned out there is much more to it:

    For certain classes of problems defined over two-dimensional domains with grid structure, optimization problems involving the assignment of grid cells to processors present a nonlinear network model for the problem of partitioning tasks among processors so as to minimize interprocessor communication. Minimizing interprocessor communication in this context is shown to be equivalent to tiling the domain so as to minimize total tile perimeter, where each tile corresponds to the collection of tasks assigned to some processor. A tight lower bound on the perimeter of a tile as a function of its area is developed. We then show how to generate minimum-perimeter tiles. By using assignments corresponding to near-rectangular minimum-perimeter tiles, closed form solutions are developed for certain classes of domains. We conclude with computational results with parallel high-level genetic algorithms that have produced good (and sometimes provably optimal) solutions for very large perimeter minimization problems.

    → Reply
»
7 years ago, # |
  Vote: I like it -7 Vote: I do not like it

Where are the author's solutions. They should be there !!

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem G, the alternate solution: I can prove that it's sufficient to check that the center of gravity is exactly the center for all such m. But I don't see why it's sufficent to check just m=1 (as long as you have sufficient precision)?

Can't it happen that the center of gravity is exactly the center, but it's not exactly the center if you rotate by some coprime m?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    If we define P(x) as in the problem, then the condition in question is equivalent to the nth cyclotomic polynomial P_n(x) dividing P(x). Now, it can be shown that the minimal polynomial of a primitive nth root of unity w is the cyclotomic polynomial. https://en.wikipedia.org/wiki/Cyclotomic_polynomial What this means is that if P(w) = 0 for a polynomial P, then P_n(x) divides P(x). Moreover, this condition is necessary and sufficient. In complex numbers, the center of mass is P(w) over the total number of points. Therefore, the condition "center of mass at zero" is necessary and sufficient.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain me how to solve Problem C with DP in detail? Thank you

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    i tried a bottom-up approach. my idea was: at i-th position let both of them decide individually whether they want the pie[i] piece. but there is a catch. person A will eat the i-th pie iff he/she is contented with person B's decision on giving himself/herself the total amount of pie till (i+1)-th position (from n). otherwise he/she will keep the token and let person B eat the pie[i]. let dp[i][j][k] (1<=i<=n,0<=j<=2,0<=k<=2) define the total amount of pie eaten by the person k (from n) till i while j has the token at i-th position.

    Code If Needed

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      thanks a lot

      but When its 2d dp we can visualise it by drawing, but how to do same with 3d dp? is there any method to verify that our 3d dp is filling in appropriate order?

      thanks in advance :)

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem E:

5
1 2
2 3
3 4
4 5
5 2

Many AC code outputs 2 for this case, but I think only the assignment [1,2,3,4,5] exists. What am I missing?

→ Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Its better to post this tutorial link on the home page blog. I thought the editorial is not yet published.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have the following concern regarding the solution for Problem D. When we calculate the scores namely, s[r][t], we first initiate s[r][t] = s[r-1][t] + p[r][t] * 2^(r-1) Then we find the maximum s[r-1][u] for certain values of u. My concern is that we are choosing the maximum s[r-1][u], but we don't consider it p[r][t] side. I mean for probability we take the expectation. We're conditioning on playing against certain u, but we don't consider that condition while computing the score, namely p[r][t] * 2^(r-1). Could someone comment on this?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I know it'd be an overkill, but just wanted to know for knowledge purpose, is F solvable using min cost flow algorithm?

→ Reply
»
3 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In problem G

(we were able to construct test cases where it was within $$$10^{-500}$$$ of the center)

How to construct test cases to make the center of gravity so close to the center?

→ Reply