Hello Codeforces,
I would like to invite you all to participate in the 2017 JUST Programming Contest 4.0 of Jordan University of Science and Technology. The contest was originally held on 16th of September , and it will launch in Codeforces Gym tomorrow Saturday 23 September 2017 14:30 UTC.
The problems were prepared by justHusam (Husam Musleh) and Vendetta. (Ibraheem Tuffaha).
Thanks to I-Love-Islam (Rami Sadaka) and The-Legend (Abdulmajeed Alzoubi) for sharing the ideas of two problems.
The duration of the contest is 4 hours, and the registration will be open 6 hours before the start of the contest.
Good luck for everyone, and I wish you all Accepted solutions.
Note: Don't forget to use fast I/O methods.
UPD: Registration is currently open. 
UPD: The contest will start in 30 minutes.
UPD: Tutorial










Should it be done in team or individually?
The onsite contest was made for teams of no more than Experts level, so a Candidate Master is preferred to participate alone.
Is "Scanner sc = new Scanner (new File (PATH))" considered as a fast I|O method in java ?
No. You need to use BufferedReader / PrintWriter instead of Scanner / System.out
timo14z Anemoi
How to solve A?
Hint: Consider bits one by one.
Solve for each bit independently:
Iterate through the array, and store the last position where the given bit was set. If we find some number where it's not set, or we reach the end of array, we have to consider how many subsequences contain this sequence of set bits. If there was X set bits, then there will be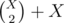 different sequences, so we have to add
different sequences, so we have to add 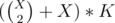 to the answer, where K is the value of the set bit.
to the answer, where K is the value of the set bit.
Sorry for the latency, you can check the editorial: http://mirror.codeforces.com/blog/entry/54840
Could you share F's tests, or it's generator please?
Why do you want to see the tests or the generator?
I couldn't figure out why my code was giving WA, but it's working correctly now, so never mind.
Can someone explain the solution for F ?
You can calculate the number of palindromic substrings for each string, and map strings, to their index. After that you reduced the problem to a max range query.
We calculated the no of palindromic substrings in O(30*30) time. Is it expected one ?
Yes, it runs fine, in case my solution passed in 1746 ms.
Can you share your solution please :)
https://ideone.com/U1GmWp
It's basically what bazsi700 explained, I counted the value of palindromes for every string, mapped the strings with a trie and used a sparse table to do the queries
Could you please tell me why I'm getting TLE on test 2 with this code? https://ideone.com/4TrlFW
I wrote I/O as you did to be sure it wasn't that.
Well, it's better to use sparse table and unordered_map in your code, but you would receive wrong answer because what calculate the length of a C string is strlen, since you are using sizeof, it's the same as to add the same thing for all values of strings. And you have to treat the case when l > r.
Yes I noticed the case when l>r, and I didn't know about strlen, thank you very much. But the TLE is because of the segmentTree factor which is a little bit worse than sparse_table?
Probably yes, try to optimize the query in the range and how you find the index of some string, I used a trie for example.
That only means O(104 * 30 * 30) ≈ O(107). If you are getting TLE, then other part of your code is too slow. You must use fast IO.
Sorry for the latency, you can check the editorial: http://mirror.codeforces.com/blog/entry/54840
Can someone give a hint on E?
Meet in the Middle
Think about divide and after join
for (n == 1) just compare element by element
for (n > 1) divide the set in two sets of same size and brute every combination in every set, and count how much times you can obtain every result in every set. After this, we can iterate in the values of set1 and find what value is necessary of the set2 that:
((valueOfSet1) * (valueOfSet2)mod(109 + 7) = = x)
You can use multiplicative inverse for this
And every combination and to answer the product of the quantity of how much every element appears in his respective set ( A basic combination). Complexity: O(67 * log(67))
Sorry for the latency, you can check the editorial: http://mirror.codeforces.com/blog/entry/54840