Hi all,
Let's discuss the problems of this contest.
How to solve problem E, F, G and I?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Hi all,
Let's discuss the problems of this contest.
How to solve problem E, F, G and I?
| Name |
|---|



Also C please
For problem C: Using dynamic programming that f[x] means the maximum speed when the current mass of rocket is x. enumerating the type and the number of the new stage is O(NM^2). But this can be optimized to O(NM) by saving the prefix maximum of f[x] - Isp[i] * log(x) for every type of rocket i and every mass x.
but how can we fix the order of the DP
I just sort all the engines by Isp from large to small , and double the engines by copyiny the same to n + 1, 2n. then do DP on it. Though I get AC, but I don't think it is correct
Here is another way to look at DP optimization.
When we add a stage with some drive type, we can put K >= Kmin drives of it. But instead of taking K drives at once, we can take exactly Kmin drives, and then add arbitrary number of same-type drives in special steps which follow. Then we need f[x] — maximal speed for complete rocket of mass x, and g[x, i] — maximal speed of rocket of mass x with last stage composed of drives of type i (which is not complete yet and can be extended).
Got:
Disk write error (disk full?).Hot to solve div-2. problem nr. 9 (Vim)?
F: First of all, you should be able to compute the volume of the region ax + by ≤ c, x2 + y2 ≤ 1, 0 ≤ z ≤ a1x + b1y + c1. I tried numerical integration during the contest and it wasn't precise enough. Got AC with closed formula in upsolving.
When a = cosθ and b = sinθ, by binary search you can find c such that the line ax + by = c equally divides the bread. Call it f(θ). Similarly, when a = cosθ and b = sinθ, by binary search you can find c such that the line ax + by = c equally divides (the bread + the butter). Call it g(θ). You want to find θ such that f(θ) = g(θ).
Notice that f(x) = - f(x + π) and g(x) = - g(x + π). Therefore, the signs of f(0) - g(0) and f(π) - g(π) are different. You can again do binary search to find a root in the interval [0, π].
I tried to compute volume with numerical integration during contests, but my output error was too big. (Even it couldn't pass examples)
I have a hypothesis(?) that planes which divide x2 + y2 ≤ 1, 0 ≤ z ≤ a1x + b1y + c1z region in half and perpendicular to xy-plane always through same point, But I can't prove it.
It's wrong, we checked it during the contest
Thanks for your advise.
I draw lines with GeoGebra and zoom in, then lines don't through same points. I was mistaken that I wasn't zoom in, and It looks does.
Interesting, so basically the cutting plane can always be a vertical one, right?
I want to share how to obtain a direction of the required plane in O(1) right after reading an input.
First of all, assume we have a unit circle, a linear function over it (say, Ax + By + C, let it be positive for convenience) and a line ax + by + c = 0. We want to compute an integral of the linear function over one of the parts the line divides the circle. We choose a parameter t, say that an one-dimensional integral over the chord parallel to the line and passing through the point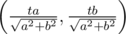 equals its length (
equals its length (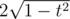 ) multiplied by the value at the center (
) multiplied by the value at the center (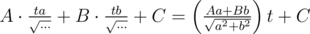 ), and our integral equals smth like
), and our integral equals smth like
It equals something like
the key observation to obtain it is to change t to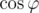 .
.
Our target is to find such a, b and c that this equals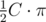 , or that the obtained linear function of A, B and C (the function above minus
, or that the obtained linear function of A, B and C (the function above minus 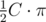 ) equals zero for (A1, B1, C1) (the bottom layer) and (A2, B2, C2) (the whole sandwich). This means that the obtained coefficients of this linear combination (
) equals zero for (A1, B1, C1) (the bottom layer) and (A2, B2, C2) (the whole sandwich). This means that the obtained coefficients of this linear combination (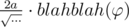 , etc) represent a vector which is collinear to the cross product of (A1, B1, C1) and (A2, B2, C2). One can easily calculate this vector once he has read the input.
, etc) represent a vector which is collinear to the cross product of (A1, B1, C1) and (A2, B2, C2). One can easily calculate this vector once he has read the input.
Let the cross product equal (A * , B * , C * ). Then obviously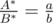 , so we just said that a = A * , b = B * and found c using one binary search, having handled cases when one or both planes are horizontal, this solution got accepted.
, so we just said that a = A * , b = B * and found c using one binary search, having handled cases when one or both planes are horizontal, this solution got accepted.
We tried calculate this volume by Simpson's rule. Looks like it was very close by precision, but not enough. Do anybody know, how this precision could be predicted before writing code? Error could be estimated by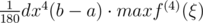 . But how estimate this derivative?
. But how estimate this derivative?
ruban (who created this problem) noticed that in this case order of convergence is different from classical, because the function being integrated has unbounded derivative at one end of the interval. More precisely, derivative of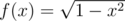 goes to infinity for
goes to infinity for 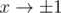 .
.
So the maximal value of derivative in your formula is infinite, hence the whole estimate is useless.
It's easy to calculate this volume if you notice that the integral of a linear function over some figure equals to the area of this figure multiplied by the value of this function in the center of mass of the figure.
5 (I think you meant this problem by E): what we really need to do is to find maximum number of music sheets that can stay in place. Sheets staying in place should form increasing subsequence in terms of pairs (number of composition, number of sheet in composition). Moreover, if one of sheets of same composition stays in place, then whole composition stays in place. Now let's do dynamic programming:
dp[y] = max number of sheets staying in place among compositions in range [0, y] if composition y stays in place(here we number compositions according to their order in input, let's call this source number (and let's call original numbers of composition target number). It is recalculated more or less as follows:dp[y] = max (dp[x] + (size of composition y))over all x that we have enough space to fit all intermediate compositions (intermediate in terms of target number) in segment between x and y (in terms of source number)`. This can be done with 2d segment tree that keeps values of dp[y] firstly by target number, then by second number: let's look at "free space" to the left of y (how many multifores to the left of y will remain empty if y stays in place) — it should be at least free space to the left of x for transition to be valid.So we reduced problem to 2d prefix maximum and point update — this can be done with 2d segment tree in time and
time and  memory. There are also some nasty parts concerning reconstruction of the answer, but basic is here.
memory. There are also some nasty parts concerning reconstruction of the answer, but basic is here.
Code.
You can reduce the problem to the standard Longest Increasing Subsequence problem. Take all the compositions ordered by number, and write down for each of them: its position minus sum of all lengths of compositions with smaller number. Now you need to find longest nondecreasing subsequence in the resulting sequence (add zero before start and M-N after end as sentinels), and it can be done in O(N log N) with ordinary 1D segment tree or Fenwick tree.
How to solve K ?)
11: There are two cases: UEF has no more than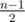 acquaintances, or no more than
acquaintances, or no more than 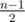 non-acquaintances.
non-acquaintances.
First case is just dp over subsets: for every mask of already listed acquaintances remember maximum possible number of new friends we can make and mask of people who stopped not knowing us already. Updating this when we list new acquaintances is kind of straightforward with bit operations.
Second case: notice that nothing changes if list some acquaintance second time, or if we already made all people who can theoretically start knowing us know us). We will try to find longest path in following DAG: vertices are subsets of our original non-acquaintances that still don't know Uef yet, but will start knowing Uef after he lists all his acquaintances; our acquaintances naturally correspond to transitions in this graph (subsets only become smaller as we do transitions, it does not make sense to take transition that does not change the mask). We found some way to list all our acquaintances that makes all people who can theoretically know Uef actually know him and best among such paths. There can be some repeats and some acquaintances not listed, we just will delete repeats and add all not yet listed acquaintances to the end of list.
This solution works in O(2kn) time and O(2k) memory, where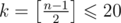 .
.
In fact the second case is also a DP over subsets, and a very similar to the first one. But we take as parameter of DP the subset of initially-unknown guys who we already know. It is important to notice that we don't need to store the subset of the guys we have already listed, since listing a guy many times does not change anything in this DP.
So the solution with two DPs over subsets is the intended correct solution.
However, I'm pretty sure someone managed to get recursive search with some pruning and dirty heuristics accepted. It was very hard to find tests which are not obvious for a search with pruning. Just push hard enough, and you'll be rewarded =)
Well, this DP is ok for both cases, if it's written as backtracking with memorization. All reachable states are unions of some subset of acquaintances, so they are limited by both 2#acquaintances and 2#non - acquaintances.
By this argument most of well-written recursive searches are really works fast.
Yeah, really fast, our is 9ms
Contest is over but submission is still
running.Run ID 1069.
Sent at 4:57:02. In resulting table it wasnt counted neither as wrong nor accpeted.
For problem 4(Universities), Is O(T * K) fast enough to pass? I got TLE on test 9.
You can optimize solution to O(nk) — it does not make sense to make day an entrance day if there are no students who apply to NSU on this day (be careful with case where nobody actually applies to NSU). Also double-check speed of reading input, because input can be really large.
Can someone write how to solve problem 4(Universities)?
Let us first calculate the expected gain of NSU for a given fixed entrance day t (1 ≤ t ≤ T).
Suppose, S = The set consisting of the students who applied to NSU.
Where,
P(i, t) = Probability that the i-th student will be available till the t-th day.
Gi = Value of the i-th student.
If you can calculate E(t) in O(K), then the total complexity of your solution will be O(TK) (as you can iterate over all possible valid t ). You can speed up the solution with this optimization.
How to calculate P(i, t):
Suppose,
C = The set consisting of the colleges where the i-th graduate has applied.
rij = The day on which the i-th graduate applied to the j-th college.
G(c, l, r) = Probability that the c-th college will have its entrance day between the l-th day and r-th day.
Then: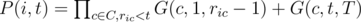
And 10(J) please
This requires high school physics/dynamics formula, like: v = u + at, s = ut + 0.5*a*t^2, v = d/t etc.
It is always better to have "higher acceleration". So sort the extinguishers by the acceleration parameters. Use one by one until you reach your goal, or run out of the extinguishers. In the second case, you will move the rest of the way in uniform speed (no acceleration)
Yeah, but i constantly received the wa6. Is there a problem with the overflow or precision?
I don't think so, if you have printed enough digits after decimal
When upsolving will be opened?
9(I):
Use fi, j, k to represent the shortest distance to current_row , current_col and start_row.
It is easy to deal j = k . When j ≠ k, we can find the path is from one position along some row's end, and it happens only
jorkkey used. So we have to handle the up and down when start_row is useful. My approach is to divide every nodes to two, one represents it is going to jump to some row with small length. When usekkey, it is possible for position (i, j) to go to the end of k row meets maxk ≤ t < i(length(rowt)) < j .Position (i, j) can go to the place where (i, j - 1) can reach, so we link (i, j) - > (i, j - 1).And we can use monotonic stack to reduce the edge to O(n). And another node represent it jumps to nearest row with same j.Finally, we can use shortest algorithm to get the distance and path.
So you use dijkstra to compute shortest path? and instead of the heap, we can use a link-list to maintain the current min because edge weight is small? I still worry that it will be too slow to pass, so I'll appreciate it if you could send me your code. thanks!