Given N. We can make equality with K numbers (can be repeated) like this:
(a1+1)*(a2+1)*...(aK+1) = N*a1*a2*...*aK
Find the smallest possible value of K for which there are integers that satisfy above equality
Sample 1: Input:4 --> Output:2 --> Explanation: Integers a1 = 1 and a2 = 1 are satisfying equation.
2 < n < 1000 TL: 0.1s ML: 64MB
I thought that the answer is phi(n), but that's just a guess.
Are you sure the answer is phi(n) because for n = 5, according to you the solution is 4, but i get a better solution as 3.
(1 + 1) * (1 + 1) * (4 + 1) = 5 * 1 * 1 * 4.
Although, I am still not able to come up with full solution, I would like to know what the source of the problem is?
Thank you for the test, I couldn't find solution for n=5 so phi(n) was just a guess. Problem is from competition that is held in faculty of mathematics in Serbia. Competition is matf++ 2016, but you need to translate page.
Try dynamic programming. dp[n] will be the answer for the original problem. To calculate it:
The idea is to try every divisor of n to start the left sequence. Now you have to solve a smaller problem where you'll want to find the same sequence for:
EDIT: this solution is incorrect, as pointed out by ABalobanov. Since you don't depend only on previous states you cannot build this dp direclty. You have to do something like ivan100sic proposed.
I think d + 1 is not neccessarily the divisor of n.
This is the actual source of the problem (Task A3):
http://www.math.bas.bg/keleved/shumen2010
I solved it by doing a breadth first search over all rational numbers whose numerators and denominators are not too large (up to some M, I used M = 20000), starting from 1, and at each step multiplying by a number of the form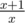
until I reached N. The value of K is actually always quite small, no more than 14 for n < 1000. You can just run this BFS on your own computer and store the solution as a string since there are not too many different inputs. I have no idea why the value M = 20000 is sufficient.