The problem is: given an array of size n(n < 2 * 10 ^ 5) of integers(a[i] < 2 * 10 ^ 5) and 2 types of queries. The first one is to assign a value to an element(v < 2 * 10 ^ 5), another is to find such minimal k that k >= i and a[k] >= x(i and x are given and lesser than 2 * 10 ^ 5 both). I wonder how to solve it faster than O(nlog^2(n)).
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
3 days
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
3 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 2 | maomao90 | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/20/2024 12:24:40 (g1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











You can solve it in NlogN about the same way you solve it in Nlog^2. You keep a segment tree with the maximum on each segment, and then when you need a certain position you can instead of binary searching it, go directly to it through the intern structure of the segment tree. For example, let's consider how the interval [i, N] is decomposed in at most logN intervals maintained in the segment tree, in order of their appearance. Now, you can iterate over them: the position you're looking for is part of the first segment with a maximum value of at least how much you need (that is x). So far you had O(logN). Now all you have to do is to find the first position in this interval with value greater than x (such a position exits as the maximum would be fine — we already checked that). So you can go downwards starting from the segment, always choosing the left child if that one has a maximum of at least x, or the right one otherwise. That would be logN+logN -> O(logN) complexity for querying.
Thanks
Can you provide a implementation for this?
Why are you asking? What's your concern?
We can maintain a segment tree of maximum values and do it in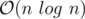 . Suppose, we have to find next greater element for range [i + 1, n - 1] for index i. Let us suppose the maximum of range [i + 1, n - 1] is less than a[i], then we don't have any next greater element and we return - 1. Otherwise, check the left half and right half of the range [i + 1, n - 1]. If the maximum in left half is ≥ a[i], you'll go to the left half in the query function of your segment tree, else you'll go the right half of your segment tree.
. Suppose, we have to find next greater element for range [i + 1, n - 1] for index i. Let us suppose the maximum of range [i + 1, n - 1] is less than a[i], then we don't have any next greater element and we return - 1. Otherwise, check the left half and right half of the range [i + 1, n - 1]. If the maximum in left half is ≥ a[i], you'll go to the left half in the query function of your segment tree, else you'll go the right half of your segment tree. 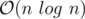 only.
only.
Now, how to implement this? Well, our range [i + 1, n - 1] actually consists of disjoint ranges in segment tree, so you'll go to the leftmost range which lies in our original range, check for the above conditions there. If it doesn't satisfies, we will return - 1 and we don't have to go to further down the segment tree. If the leftmost range doesn't return - 1, we don't have to go the other ranges which cover [i + 1, n - 1], so overall complexity is
Nice discussion of ongoing Codechef long contest problem
Ahh. Now I understand why this was so downvoted=)))It was an almost classical problem that not everybody knows the solution for, so I thought it's a really nice blog as it gives other the chance to learn something. Couldn't the guys who downvoted say here so that I didn't comment? It's really stupid just to downvote and not hint out that you shouldn't answer the blog.