UPD: Editorial in Vietnamese: http://acmicpc-vietnam.github.io/2016/regional/solutions/ACMICPCRegionalVietnam2016-Editorial.pdf
Hi all,
On Oct 15th, 7pm Vietnamese time, we will have Vietnamese regional 2016 replay on Kattis.
- The contest will last for 5 hours with normal ACM ICPC rules.
- After the contest we'll publish editorial in Vietnamese and official solutions.
- Teams are recommended.
- It is not rated.
If you are not afraid of spoilers, see standings here. Team from Seoul National Univ were #3 in ACM ICPC World final 2016-2017 and LINUX from VNU were #39 in World final 2016-2017. Can you beat them? :p
The problems were prepared by I_love_Hoang_Yen, ngfam_kongu, lythanh, khuebeo and some professors in Vietnam. The contest is uploaded to Kattis by I_love_tigersugar.











Could you please remove the LINUX's position from your blog post so that members of that team don't feel ashamed of their terrible performance at World-Finals-2017? :'(
Infact after your comment, people would be more curious to see their team (LINUX VNU whose rank was #39 in icpc world finals).
39 at WF is fine. Just accept your past.
What I get for problem I:
Call f(x) the number of times that we can replace x which x / p where p is a prime. Then number x is equivalent to a pile of f(x) stones in a Misere game. The whole problem reduced to finding the number of subsequences such that their exclusive-or sum is 1, which is an easy DP problem.
What I didn't is that how to compute f(x) quickly (and I think most of the teams stuck here, too). Any idea?
You can solve it like this: To calculate f[x]: For each prime <= 10^4, you can brute-force to count this part, and divide x for any of them. After this, any prime divisor of x will > 10^4, so x have at most 2 prime divisor. Use something like Fermat's little theorem or Miller–Rabin to check if x is a prime, then you're done.
There are 1229 primes < 10^4, so I think this algorithm will have enough time to run. You can also do something like stop trying if x is greater than current prime^2, have a table for x<10^6 so you can look it up whenever x<10^6, ... . Because all the number we care about is >=a and <=b, so it's hard to give a and b such that it's take too long to calculate the whole sequence.
Despite saying all that, I can't guarantee that this algorithm will pass. And I couldn't come up with your idea :(.
Let g[x] = x for x = [A, B]. For each prime p ≤ 106. Find the smallest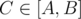 st: p|C and do as follow:
st: p|C and do as follow:
Nice approach.
i found out the way to calculate f(x) but didn't know about misere :(
That Van Hanh Pham solved 10 out of 12 problems and the 2 problems he did not bother to solve are those almost everyone could solve. Does that means he alone could beat the best team from Seoul National University?
He's I_love_tigersugar, contest uploader.
As above comment, he is contest uploader. He submitted to test author solution, time limit and judge programs. We tried to hide him from scoreboard but could not.
Is there any way to see the running time when submitting as a spectator?