Let's discuss problems.
How to solve E ?
Someone solved B without precomputing the answers ?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Let's discuss problems.
How to solve E ?
Someone solved B without precomputing the answers ?
| Name |
|---|



I’m interested in E, I, J.
E: We got [continued fraction] of input and tried all of the prefixes
Can you explain what that means?
click
How much prefixes did you use? Did you use long arithmetic? I've got TL6 when tried to check first 50.
Assume that we know that
Then there are several cases:
If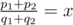 (this equality should be checked precisely since, for example,
(this equality should be checked precisely since, for example,
1/(1e9) = 0.000000001000000000, and1/(1e9 + 1) = 0.000000001000000001), then the problem is solved.If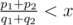 then we find the maximal t for which the inequality
then we find the maximal t for which the inequality
holds. If we just say that $t = 1$ then we get TL (remember
1/1e9?).If
>, then similarly.Very fast and simple implementation of this idea:
all of them. There's
O(log Precision)of them because it's like Euclidian algorithm.Why is it correct?
My solution is to do a binary search using Stern-Brocot tree. The depth can be O(n), but the number of turns (move to the left son, then to the right or vice versa) is and we can find the next turn in
and we can find the next turn in  time using binary search.
time using binary search.
Can you please explain why it's not the same?
Wow, I've never thought that these two concepts are such closely related.
Well, honestly I don't have a proof for that.
English wiki claims the following, but I don't want to trace sources
One can choose to define a best rational approximation to a real number x as a rational number n/d, d > 0, that is closer to x than any approximation with a smaller or equal denominator. The simple continued fraction for x generates all of the best rational approximations for x according to three rules: ...
During contest we stresstested it
We actually don't check one of the cases (when last number in fraction is even), so this might be incorrect-but-passes solution (:
I: Suppose right(i, j) — answer of testing system about vectors i,j.
First of all, lets find 'min' (in quotes, because if answer is NO all vectors satisfies this condition, but we will check it further) vector — at the start suppose min=1, and reassign it to j if right(j, min) over all j. After that we can split all vectors to the three lists 1. such j, that right(min, j) == 1 2. such j, that right(j, min) == 1 3. right(min, j) == 0 && right(j,min) == 0
If the second list is empty, answer YES -> Sort first list, and concatenate with third. Otherwise answer is NO -> sort first list, sort second list, and print concatenation of first, third, and second lists.
How to sort lists? Just with builtin sort with overriding comparator which makes queries to the testing system. (it can be done since we divide vectors to three lists — to the right/to the left/opposite towards to 'min' vector)
Yeah, that was one of the intended solutions.
Note that the vectors are guaranteed to be pairwise non-collinear (we thought the problem is good enough without corner cases), so we don't actually need the third list.
I: I will call that point a less then point b iff the interactor answers 1 for it. This "less" is not necessarily transitive.
lets fix one point and divide all others into two parts: those that are smaller than 1 and those that are greater.
Now in each half we can sort them using std::sort with comparator that ask interactor since it will be transitive since each half represent a halfplane.
Now we got an array to print [all less first in sorted order], fixed point, [all bigger] in sorted order. Answer is yes if the first point is less then other and no otherwise. Note that we always have k=n when printing the answer
J:
First of all — sort b, after that you need to find first number in answer with binary search (for fixed X, we can count how much numbers a[i] + b[j] <= x via 2-pointers or another binary search). Suppose this number is X, answer will starts with several X numbers, and then will increase, we will take all X-prefix immediately, and then do following: for each a[i] we need find min j (lets call it next[i]), that a[i] + b[j] > x (it can be done with 2-pointers or BS like before). And then we should collect all a[i] + b[next[j]] in priority queue (PQ) and pick remaining numbers from PQ — when we pick a[i] + b[next[i]] from PQ, we need to increase next[i] and if possible — add new a[i] + b[next[i]] to PQ again.
E: We got OK with a solution on a python in 7 lines.
wow
How to solve D?
+, we asked our friends after the contest, they all told solutions which doesn't actually seem correct (especially with such a strict constraints), and ofc nobody knows how to prove it, so I wonder if there is a proof of the solution.
The sketch follows: build a graph which has traffic lights as its vertices and there is an edge from u to v with length len iff for some event their numbers differ by len, then we print the gcd of all cycles.
My main question is: why there is the only answer? Maybe I misunderstood the solution, though.
That looks right. However, the
gcdpart is not needed if we just search for the shortest cycle instead of all cycles. Please see my comment describing a solution (in layman's terms, which adds length but hopefully tells more about correctness).Here is a solution for problem D. It has a long-ish explanation because it uses problem-specific concepts rather than a more rigorous and concise mathematical model, but that actually helps to better show its correctness.
Let us start with an example of the real system behind the test (the problem statement guarantees that the traffic lights at a crossing are behaving as described). The numbers are scaled down a bit to aid readability. I'll just list all observable states. The period T is 10 seconds.
We are given several such observations in an unspecified order, for example:
For any two distinct observations, if they have numbers in the same column, we can conclude that one can happen a certain number of seconds after the other. For example, when we have A =
X 3 5 7and B =X 2 4 6, we know that B can happen 1 second after A. (Or it can be T + 1, 2T + 1, ... seconds, but we will be interested in the minimum such number, so T is not involved.) On the other hand, for observations P =X 5 7 Xand Q =3 X X 2alone, we can not say what can be the exact number of seconds between them.The solution will try to reconstruct a possible order of observations. First, pick any given observation. Then, repeatedly find the nearest possible observation which could happen after the current one, and proceed with it. Here's how it goes:
X 3 5 7, the nearest is B =X 2 4 6which can happen 1 second after it;X 2 4 6, the nearest is E =4 X 1 3which can happen 3 seconds after it;4 X 1 3, the nearest is D =1 6 X Xwhich can happen 3 seconds after it;1 6 X X, the nearest is A =X 3 5 7which can happen 3 seconds after it.When we arrive back at A, we can add up the number of seconds between consecutive observations in our sequence, getting 1 + 3 + 3 + 3 = 10.
Now, obviously, since we moved only forward in time, the number we found is a multiple of T. Turns out that, since we always picked the nearest possible next observation, it is exactly T. Let us see why.
Suppose it is greater than T (at least 2T), then we somehow jumped over our initial observation A at least once. For example, say we jumped from D =
1 6 X Xright to B =X 2 4 6. Now, a move from D to B was supposedly valid because of the second column: 6 changed to 2. The information contained in D and B allows us to determine what happens in the seconds between them:It is important here that each light changes its color exactly twice during the period T. This means that, when we see
? 3 ? ?and we have A =X 3 5 7, we can conclude that they are one and the same: of the T possible observations, there can be exactly one with the number 3 in the second column. But then A was closer to D than B, and we were able to determine that by the numbers in the second column: 6 - 3 is less than 6 - 2. So we were wrong to pick B instead of A as the next observation, which completes our proof by contradiction.So, if we got back to A, we found the period. Let us see now what happens when we don't get back to A. For example, if we had no observation E, only the first four:
Then we eventually come to a halt:
X 3 5 7, the nearest is B =X 2 4 6which can happen 1 second after it;X 2 4 6, we can not find any nearest observation.Now we shall prove that T can not be determined. Recall what are the real states of the system, and what part we see:
As we can see, actually, the next observation after B would now be D. Here is what we know by looking at them:
Nothing we observed prevents the system to have any number of lines just above D, for example, the following three lines:
As the number of such lines can be arbitrary, the period T can not be uniquely determined.
The implementation is actually a few times shorter than the textual explanation above.
This solution can be formulated in terms of graphs: observations are vertices, we draw edges and search for the shortest cycle. But in graph terms, it is harder to see which strategies of searching for the cycle actually yield the shortest cycle and which don't, since some problem specifics are easily lost when we use the graph model. And it is harder yet to prove that no cycle means no solution.
Another graph-oriented solution is to see individual lights as vertices, and construct an edge between two lights when they are both red in some observation. This approach also leads to a correct solution, but the proofs are also not obvious.
D: It seems a very simple solution passes. The answer is the maximum g such that there exist x1, ..., xm and y1, ..., yn such that xi + yj ≡ ai, j(modg) for all (i, j) (here ai, j is the (i, j)-element in the input). If we can satisfy the equations without modulo, the answer is - 1.
Does anyone have a proof?
Golovanov399's question becomes the following: why is g the only answer (and g's other divisors are not)?
If we work on some examples, we can at least get the intuition why this seems correct.
112
121
In this example, g = 22, but even g's second largest divisor (11) is too small because 12 appears.
X18
18X
9X1
This time, again g = 22, and 11 may look good, but actually the top-left corner should be 16 and 16%11 is too small.
Well, I've heard also that the answer is not unique if there are multiple connectivity components. I also can't understand why, for example, if the gcd of all cycles is a prime number, we can't obtain that it's the answer.
No, we don't need to care about the number of components. Simply compute the gcd of everything.
If there's no nonzero cycle, we can easily prove that a sufficiently large number is always a good modulo.
It means that either I misunderstood one of the solutions or the tests are weak, and the latter makes the fact that this whole solution is incorrect pretty possible.
This seems right, here is my attempt to prove it.
Consider the real period of the system, T. In this solution, xi are something like the moments of observations modulo T, and yj are something like the moments of switching lights to green modulo T.
Now, if actually g = T, such xi and yi exist by definition.
If T can not be uniquely determined, it turns out (*) it is actually because the system can be altered so that T is increased, but no observations are changed. In terms of your solution, it means the equations can be satisfied for arbitrarily large g.
The remaining question is as follows. Suppose the value T of the real system actually can be uniquely determined. Let g > T. Why the equations can not be satisfied for such g?
Note that the values ai, j are all lower than the real period T, and so lower than g. Let us then rewrite the equations as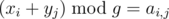 . This way, it is obvious that, if they are satisfied, g can be the period of the system: it describes the system with moments xi modulo g for observations and moments yi modulo g for lights turning green, and such system can give the exact same list of observations as the real system with the real period T. This contradicts our assumption that T can be uniquely determined.
. This way, it is obvious that, if they are satisfied, g can be the period of the system: it describes the system with moments xi modulo g for observations and moments yi modulo g for lights turning green, and such system can give the exact same list of observations as the real system with the real period T. This contradicts our assumption that T can be uniquely determined.
(*) Please see my other comment describing a solution, where this property is established in the process.
B: For every perfect square that has the same number of binary digits as n, check if it has the same number of ones as n. Runs in ~ 1 second.
E: Use solution for problem from here.
B: Do I understand correctly that you iterate over all squares in range [2^x; 2^(x+1)) for appropriate x? So, it's O(sqrt(N)) solution?
Yes, it's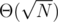 with a really small constant.
with a really small constant.
I'd like to thank authors for problem H, I think this's the most beautiful problem of the contest (especially comparing to D and F, not sure about F), despite it wasn't correct until the last hour. I want to share our solution (or at least its sketch):
Assume the graph is a tree. Run dfs which for every vertex will perform some derivations and return an id of a disjunct which has the only literal corresponding to the edge from this vertex to its ancestor (either its variable or its negation). It can be obtained by resolving some declared disjunct by the obtained literals for all descendants. After we do it for root, we get the empty disjunct.
Now if there are some edges not from the spanning tree, we do literally the same, but after this we have a disjunct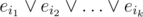 , where ij-s are the ids of all edges outside of the spanning tree. For every j we eliminate eij from this one by one: consider any cycle with this edge and having all other edges in the spanning tree, and map all these edges' variables to their negations (other variables remain the same). Then resolve two last disjuncts by the considered edge.
, where ij-s are the ids of all edges outside of the spanning tree. For every j we eliminate eij from this one by one: consider any cycle with this edge and having all other edges in the spanning tree, and map all these edges' variables to their negations (other variables remain the same). Then resolve two last disjuncts by the considered edge.
One can see that this takes exactly 2m + 1 operations.
How to solve problem F?
btw: It take me more time to understand H than solving this one :(
I cannot call what we did a "solution", but nevertheless.
First, note that we know the exact position of the robot d steps ago. Since we know it, we may find the set of positions where the robot may be now: we just emulate last d commands, splitting the possible position in two if there is no information about the corresponding wall (kinda nondeterministic automaton).
Once we have this set, let us define its score as the average length of the shortest path to the target cell. The shortest path is "optimistic": we run BFS which makes the move either if the wall is known to be absent or if nothing is known about it.
Finally, on each step we make such a move that minimizes the score of the set that will appear after this move. The intuition behind: we want the robot to be as close to the target as possible, but the best we can do is to do it on average.
This alone was not enough to get OK. To grab it, make each k-th move at random. We tried several random k at the very end of the contest (that's why +8). 6 and 30 passed, 10, 15 and 20 did not. It shouldn't really matter, most likely it was just a matter of luck.
Probably the solution may be improved by noticing that each position in the set has its own probability. If we say that each unknown wall exists with probability (number of walls left to place) / (number of unknown slots), weighted average would make more sense.
I had a similar approach, but with two differences: 1) Instead of finding the set of positions, I just picked a random 50% yes/no answer for unknown moves (only once per move, i.e. as long as the move stays unknown my guess will not change). 2) Instead of trying to go as fast as possible to target cell, I was going as fast as possible to the closest way to get new information (i.e. try to walk through unknown wall). This allowed me to avoid the "optimistic"/"pessimistic" question.
I've just changed part 2) to your approach, and my solution actually improved: as submitted on the contest it was making ~5500 moves on average, and now it makes ~3000 moves on average.
So it seems that somehow picking a single random assignment is better than finding the set of possible positions. The reason seems to be the following: it allows me to treat the same wall consistently — I guess in your approach, if we walk through an unknown wall twice, you will branch twice independently, and thus have some truly unreachable states, while in my solution I take a random decision on the first visit and remember it, so the end state is definitely possible. I've tried removing the "remembering" part from my solution, and the number of moves jumped from ~3000 on average to ~7000 on average, regularly exceeding 10000, which seems to confirm your contest experience.
Just checked that picking random answer once per move is also not an improvement: I've changed the solution to pick unknown answers randomly every time (but still consistently within one step), and it improved to ~2500 moves on average.
So it seems that only the "consistency within one step" idea actually helped me get the problem accepted.
About problem F.
Sure, in any solution, we have to move around, maintain our known position, and fill a map of the maze when walls and passages become known. The main challenge is how to behave when we move in uncharted territory.
For this, the idea of the author's solution is as follows. The problem statement explicitly defines the maze generation process, which is informally known as Kruskal's algorithm for maze construction. The solution just constructs random mazes using the same algorithm. In uncharted territory, we behave as if we were in the maze constructed by us. This way, we always know where we want to go.
Here are the details. Construct a maze X which is consistent with the known map (start with the known map, shuffle the unknown edges, run Kruskal's algorithm for them). Solve it: find the path to the goal. Start moving along this path. Now, two things can happen.
First, at some point of time, we can learn that some passage in our maze X is actually blocked by a wall. Then we construct another maze consistent with the new information. There, we replay the moves for which the result is not still known. After that, solve the new maze and proceed to move along the path we found, just the same as before.
Second, we may reach the goal in X, assuming that we miraculously guessed the maze. Just the same: construct another maze, replay the moves, solve it, proceed. Take care here: when we are almost at the goal, many mazes we construct will appear already solved. So, if the newly constructed maze is solved already, we can just make a random step.
This alone gives an average of 2700 moves, with one or two outliers of 5000 + ε moves among 100 maximum tests. Some tweaking, like considering several mazes X at once, get the average below 2100 moves, but the difference was not enough to consider these a major improvement, so we thought the limit of 10 000 moves will be fine. This naturally allows some other approaches as well, and I'm delighted to see ifsmirnov and Petr already shared theirs.
For illustration, here is an example state of the map after ~1500 steps:
Note how all
?s except the upper right corner of the map became irrelevant at this point: no matter what the real maze is and which maze X we construct, we won't have to go there since they are cut off from the goal.Btw can we see (if yes, how) the problems of the current season if we don't have an opencup login?
I believe one cannot.
Coming late to the party, our coach found this article wrote by Patrascu, explaining E:
http://infoweekly.blogspot.ro/2007/10/rational-search.html?m=1
What is very interesting about this article is that he proves that if you do "galloping" binary search on the fraction tree (which I assume means binary searching with increasing and then decreasing powers of 2), you get O(log(numerator)) complexity for any binary search on fractions, instead of the expected O(log2(numerator)) for regular binary search. That's pretty powerful.
Indeed, I submitted 2 solutions. The one with the normal binary search takes 500ms, the one with the "galloping" binary search takes 100ms. Incredible.
How to solve A?