awoo's blog

Educational Codeforces Round 33 Editorial
By awoo, history, 7 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +58
  • Vote: I do not like it

Comments Comments (64)
| Write comment?
»
7 years ago, # |
  Vote: I like it +28 Vote: I do not like it

What about using a persistent segment tree for F? We let version=depth and it should run in .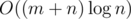

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I'm assuming that by version = depth, you mean that T[i] in the k-th version will contain the k-block minimum for the subtree rooted at 'i'. Persistent segment trees get their memory and time complexity based on the fact that each version differs from the previous one by 1 position ie., O(LogN) nodes in the tree. But, in this case, the minimum for k+1 can be different from the minimum for k at every node.Correct me if I got it wrong, if that is not what you meant.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it +4 Vote: I do not like it

      I was struggling with that for a while too, but since you can reindex the nodes in DFS order, keeping track of entry and exit index, before putting them in segment tree, it guarantees logn. The key thing is the segment tree is balanced even when the original tree isn't. Here's my submission: http://mirror.codeforces.com/contest/893/submission/32605016

      EDIT: My bad, I didn't read carefully. The k-th version is all nodes with distance <=k from the root (using placeholders +INF for all the other nodes)

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

how to solve 3rd question rumor

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This is my solution to this problem i did it as described in the editorial, i took given members as nodes and friendship between a pair of members as edge and constructed an undirected graph and simply traversed each connected component using bfs and took the minimum value of member from each connected component and added it to answer

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      An integer isn't always large enough to contain the final solution, as it can be up to c*n, which is 10^14.

      → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

in E — in O(1) (by precalcing factorials and inverse factorials)

https://en.wikipedia.org/wiki/Stirling_numbers_of_the_second_kind

in order to solve the problem you had to calculate s(n,k). How can you calculate this with O(1)?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think he means you can query/access value in O(1), but I'm sure the time to precompute takes longer.

    → Reply
»
7 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Can someone please explain Div 2 F ? I am not able to understand it from the editorial ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I made it using something like merge-sort tree. First, you need to do a dfs(euler tour tree) to store the time you processed the vertex u, store the depth of u and the size of subtree. Create an array V[] that on each position V[time[u]] stores a pair containing the depth and the cost of vertex u(V[time[u]] = <depth[u], C[u]>). Now, Build it like a normal segment tree, but each node keep an array that stores all the elements of V in the range(L,R). You can see that only O(nlogn) memory is used to store them. Do some preprocessing on the nodes of the tree: for each position i of the array of each node, do array[i].cost = min(array[i].cost, array[i-1].cost). Now, you just need to do a query on the segment tree: find the interval [time[u],time[u]+subtree_size[u]], and do a binary search on the array stored on the node searching the last value of depth less or equal than K and return its cost. Since we made that preprocess before, this cost will be the cost of the minimum cost vertex of the k-blocked subtree of u. I hope you understand, my english isn't that good.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +3 Vote: I do not like it

      Can you elaborate the pre -processing part? Also, can you explain the over-all logic behind your code?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +4 Vote: I do not like it

        The pre-processing: The answer for the k-blocked subtree of u is the minimum between the answer from 1-blocked to k-blocked subtree of u. So we need to get the minimum value c1 that has distance not more than k from u. Since the data structure is holding , in each node, an array containing pairs like <depth, cost> sorted by depth, we just need to propagate the minimum answer found to bigger depths in that range. Thats why i pre-process every node, to make this prefix minimum operation. Now, how do i know i am querying the subtree of u? Using time[u] (from the first dfs), we know that for all v with time[v] <= time[u]+subtree_size[u], v is in the subtree of u, so when i call my query to get the answer from time[u] to time[u]+subtree_size[u], with depth K+depth[u], i'm getting the minimum answer for the subtree of u. When i find the range of subtree of u, i do binary search on the array, getting the last pair <depth, cost> with depth < K+depth[u] (if depth[v] -depth[u] <= K, then v is on the k-blocked subtree of u). Since i made that prefix minimum operation in the array, the last pair satisfying the condition gives me the minimum answer for that range.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +3 Vote: I do not like it

          Can we build a segment tree inside every node of the original tree, to get the minimum cost, in the given range?

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            I believe would just be a 2D segment tree. But as the editorial says, it might be too slow since querying would be O(lg^2 n).

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              I solve using sqrt decompositon which answers queries in O(sqrt(N)), so I think, as editorial says, O(lg^2 n) per query is OK.

              → Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Problem C can be solved using disjoint set too!

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    it is saying TLE .I have used disjoint set .55217078

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You are missing the path compression. Your parent function has $$$O(n)$$$ complexity.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone elaborate on solving Problem C. I understand that if we find the minimum of each group, it will give us the minimum gold in order to spread the rumor. However, how can we turn the list of pairings we are given as inputs into groups?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Build an undirected graph. If there is a pair (u, v) then there is an edge from node u to node v and from node v to node u. Two nodes are connected if there is a path between them.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can build a graph from the list of pairs of friends. Then, every connected component will be a group. Run a dfs for each group and keep the minimum value from it. Sum this value to the ans after finishing a dfs on one group. Another solution(mentioned by the guy above) is to use disjoint set union. For each pair (u,v) , merge the group of u with the group of v, storing the minimum value for that group. Now just iterate over all disjoint groups adding to the ans the stored value for each group.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks, your explanation was very clear. I'm still having trouble with the "Every component will be a connected group" part. How do you represent these groups? For example if 1 is friends with 2 3 4, then my adjacency lists look like:

      • 1 : [2, 3, 4]
      • 2 : [1]
      • 3 : [1]
      • 4 : [1]

      But if I DFS starting with every node, I will find the minimum, but I will be quadruple counting this one group. Sorry if this seems silly, I am pretty new to graph problems.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        You could use array of boolean to flag which node/vertex already visited. So it looks like this:

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain me please why C(y+cnti-1 ; cnti) is the corect formula? I can.t undertand from where we have this relation

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Good Contest

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain me "Segment Tree structure" solution for "F" ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hi, i explained my solution using segment tree here (on this same post)

    → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Can someone explain to me why my solution for D is wrong? https://paste.ubuntu.com/26042298/

For each ai = 0 I supppose that I deposited the maximum amount of money that I am allowed to deposit. Then, if my money at bank is greater than d, I substract only the necessary from the last deposit; if after this update, my last deposit cant make my money at bank non-negative, print -1.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Accepted!

    I was missing something important!

    You can check my solution here: 32652462

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hi, what should be the output for 4 10 -10 -10 -10 0

      Your solution gives output as 1. I think it should be 2 with final solution as 10 -10 10 0. Am I missing something here ?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        In the given input they will check our account balance only last day.To make sure the money we have in the last day is non-negative, she should go to the bank in the last day and deposit some money between 30-40. Because she has -30 and the limit is 10. Answer is 1.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone provide a proof for editorial for E?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

893F can be transformed into a 2D RMQ without assignments where there's only one element in each row, so I think 1D Sparse Table + 1D persistent segment tree/balanced tree can be used, which could also run in O(n log^2 n + m log n)... (Note: let dat[i][j] be the segment tree for elements from the i-th row to the (i+2^j-1)-th row, then the difference between dat[i][j] and dat[i+1][j] is only about two elements) Yet I'm not certain whether this solution will get Memory limit Exceeded. [sorry for my poor English]

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain the example input of F, why the output is "2 5"? I think I misunderstood the problem somehow...

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

In Problem C — Rumor, the editorial and comments mention describe a solution where one takes the sum of minimum gold for all connected components. In my solution 32587668, I sorted the characters by the amount of gold they need to spread the rumor. Then it is sufficient to process each character in order and run a DFS if not visited and sum up the gold required. There's no need to take the minimum anymore.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem E for every prime divisor i of n , we are calculating the number of ways of putting 'cnti' objects into 'y' boxes.

Or in other word the number of non-negative integral solution of equation x1+x2+x3+....+xY = cnti.

And this should be equal to (cnti+y-1)C(y-1) .

What is wrong in this logic? And if it is correct then how that formula came which you wrote over there?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For f we can also use fractional cascading wich gives us a solution with (n+q)log

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have a solution for F that involves a 2D data structure (It's a Segment Tree with Treaps in each node). It runs in O((N+M)*Log^2(N)). Here's the submission: 32671104

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hello codeforces community .. can someone tell me that the rumor problem can be solved without using the dfs / bfs i am just trying to maintain the neighbours of each vertex in an vector of vectors but get stuck any help will be appreciated

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone post their approach for the problem D (Credit Card) in Div 2?

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Maybe I am too late to answer this, if not, it can be helpful . The first idea we get is , maintain a sum, till ith number, if corresponding query is check , and sum is less than zero, increment out result by 1. But that's not true. Example 7 7 -1 0 -1 -1 -1 0 -1 we may answer it 2 , by the greedy approach explained , but answer should be 1.

    So how we actually solve this ? Well, instead of trying to add the smallest possible number, we should try adding the largest possible, such that , the total don't exceed the given limit at any index . So , while we are at an index having 0(check) We find the maximum value we can add to current index, and hence all elements after this, such that limit is maintained. We need to answer range max queries , on prefix sum array You can use, sparse table or any other data structure for this.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Actually, tests in F are really weak. I got AC with O(n) for minimum query (with default athor solution which is supposed to use sparse tables to process a query with O(log(n)) by going down from x with 2^k steps and taking minimum on segment of precalculated values each time).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In E, can someone explain this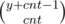 ? And why do we multiply answer every time when we encounter new prime?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Imagine each element in the array as a box, so we have y boxes with us. Now suppose we have 2 as a divisor and our number x is divisible m times by 2. So now we have m 2's which we can put in any of the boxes. So how do you arrange m (balls) into y (boxes) ? See here for the formula: https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you!

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        I got the first part(stars and bars one), but why do we multiply answer every time when we encounter new prime?

        upd: i got it now.

        → Reply
        • »
          »
          »
          »
          »
          5 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          can you explain it to me why we are multiplying?

          → Reply
          • »
            »
            »
            »
            »
            »
            3 years ago, # ^ |
              Vote: I like it +1 Vote: I do not like it

            Can anyone explain it to me now? Why not we count the occurrence of every single prime first and then use stars and bars formula? Why multiply every time we encounter a new prime?

            → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Can someone tell me why my submission gets MLE in problem F . I think it uses Nlogn memory which is within the limits. What am I missing here ?
PS. I made a typo in binary search in the get() function as typing (a<<step) instead of (1<<step) but i have no idea why did that cause MLE.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Problem E: My code works till 7th test case and then shows long long int overflow in diagonistics --

"signed integer overflow: 58062342303970488 * 835 " says the error message,

but in my code it must not happen because

pdt=((pdt%MOD)*(NCR(val+y-1,y-1)%MOD))%MOD;

I have already taken mod before multiplication!

My submission : 32953649

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E can be solved using pure Segment Tree with complexity O((m+n)log(n)). First, run Eulerian ordering (using DFS) on this root tree. After that we got an array 2n elements where 2 adjacent elements have depth difference <= 1. We'll build segment tree base on this array. Each node [l, r] we store array of length r-l+1. Each i-th element of this array is minimum value which has depth <= i. Sorry for poor explanation. Sound like crazy but I got accepted submission. Pls check it out if you curious. 74651014

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can pls anyone tell me whats wrong with my code for rumors?

Your code here...
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define f(i,a,b) for(i=a;i<b;i++)
int main()
{
    ll i,m,n,ans=0,ele1,ele2;
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>m;
    vector<ll> gold(n+1);
    f(i,1,n+1)
    cin>>gold[i];
    vector<ll> a(n+1,0);
    for(i=0;i<m;i++)
    {
        cin>>ele1>>ele2;
        if(a[ele1]==0&&a[ele2]==0)
        {
            ans+=min(gold[ele1],gold[ele2]);
            a[ele1]=a[ele2]=1;
        }
        if(a[ele1])
        a[ele2]=1;
        if(a[ele2])
        a[ele1]=1;
        }
    f(i,1,n+1)
    if(a[i]==0)
    ans+=gold[i];
    cout<<ans<<"\n";
 
}
→ Reply
  • »
    »
    2 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    sorry if i am late you are counting minimum gold coins for every relation that is wrong consider test case n=3,m=2 coins:6 1 5 friendships:{(2,1),(1,3)} now the answer according to your code is 6 but original answer is 1

    → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Alternate solution for F : Build a merge sort tree on the euler tour of the given rooted tree, with list sorted by height, giving prefix minimum of assigned id's. To speed up query in merge sort tree from Log^2(N) to Log(N), use fractional cascading. Solution works easily in less than 2 seconds.

→ Reply