Problem: For a tree with n vertices. Every vertex has a value in range [1, c]. We define d(u, v) is number of distinct vertices's value on simple path from u to v, and  . We have to calculate all sum(i), 1 ≤ i ≤ n.
. We have to calculate all sum(i), 1 ≤ i ≤ n.
Constraints: 1 ≤ n ≤ 100000, 1 ≤ c ≤ 300000.
Do you have any idea?











I have just came up with brute-force solution. I think we need math or some advance data structures
That problem is similar to this one: http://www.spoj.com/problems/COT2/
But COT2 you just have to anwser 1e5 queries, this problem you may have to anwser 1e10 queries.
1e10 queries ??? Really ???
not explicitly , but if we need pairwise distinct count then it is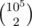
Can you post the link to the problem
I'm sorry, there is no link. This problem was on paper, and wasn't written by English.
I think we can solve this by centroid decomposition.
Start decomposing the tree. Say we have node R as our current centroid. Let T be the current tree. Let us now consider all paths in T that pass through R. Thus, after completely decomposing, all paths will be considered as they will pass thru some centroid R during the decomposition.
Do a dfs with R as root. For a node U in the ith subtree of R, let f(U) be the number of distinct colors from R to U . We now update sum(u) for paths that have the other endpoint in the first (i - 1) subtrees of R. Say we have cursum that stores the sum of no. of distinct colors for all paths from R to some node in the first (i - 1) subtrees of R. Also for each color C, we store curCount(C) as the no. of paths from R to some node in the first (i - 1) subtrees of R that contain the color C.
Update sum(u) + = (f(U) * #nodes - in - first - (i - 1) - subtrees) + cursum - sigma(curcount(C)). The summation is over the colors C which appear in the path from R to U. All the above calculation can be done in O(|T|). Hence overall complexity is O(NlogN)
Is there any solution for this problem without using centroid?
Thanks in advance