From few days, I have been thinking about a problem. But I can't figure out the solution.
Suppose you have an undirected graph having N nodes and M edges given. Given graph is initially a single connected component. Now the problem is, we have to delete a node of the graph such that remaining graph should be a single connected component. And this process should be repeated until the graph vanishes.
Now, we need to find the number of ways of doing it. Suppose graph is N = 6 and M = 7 as shown here
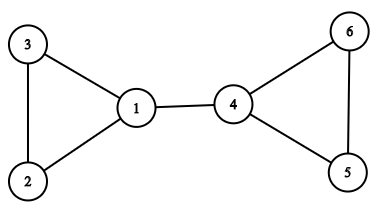
One way to delete the above graph is 2 — 3 — 5 — 6 — 1 — 4 (order of deleting the nodes).
Second way to delete the above graph is 2 — 3 — 5 — 6 — 4 — 1 (order of deleting the nodes).
Another way to delete the above graph is 2 — 5 — 6 — 3 — 1 — 4 (order of deleting the nodes).
Incorrect way of deleting the graph is 1 — 2 — 3 — 4 — 5 — 6 (Graph got disconnected after deleting node 1)
Can anybody help me with this question solution? Thanking all in advance.











I don't have a efficient approach but you can solve it recursively by finding each non articulation point in the graph and removing it and running the same function . I think the worst case is the complete graph where there are N! different ways to remove vertices
This will not work for more than 10 vertices graph(for ~2 sec TL).
Actually, I am expecting a DP or combinatorial solution to it if possible. And I think such solution should exist.