Here's the editorial. Hope you have a happy new year!
Code can be found here: https://www.dropbox.com/sh/i9cxj44tvv5pqvn/AACQs7LLNyTZT-Gt_AMf7UQFa?dl=0
Let's start off a bit more abstractly. We would like to know if the statement "if P then Q" is true, where P and Q are some statements (in this case, P is "card has vowel", and Q is "card has even number"). To do determine this, we need to flip over any cards which could be counter-examples (i.e. could make the statement false).
Let's look at the truth table for if P then Q (see here: http://www.math.hawaii.edu/~ramsey/Logic/IfThen.html). The statement is only false when Q is false and P is true. Thus, it suffices to flip cards when P is true or Q is false.
To solve this problem, we need to print the count of vowels and odd digits in the string.
First solve: ksun48 at 00:01:01
Breakdown of results for submissions that passed pretests
OK 6427 (98.74%)
CHALLENGED 60 (0.92%)
WRONG_ANSWER 22 (0.34%)
TOTAL 6509
This problem is intended as an implementation problem. The bounds are small enough that a brute force works. We can iterate through all mapping of numbers to directions (i.e. using next permutation in C++ or doing some recursive DFS if there is no built in next permutation in your language), and simulate the robot's movements. We have to be careful that if the robot ever gets in an invalid state, we break out early and say the mapping is invalid.
First solve: jonathanirvings, dotorya at 00:05:16
Breakdown of results for submissions that passed pretests
OK 4192 (83.72%)
WRONG_ANSWER 652 (13.02%)
CHALLENGED 126 (2.52%)
RUNTIME_ERROR 33 (0.66%)
TIME_LIMIT_EXCEEDED 4 (0.08%)
TOTAL 5007
This is another simulation problem with some geometry. As we push a disk, we can iterate through all previous disks and see if their x-coordinates are ≤ 2r. If so, then that means these two circles can possibly touch.
If they do, we can compute the difference of heights between these two circles using pythagorean theorem. In particular, we want to know the change in y coordinate between the two touching circles. We know the hypotenuse (it is 2r since the circles are touching), and the change in x-coordinate is given, so the change in y coordinate is equal to 
, where dx is the change in x-coordinate.
We can then take the maximum over all of these cases to get our final y-coordinate, since this is where this disk will first stop. Overall, this takes O(n2) time.
First solve: ehnryx at 00:04:05
Breakdown of results for submissions that passed pretests
OK 2694 (63.81%)
WRONG_ANSWER 1064 (25.20%)
CHALLENGED 448 (10.61%)
RUNTIME_ERROR 11 (0.26%)
TIME_LIMIT_EXCEEDED 4 (0.09%)
MEMORY_LIMIT_EXCEEDED 1 (0.02%)
TOTAL 4222
The main trickiness of this problem is that the sequence could potentially get arbitrary long, but we want an exact answer. In particular, it helps to think about how to reduce this problem to figuring out what state we need to maintain from a prefix of the sequence we've built in order to simulate our algorithm correctly. This suggests a dynamic programming approach.
For our dp state, we need to keep track of something in our prefix. First, the most obvious candidate is we need to keep track of the number of times 'ab' occurs in the prefix (this is so we know when to stop). However, using only this is not enough, as we can't distinguish between the sequences 'ab' and 'abaaaa'. So, this suggests we also need to keep track of the number of 'a's.
Let dp[i][j] be the expected answer given that there are i subsequences of the form 'a' in the prefix and j subsequences of the form 'ab' in the prefix.
Then, we have something like dp[i][j] = (pa * dp[i + 1][j] + pb * dp[i][i + j]) / (pa + pb). The first term in this sum comes from adding another 'a' to our sequence, and the second comes from adding a 'b' to our sequence. We also have dp[i][j] = j if j ≥ k as a base case. The answer should be dp[0][0].
However, if we run this as is, we'll notice there are still some issues. One is that i can get arbitrarily large here, as we can keep adding 'a's indefinitely. Instead, we can modify our base case to when i + j ≥ k. In this case, the next time we get a 'b', we will stop, so we can find a closed form for this scenario. The second is that any 'b's that we get before any occurrences of 'a' can essentially be ignored. To fix this, we can adjust our answer to be dp[1][0].
First solve: dotorya at 00:16:46
Breakdown of results for submissions that passed pretests
OK 449 (99.78%)
WRONG_ANSWER 1 (0.22%)
TOTAL 450
Let's ignore T for now, and try to characterize good sets S.
For every bit position i, consider the bitwise AND of all elements of S which have the i-th bit on (note, there is at least one element in S which has the i-th bit on, since we can always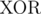 
by m). We can see that this is equivalent to the smallest element of S that contains the i-th bit. Denote the resulting number as f(i).
We can notice that this forms a partition of the bit positions, based on the final element that we get. In particular, there can't be a scenario where there is two positions x, y with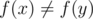 
such that 
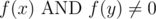. To show this, let 
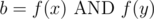, and without loss of generality, let's assume 
(it can't be simultaneously equal to f(x), f(y) since 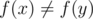). If the x-th bit in b is on, we get a contradiction, since b is a smaller element than f(x) that contains the x-th bit. If the x-th bit in b is off, then, 
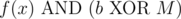is a smaller element of S that contains the x-th bit.
So, we can guess at this point that good sets S correspond to partitions of {1, 2, ..., m} one to one.
Given a partition, we can construct a valid good set as follows. We can observe that a good set S must be closed under bitwise OR also. To prove this, for any two elements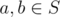 
, 
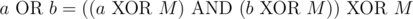. Since the latter is some composition of XORs and ANDs, it it also in S. So, given a partition, we can take all unions of some subset of the partitions to get S.
For an actual solution, partitions can be computed with bell numbers, which is an O(m2) dp (see this: http://mathworld.wolfram.com/BellNumber.html ).
Now, back to T, we can see that this decides some partitions beforehand. In particular, for each bit position, we can make a n-bit mask denoting what its value is in each of the n given values. The partitions are based on what these masks are. We can find what the sizes of these splits are, then multiply the ways to partition each individual split together to get the answer.
First solve: Petr at 00:26:54
Breakdown of results for submissions that passed pretests
OK 166 (100.00%)
TOTAL 166
Let's make a few simplifying observations
- It is not optimal to connect a red and blue point directly: Neither Roy or Biv will see this edge.
- If we have a sequence like red green red (or similarly blue green blue), it is not optimal to connect the outer two red nodes. We can replace the outer edge with two edges that have the same weight. This replacement will form some cycle in the red-green points, so we can remove one of these edges for a cheaper cost.
With these two observations, we can construct a solution as follows. First, split the points by the green points. Each section is now independent. There are then two cases, the outer green points are not directly connected, in which case, we must connect all the red/blue points in the line (for 2 * length of segment weight), or the outer green points are directly connected, in which case, we can omit the heaviest red and blue segment (for 3 * length of segment — heaviest red — heaviest blue). Thus, this problem can be solved in linear time.
Be careful about the case with no green points.
First solve: Petr at 00:38:32
Breakdown of results for submissions that passed pretests
OK 246 (90.44%)
WRONG_ANSWER 24 (8.82%)
RUNTIME_ERROR 2 (0.74%)
TOTAL 272
This is a digit dp problem. Let's try to solve the subproblem "How many ways can the i-th digit be at least j?". Let's fix j, and solve this with dp. We have a dp state dp[a][b][c] = number of ways given we've considered the first a digits of X, we need b more occurrences of digits at least j, and c is a boolean saying whether or not we are strictly less than X or not yet.
For a fixed digit, we can compute this dp table in O(n2) time, and then compute the answers to our subproblem for each i (i.e. by varying b in our table).
First solve: dotorya at 00:49:58
Breakdown of results for submissions that passed pretests
OK 46 (100.00%)
TOTAL 46
First, let's find connected components using only AND edges. If there are any XOR edges between two nodes in the same component, the answer is -1.
Now, we can place all components in a line. However, it may be optimal to merge some components together. It only makes sense to merge components of size 2 or more, of which there are at most k = n / 2 of them.
We can make a new graph with these k components. Two components have an edge if all of the edges between them are OR edges, otherwise, there is no edge.
We want to know what is the minimum number of cliques needed to cover all the nodes in this graph. To solve this, we can precompute which subsets of nodes forms a clique and put this into some array. Then, we can use the fast walsh hadamard transform to multiply this array onto itself until the element 2k - 1 is nonzero. Naively, this is O(2k * k2), but we can save a factor of k by noticing we only need to compute the last element, and we don't need to re-transform our input array at each iteration.
First solve: dotorya at 01:49:01
Breakdown of results for submissions that passed pretests
OK 10 (100.00%)
TOTAL 10
kudos to a lightening fast editorial!
Is there any way to interpret E as a vector space or group or something like that?
If I'm not mistaken, E should be related to counting the number of topologies on {1, 2, ..., m} in which the given family of n sets is open.
(Not topologies but sigma algebras — lapsus calami)
It is not a requirement in topological spaces that the complement of an open set is also open (In fact, in spaces like R^n, the complement of an open set is a closed set, and only R^n and the empty set are both open and closed sets). So in this problem, what is asked is exactly to count the number of topological spaces on
, such that the complement of any open set is also an open set.
Such spaces happen to also be linear subspaces of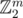
, since it is easy to write xor using only and, or and not. This observation might or might not help in arriving at the key observation on partitions (it is equivalent to observing than, when performing a careful Gaussian elimination, one can achieve a triangular matrix that has exactly one "1" per column).
Continuing with this completely unnecessary abstract translation, the key observation regarding partitions is equivalent to the fact that the Kolmogorov quotient of our space has the discrete topology (Kolmogorov quotient "glues" indistinguishable elements into one new single element).
I think the term you are looking for is "Sigma Algebra".
Indeed! Nice catch. So the key observation can also be stated as "finite sigma algebras are essentially equivalent to partitions". Googling that right now shows a related question here: https://math.stackexchange.com/questions/143796/number-of-sigma-algebra-on-the-finite-set
Which is how I solved it :D
Well, I would have probably figured it out on my own if I had thought about it for a minute or two, but it was too tempting to just google "Number of sigma algebras on a finite set".
In fact (to be even more pedantic :D) you don't need the "sigma" part, which refers to countable unions.
Since everything is finite it is just an algebra of sets.
For anyone delighted with the present display of pedantry, a friend of mine just made me notice that finite topologies are equivalent to preorders (a point x is less than another y, if any open set containing y also contains x), which are also essentially just "transitive" directed graphs.
So in the finite case:
Sigma algebra --> partitions
Topology --> preorder
maths too hard~~
Codeforces is becoming awesome day by day :D
Editorial even before system testing finished, amazing punctuality grandmaster.
My solution to H is probably equivalent to yours, but it's explained in much simpler terms than Walsh-Hadamard transform :)
See "4.2 Inclusion-exclusion" in http://www.wisdom.weizmann.ac.il/~dinuri/courses/11-BoundaryPNP/L01.pdf
Nice solution. I noticed my solution looked like inclusion/exclusion but didn't know how to explain it. I found it easier to explain through walsh hadamard transform since that's how I originally thought of the problem/solution. Glad to know there is a simpler explanation :)
I actually admire that your knowledge enables you to use Walsh-Hadamard transform in a solution so easily :) I had to Google the paper to make progress.
Thanks a lot for the contest!
The O(nk·2.45n) algorithm (dynamic programming, only iterating over maximal independent subsets) also passes in less than 1 second.
Unfortunately, too many bugs :(
We can also all borrow a trick from dotorya:
That should probably fail on a chain of length 23, though?... Or does it have so many attempts that it passes that one as well?
For a chain of length 23, I think the expected round is at most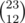
.
I have no time left and implemented a similar solution.
And I passed all the system testcases with only 100 iterations and 15ms :)
At least for a bipartite graph, this solution should work in O(2n).
Take one valid coloring, and suppose that there are B black vertices and W white vertices. If dotorya chooses a permutation such that all black vertices come before all white vertices (and vice versa), it works correctly. This happens with probability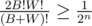
.
Is this O(2n) for general graphs or not?
What about complement of complete tripartite graph (so? Growth rate of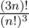
is around O(33n).
UPD: I misunderstood algorithm, sorry for many updates.
However, it seems like it might be more difficult to bound this runtime.
Doesn't it always handle complete tripartite graphs correctly?
What do you think about the graph on n vertices where vertex i is connected to vertices in interval [i - k, i + k] with chromatic number k + 1?
Actually I didn't compute probability at all. I just wrote general time-cutting method and prayed this would pass. Sorry :( After the conteat, I thought that the worst case is a chain with 23 vertices, which makes 10^-6 probability, which can pass this within time limit. But I was not sure whether this is the worst case...
There's nothing to be sorry about, I meant it when I said we should borrow a trick from you — you got the problem accepted quicker, and that is good!
I imagine that the number of k-colourings can get quite big though (n! for a complete graph, and I'm not sure if that's the worst case). I see you used a randomly selected prime modulus to get a solution that is right with high probability (and which is hack-resistant), but would a solution that's guaranteed correct (presumably using bignums) run fast enough?
Well, the probability of error is at most 23*1e-9, so I would say that there's not much difference — i.e., in my mind it's like quicksort working in O(nlogn).
But I don't know a deterministic fast enough version of my solution.
I managed to add an extra O(logk) factor, and I had to use modulo 232 hash to fit into TL. Luckily it passes.
Really nice problems! I kept thinking about how to handle the infinitely large case in D, but couldn't figure it out at last :( And also, F is a really cool problem I think :D
WOW! Thank you so much for super fast Editorial and also for the awesome problems !
Whoohh such a fast editorial!!!!!!!!
F was a Div2C question. I wonder why the authors kept it at F :(
Use the spoiler tag to share code or put your submission link, please.
next_permutation STL function only permutes according to the lexicographically greater comparator...hence in our case, it does consider all the 24 cases needed.
can anyone please help in understanding the dp transition in D.
goodbye rating
dude you solved 4 question on one go. you shouldn't be saying this :P
but the problem D had cost most of my time during the contest. :( Anyway the problems are good, yet I'm foolish.
Problems blew my mind, great contest-great problems.
For C, do we need to compute
dyfor all discs that can possibly touch (i.e. all discs in the≤ 2rrange), or can we just compute it for the disc with the highestycoordinate of these?You want to find the highest y+dy overall, not the highest y (and then + the dy of that).
My question is:
Suppose a disc X is within the +/-
2rrange. That means, if the disc currently being processed keeps dropping, it will eventually touch this disc X, unless it first touches some disc Z.The question is whether we can conclude such disc Z must have a higher Y coordinate than disc X.
I.E. for N discs in the range, the dropping disc must touch the one with the highest Y coordinate.
No, that's not true in general. You can try this case for example:
For the last disk, the highest y-coordinate disk wihtin range is the fourth one, but it will touch the second disk first.
No, that's false. if the highest-y disc is far away, and an almost-as-high-y disc is very close, it can touch the almost-as-high disc before the highest disc.
For concreteness, consider R=2, discs at (0, 2), (2, 1), and a new disc dropping at x=2. Then it will touch the (2,1) disc first.
That is where I fell :( I found the highest y colliding with a circle and then found the dy of that. :/
Great question btw!
Light-speed Tutorial,Light-speed System Test! I like it!
Editorial before Final testing. So fast. (y)
Editorials before system testing. That's a perfect goodbye to 2017 (*-*)
Great problems and a fast, nice, and concise editorial. Great Job!
There is a slight formatting error with the bell number link. (Extra right bracket at the end)
Thanks for good contest!
In Problem D Can somebody please explain why infinite length sequence is not necessary for "exact answer" ?
Didn't solve it, but I'm guessing it's because you can find the expected value of the amount of trials until first success with a closed form formula: https://www.cut-the-knot.org/Probability/LengthToFirstSuccess.shtml
Just 1/p.
At some point adding only one 'b' will satisfy the condition k. The probability of adding n 'a's then one 'b' at this point is: (1 - p)n × p where p is the probability of putting a 'b' (e.g: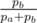
).
Hence the expected value of the sequence's length is: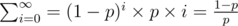
which is finite.
I know i am wrong,but i don't know why
why cant i say that
E = (1 — p)(E + 1) + p
because it has probability p of ending here,taking one step,or it has 1 — p of continuing,which takes one extra step
then
E = E(1 — p) + 1 — p + p
E * p = 1
E = 1 / p LE:this would give me the average number of steps untill i stop,but i should subtract 1 from it because i am interested in the average numbers of ab,not the avreage length. So 1/p — 1 = (1-p) / p
This is correct!!
yeah but i didn't realise for a long time that i need to subtract 1 :))).
But yeah,now it's corect :))
can you please help me in understanding the solution. I didn't understand : "because it has probability p of ending here,taking one step,or it has 1 — p of continuing,which takes one extra step" please elaborate it a little and if possible please explain it with an example.
So lets say 2 events could happen:
-a succes with probability of p
-a failure with probabilty of 1 — p we are at the first step,and we ant to see the expected number of steps untill the first succes
well if you have a succes(with probability p),then you only take one step. so E = p * 1 + the other case
if you have a failure(with probability 1 — p),then imagine that the next step is exactly like step 1,so the expected from that point would be the same. But,because you already had a failure,you must add one to it.
so E = p * 1 + (1 — p) * (E + 1)
if you do a bit of math this means
E = 1 / p
Now,back to our original problem,this is the expected length of a string untill we put a b.this would give us length — 1 more ab's.
So the real expected value is E — 1 = (1 / p) — 1 = (1 — p) / p
here p is probability to get 'ab' ?
no,p is probability to put b
so pb/(pa + pb)
I wonder how to prove this formula..
proof — https://imagebin.ca/v/3mS1m1CZVCff
Thanks
Why we need to use DP if the answer to the problem is
(1-p)/p? I can not understand it at all.The condition for applying the formula is when adding only one ‘b’ is enough to satisfy the condition ‘k’. This means that we have constructed a prefix of ‘a’s and ‘b’s, and that appending one ‘b’ to our prefix is enough to satisfy our condition.
To construct that prefix we use DP. The formula is applied when we hit a base case.
For problem D, I managed to get the formula but then I did not know how to make sure P and Q to be coprime. It turned out that I did not have to do anything and it would still pass. Can someone explain to me please why. (I used the same formula in the editorial)
Say you have integers p = p'g and q = q'g where g = gcd(p, q).
Then pq - 1 = p'g(q'g) - 1 = p'gg - 1q' - 1 = p'q' - 1.
Makes sense, thanks.
What is wrong with my approach to problem C ? Approach — for any circle- check all the points in the range c-r to c+r (c is center). find which previous circle(if any) in that range has the largest height. so it will touch that circle. then find the height as per the formula in the editorial. and update the range with the new circle.
My solution link http://mirror.codeforces.com/contest/908/submission/33786083
I haven't seen ur code but you have to check from c-r-r to c+r+r
why is it? range of the outermost points of the circle colliding should be [c-r,c+r] right?
The center of the circle it collides with is another r distance away
I think you made a mistake that I hacked a few other solutions on too: you've assumed that the disk you hit first will be the one that stopped with greatest y, but that's not necessarily true if there is one with a slightly lower y but much closer x.
Will there be an editorial in Russian?
You can use Chrome and then translate automaticaly all the page
It should be noted for problem F that, if there are no green points, you do not have to connect the red points and the blue points. In every other case, the optimal solution must involve connecting all points to each other, but, in this case, none of the red points have to be connected to the blue points. The problem may be a little misleading in this regard, as it says that Roy and Biv want all the points to be connected; however, later on, it does specify that they only want all the points they can see to be connected.
In H, I've picked random number and calculated result modulo this number, hopeing, that when number of colorings will be greater than zero, then it will also after moduling be greater than zero. Can you prove, that we don't have to use any modulo (so use 2^64), and it'll still be ok?
Thanks for the contest :) was really fun ^^ and thank you for the fast editorial! srsly.
And wow kudos for the solution in multiple language!!
what is wrong in my solution for problem C the link is here.
Figured out :D Thanx for the comment bmerry
Editorial has appear faster than ratings. Hm....
I can't get D solution. Could somebody explain the solution with more detail?
Finally I've got it! solution coded directly from formula 33810491
What is wrong with this solution for Problem C http://mirror.codeforces.com/contest/908/submission/33779874 . It is giving WA for Test Case 7.
Got it.
Why is the formula for D not dp[i][j] = (pa * dp[i minus 1][j] + pb * dp[i][i minus j]) / (pa + pb) ?
As in to reach current state with i a's we can only arrive here from having i-1 a's
and to reach current state having j ab subsequences we can add b to prefix with i-j a's and get a prefix with j ab's
Thanks :)
EDIT(for those who clicked pluses): Okay, so it seems we are working backwards, because our base cases are when j >= k, it means that at (i,j) we are ending our algorithm, so expected value of 'ab' subsequences is j.
Because of that our answer should be dp[0][0]
we also have the i + j >= k condition, to ensure that a's in our prefix doesn't exceed b's so that out count of a's are bounded by k.
Therefore our answer is dp[1][0], because there has to be atleast one 'a' to form some amount of 'ab' subsequences
Thank you your comment helped to understand the way the editorial thinks.
The key is that you start the algorithm from a fixed state and it only matters the amount of a's and ab's sub-sequences to compute the expected ab's when the algorithm finishes
dotorya solved G at 00:49:58 before bmerry
Oops, thanks for catching this.
Didn't understand some moments in explanation of problem F. Firstly, outer points = the leftmost and the rightmost points on the line ? Assuming that let's consider the first case:
the outer green points are not directly connected, in which case, we must connect all the red/blue points in the line. Okay, look at the test:Firstly, doing the second observation I should connect 3 — 5 and 5 — 7. Okay, what's next? I guess I should connect 7 — 9 and 1 — 3 ? Just can't see something like that in editorial. Secondly, let's consider the second case:
the outer green points are directly connected, in which case, we can omit the heaviest red and blue segment. Word "directly" seems very strange to me there. I really can't imagine that case not counting variant when we have only two adjacent green points. For example:Are x = 1 and x = 5 points directly connected if they linked through the point with x = 3 ? Need more detailed explanation, please.
I think you may be misinterpreting what the observations give you. The main point is that there can be no edge that "skips" a green point, thus, we can split the problem into sections which are each independent so that we only need to solve the case where the only green points could be first and last points.
For the second case, I should have clarified that a "red" edge is an edge that connects (red/green) to (red/green), and a "blue" edge is an edge that connects (blue/green) to (blue/green).
In D why "The second is that any 'b's that we get before any occurrences of 'a' can essentially be ignored. To fix this, we can adjust our answer to be dp[1][0]."
Why just ignore it? Why doesn't it change the answer?
Those b's can't be part of any subsequence that forms 'ab', since there's no 'a' before them, and we're only interested in expected amount of times 'ab' occurs.
So what happens with sequences like "bab.." or "bbbaab.."? Don't we count them in the answer?
The reasoning is this way. With no loss of generality every case we run the algorithm start with a finite amount of b's and then an a. In all the cases so we finish with 1 a and 0 ab's, thus, by definition the answer is dp[1][0].
In problem D, I didn't understand the meaning of this statement.
You stop once there are at least k subsequences that form 'ab'.We can have infinite
bs then anab, can this be the case?Please help me understand the problem.
The second is that any 'b's that we get before any occurrences of 'a' can essentially be ignored.Shouldn't we multiply by 1 + p + p2 + .. where p = pb / (pa + pb) instead of ignoring?
dp[i][j] = (pa * dp[i + 1][j] + pb * dp[i][i + j]) / (pa + pb)When i = j = 0,
dp[0][0] = (pa * dp[1][0] + pb * dp[0][ 0]) / (pa + pb)bring pb/(pa+pb) to the left and it becomes (1-pb)/(pa+pb) = pa/(pa+pb) which cancels on both sides, so we get
dp[0][0] = dp[1][0]Ah, or continuing from what I said, the answer is (1 + p + p2 + ...) * pa / (pa + pb) * dp[1][0] = dp[1][0]. In either your derivation or what I wrote above, the initial 'b's cannot be "ignored", they simply cancel out with the leading a. Is there any intuitive explanation of this fact, or is lewin's editorial misleading in using the word "ignored"?
The number of 'ab' subsequences in a string s is the same as if there was an extra 'b' in the beginning of s (or two b's, three, etc).
Maybe it gets intuitive if you think that the distribution is constant for every "pattern" (I mean, s, s and an extra 'b', two extra b's, etc), and the expected value of a constant distribution is the value of the constant. It's like you could just get the value for s rather than the "average" of all these cases, since all their values are equal.
Logically, (pa+pb)/pa * dp[0][0] is the answer. Which is also equivalent to dp[1][0] by calculation. But how are they equivalent intuitively?
When will the ratings be updated ?
In solution code of D- why have you kept
? if we already have this check -
? First one will never be encountered.
Keep this if (ab >= k) condition above second one so that it is checked earlier
But its useless. if you have ab>=k then a+ab>=k is already satisfied. so it never executes.
Yes we can avoid that
Problem G can be solved in O(102n).
Well what do
oneandcntmean in your code? Would you please explain it a little bit? Thanks a lot.For fixed d, we would like to add o(x) = 111...1 (x's ones) to the answer if the number contains x digits not less than d.
To maintain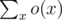
when we find a new digits not less than d, 
.
Got it. Thanks. But what does
means? Is it a typo?
My approach to F(New Year and Rainbow Roads) is to connect all green points where the
cost = (last green - first green). And then considering all green points a single one, connect it with the red ones using mst and do the same with blue ones. If there is no green point then ans should be(last red - first red + last blue - first blue). Can someone tell me where I am wrong...pleaseThe issue is that green points don't need to be directly connected: it is also valid to connect two green points using two different paths, one going over all the red points in between and one going over all blue points in between. It is easy to verify that this satisfies the constraints of the problem.
The following should be a breaking case that tests this case:
The correct answer for this case is 12, but it seems like your solution would output 14.
Understood..Thanks a lot!!
Can someone help where I am going wrong in finding closed-form condition for Problem D
Image
UPD : The derivation is actually correct we can put (1-a)=b then cancel out b and the ans will finally be x+b/a = done+f+(b/a)
https://imagebin.ca/v/3mS1m1CZVCff You mean this?
Yes, it is similar but i is varying from 0 to inf but I wonder what about that constant factor x(=done + f) Why it is not added later?
I think you are having trouble with the base case.
The formula you wrote there in the image is wrong. You are not considering all the cases. (a+ab >= k) is just the marker. here we know one b has to come to satisfy the min k ab's constraint.
In base case we have to consider three things -
expectation(of already present ab) it will simply 1*ab = ab
expectation(ab's formed with already present a's and coming one b) it will be equal to 1*a = a
expectation(of ab's formed with, one coming b and number of a's it brings with it).
For the calculation of 3. we consider say it brings 0 a or 1 a with it or 2 a or n a, upto inf a's. we consider all these cases by the summation formula in my image. As 1 and 2 will always be the same irrespective of the number of a's the coming one b brings with it.
summation formula =
Here if the coming number of extra ab's formed will be equal to number of a's it brings with it.
So, P(ab) = Pa*Pb and E(ab) = P(ab)*1 ,as 1 ab is formed
P(aab) = Pa2*Pb and E(ab) = P(aab)*2 ,as 2 ab's are formed.
similary you can compute upto inf and get the summation formula to generalize.
Here, Pa = a/(a+b) , Pb = b/(a+b) , Pa = 1 — Pb
Thanks :) Got it!
Can someone please provide a good explanation of problem E?
In problem D, in second base case, i + j ≥ k, can some one explain the closed form of expectation?
Check http://mirror.codeforces.com/blog/entry/56713?#comment-404349 and the image I posted in that thread above.
Nevermind, got it!
I will try to explain it:
i => number of a's in the prefix,
j => number of ab's in the prefix.
and i+j >= K,
so we can do like this:
1) put 1 b in the end => number of ab is now (i+j) which is >= K so we stop and probability is (Pb/(Pa+Pb)) so we add (i+j)*(Pb/(Pa+Pb)) .
2) put 1 a and then 1 b in the end => number of ab is now (i+j+1) which is >= K , so we stop and probability is (Pa/(Pa+Pb))*(Pb/(Pa+Pb)) so we add (i+j+1)*(Pa/(Pa+Pb))*(Pb/(Pa+Pb)).
3)put 2 a and then 1 b in the end => number of ab is now (i+j+2) which is >= K , so we stop and probability is ((Pa/(Pa+Pb))^2)*(Pb/(Pa+Pb)) so we add (i+j+2)*((Pa/(Pa+Pb))^2)*(Pb/(Pa+Pb)).
and so on..
Now if we add these it becomes =>
(i+j)*(Pb/(Pa+Pb)) + (i+j+1)*(Pa/(Pa+Pb))*Pb/(Pa+Pb)) + (i+j+2)*((Pa/(Pa+Pb))^2)*(Pb/(Pa+Pb)) + ...
Let's leave as an exercise for you to solve this. Spoiler: answer is => i+j+Pa/Pb
Hope this helps :)
Thanks, I got it from the picture and comment described in http://mirror.codeforces.com/blog/entry/56713?#comment-404349
i have a question for i+j>=k if i=k and j=0 is this like aaaaaa(k times) and 0 'ab' if we put 1 'b' at the end it become aaaaa(k times)b why we can stop this if we only get one 'ab' but not at least k 'ab'?
Can anyone explain paragraph 5th of D'solution? I couldn't get it's idea
see http://mirror.codeforces.com/blog/entry/56713?#comment-404349
This is how i understand: we consider all satisfied subsequence, for each of them, calculate p = probality and x = number of 'ab' sequence, then our excepted number equal sum of product of all pair (p, x). So why can we ignore subsequences which is large or have 'b' continuously at the beginning?
we are not ignoring the large subsequences. we are including that in the summation formula. also if you have b's in the beginning then number of ab's formed is zero since no a's are prior to those b's. so expectation = (probab of those b)*0 = 0, so we ignore that case.
I was wrong when asking
ignore subsequences which have 'b' continuously at the beginning. i mean why can we ignore all continuously 'b' at the beginning of every sequence, as the editorial said that we can ignore them, or did i misunderstood the editorial?For example, probality of adding 'a' is 0.3, adding 'b' is 0.7, then for subsequence 'bab', p = 0.147 and x = 1. But if we ignore first 'b', we get p = 0,21, which change the anwser.
Oh you are confused over the word "ignored"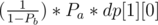
= dp[1][0]
our answer has to be Pbn * Pa * dp[1][0] for lets say n b's occurred before the first a.
so generalizing this case for we can get 0 to inf number of b's before first a.
we get ans = (Pb0 + Pb1 + Pb2 + ..) * Pa * dp[1][0]
=
I don't know why they didn't explain in the editorial like what you did. Ignore few explanations could make the editorial harder, when they can add them easily.
Maybe because It was div1+div2 combined that's why.
Yeah, but at least D is still for div 2
Also, intuitively you can think that if you start the algorithm from beginning in all cases you will expect to have n b's and one a in some moment, thus the expected answer in all cases is dp[1][0], thus ans=dp[1][0] no matter how we weigh the cases.
Looking at number of solutions passed each task we could notice that A,B,C and too far from D,E,F. I think difficulty should reduce more.. gradually.
Can't Understand G. Anyone?
In Problem E, can someone explain me — by taking f(i) as a partitioning factor how can we get a partition of the bit positions?
Elements with the same f value will belong in the same set in a particular partition.
Problem D.
-Let dp[i][j] be the expected answer given that there are i subsequences of the form 'a' in the prefix and j subsequences of the form 'ab' in the prefix.
-The answer should be dp[0][0].
These two statements seem contradicting to me.
We are working backwards. We start our dp from known values which are dp[i][j] where i + j >= k, and the answer is in dp[1][0]. In state dp[i][j] we can add a letter 'a' with probability p and have expected value which is in dp[i + 1][j] or 'b' with probability (1 — p) and have expected value from dp[i][i + j].
You start with an empty string (that does not have any 'a' nor 'ab' occurrence)
I think what may be troubling you is that the "base case" of this dynamic programming approach is not in the beginning, but in the end. (Sometimes the base case is i == 0 or j == 0, but here we have i+j >= k)
Ok, I got it now.
But still I think the definition of dp in the editorial is quite confusing. I suppose it would be more clear if explained as "answer we get if we start with a sequence containing i subsequences of the form 'a' and j of the form 'ab'". But maybe that's just my dullness.
Didn't know cards can have same indentity, which pay me 1 hack!
I have a solution to G with higher time complexity and I don't know how to make it better.
Supposed X have len digit, we enumerate the first different digit i with X (notice the case that the first element is 0) , then we can use any number in the last len-i digit. It can be solved with f[a][b],g[a][b] which means we have filled the first b digit using 0~a,the sum and the count of it(Remember to consider the number we filled in fist i-1 digit).
I have to pay len*10 in the part of enumerate , and used len^2*10 in dp , so the general time complexity is len^3*100 that can't pass the test cases :(
Can anyone help me?
My English isn't good and I may have many mistakes in my expreesion , sorry for it.
in problem E, can someone explain to me what is the relation between: 1- when f(x) != f(y) therefore f(x) & f(y) will be 0. and 2- the good sets S correspond to the partitions of {1,2,...,m} ??
Elements with the same f value belong in the same set in a particular partition
I think I'm missing some concepts in order to fully understand problem D. Can anyone point me out where to look?
In the first example, if we stop when we get the first 'ab' sub-sequence, how is it possible for expected value of the number of such sub-sequences be greater than 1 in the end?
Thank you.
For the first example, we could make a sequence like "aaab", which has 3 occurences of the subsequence "ab".
Ah, that's what message was about. Are these three exactly: "a**b", "*a*b" and "**ab"?
Anyway, I think I've got it now. Thanks :)
Can someone give a brief description on solution of D. I read the editorial, but couldn't understand it....
Define dp[i][j] as they expected answer of se start problem algoritm with Amy position that has i a's and j ab's subsequences. Imagine you start the algorithm from one of these positions. In one case worth pa a's are incremented and in the other case worth pb ab's are incremented by i. So we know in both cases the new state thus the expected answer in them (asumming we have already computed dp with higher i,j) We just make a weigthed average of expected answer in both cases to reach dp[i][j] formula (case a worths pa, expected answer dp[i+1][j], case b worths pb, expected answer dp[i][i+j]. (See Wikipedia for weigthed average, it is an easy formula ) Base case and final case are very hard. Try to think them and ask if you are lost
thanks a lot..... i understood it a bit now. One query, why the final answer is dp[1][0] and not dp[0][0]??
dp[0][0] is defines as any starting position with only b's. dp[1][0] is any starting positions with a finite amount of b's and then an a. It can be proved mathematically dp[0][0]=dp[1][0] but I used intuitive aproach. When you start algorithm you have 0 b's thus expected answer must be dp[0][0]. However no matter your luck when you the algorithm in all scenarios you end in a moment with a finite amount of b's and an a (could be 0 b's). Thus in all cases expected answer should be dp[1][0]
okay... understood it now.. thanks
Hi! and Happy new Year to all. In problem E, I think to understand the editorial (most of it) but I don't get how all hypothesis claimed there implies a solution for the given problem. If someone would give me an example where this hypothesis are used. thanks
Can anyone please explain Problem G in details ? Codeforces editorial was a bit difficult to understand. Something about dynamic programming on digits...... I watched Endagorion's screencast of the same, but I couldn't understand properly.
for those who are having problem in understanding D : https://discuss.codechef.com/questions/120548/help-in-understanding-expectation
All the credits to John_smith :)
Thanks, E(aaa)=E(aaaa)/2+E(aaab)/2 nice example explanation for understanding dp
yaah it's awesome ! ALl thanks to JOHN :)
btw did you have any good tutorial for centroid decomposition? If you have then please share!
Happy coding :)
Need some help for problem E. I understood it as letting fi=fj or fi*fj=0 for all i,j, thus counting the number of ways of partitioning {1,2...m}. But how are we take into account set T?
so, basically, T is describing whether 2 elements can stay in the same set in the partition or not.
for example, you are given T as (the same format as problem input):
And for example, you are now checking whether element 0 and 2 can be in the same set, then you retrieve their bits (just take the corresponding columns of the input matrix):
now the third row is 1 and 0, meaning if 0 is taken, don't take 2 in the final partition.
you will see that 2 elements can be in the same set iff their bits (columns) are the same.
So you can group the elements with same bits together and calculate how many ways you can partition them.
Thank you for the great problems and quality editorials!
Since I still have difficulty in understanding editorial of problem D, can I add one more question? Can you explain how i+j >= k can contribute to make sequence space closed ? For example, with k = 3, there are infinite i, j pairs. (3,0), (4, 0), (5, 0), and so on.
So for i + j >= k, if you get another 'b', you will stop. Now ignore the i and j.
Suppose you get a 'b' with probability
peach time, which corresponds topb/(pa+pb)in the problem. Then the expected number of experiments you have to do to get a 'b' is1/p.So i + j >= k the case where you can calculate the exact expected number.
Let me answer my previous question as I understood.
If i + j >= k, E(i, j) = i + j + Pa/Pb <== faceless_man showed how it is calculated. Though infinite i/j pairs satisfies i+j>=k, we want to have smaller number of base cases for the efficiency (which means smaller DP states to be calculated.)
So, with k=3, (3,0), (2,1), (1, 2) are considered as the base cases, but (4,0), (2,2), (3,1), (1,3) are not.
That D has to be one of the coolest DP problems I've seen. Seriously, compressing an infinitely long memoization matrix into finite size is sweet.
I can't get G solution.Can somebody explain me the solution with more details?
You need to calculate this subproblem: solve n[i][j], which means the number of integers that is <= X and when sorted, has i-th digit >= j. (say, i starting from 0 and counting from the least significant digit)
For example, let X = 22, and let's sort the numbers:
You will see that, n[1][1] = 10 {11,12,...,19, 12} and n[1][2] = 1 {22}.
Suppose you have this subproblem solved, you can get the final answer by doing sum for i to be the length of the sequence and for j to be 1 to 9:
i.e. you reformulate the sum of the original problem, by doing it digit by digit.
However, to calculate n[i][j] is not easy (I'm not sure). (this is similar to calculating bell numbers directly is not easy, you need a O(n^2) dp).
So, you now turn to calculate dp[a][b][c] for a fixed digit j. The state represents that you have considered
adigits, how many intergers <= X, when not sorted, have equal to or more thanboccurrence of j, given that integer is still equal to X or not (c). (the same defined in the official solution)After solving that dp, n[i][j] = dp[0][i + 1][0]. (Since you have a number >= j on i-th index, then you must have at least i+1 digits that are >= j for that number)
And to calculate dp[a][b][c], you will need: dp[a+1][b/b-1][0/1]. The boundary cases are when b = 0/ a = |len(X)|.
Also, you must be careful about the multiplication and modulo.
So you see this problem is not so direct. If this is your first-ish digit dp problem, don't worry. It is not easy to understand and you may want to first do some easier digit dp first. Also, you may notice that there is a common strategy for solving dp[a][b][c] (like, assuming whether you are getting a number
< or ==the given upperbound or so...).Can someone read my solution of problem H and tell me the complexity? http://mirror.codeforces.com/contest/908/submission/33975786
Can somebody explain me, how in problem D do we get 370000006 from 341/100 and 1e9+7? ... как взять дробь по модулю целого числа?
a / b = a * b^-1 ≡(mod m) a * b^-1 * b^φ(m) = a * b^(φ(m) - 1)
For prime m latter is equal to a * b^(m - 2). It can be calculated using binary exponentiation.
φ is called Euler function, b^-1 ≡(mod m) b^(φ(m) - 1) is called modular (multiplicative) inverse.
What is the meaning of "the expected number of times 'ab' is a subsequence in the resulting sequence" in D?