Блог пользователя mapvr3

solving (a/b) mod m

Автор mapvr3, история, 7 лет назад, По-английски 
(a/b) (mod P) = (a * b^-1) (mod P) = (a (mod P) * b^-1 (mod P)) (mod P).

Now, by Fermat's theorem, b-1 (mod P) will be b^P-2 (mod P). Of course, for this b and P must be co-prime to each other and P must be a prime. So, (a/b) (mod P) = (a (mod P) * b^P-2 (mod P)) (mod P). works only if P is prime and a,b are coprime to P

  • Проголосовать: нравится
  • -7
  • Проголосовать: не нравится

»
7 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

If P prime you can use fermat Dont depend on a,b. Also you can use fucntion of the Euler. a/b mod P = a * b^(f(P)) mod P. f — Euler fucn. For prime num f(p)=p-2.

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

You can also use extended euclid if a and P are coprime. Here's the equation a'x + b'y = gcd(a', b'), put a' = b and b' = P, since gcd(a, P) = 1, taking modulo both sides you have x as your answer.

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится +6 Проголосовать: не нравится

If b | a, then we can do some thing like: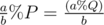 , Where Q = P * b.

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    I think your idea is quite wonderful. I have met a problem asking, for instance, to calculate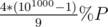 , and I think your idea can solve this sort of problem very well.

    Perhaps it is even not necessary for P to be a prime integer under this condition.

    → Ответить
  • »
    »
    6 лет назад, # ^ |
      Проголосовать: нравится -6 Проголосовать: не нравится

    Great Idea! In a problem, I was told to find (1 + a2 + a3 + ... + ab - 1)modN .It seems I can now use the Geometric Sum Formula.

    → Ответить
»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

What should i do when p is not prime And a,b are not co-prime to p?

→ Ответить
  • »
    »
    6 лет назад, # ^ |
    ← Rev. 6   Проголосовать: нравится 0 Проголосовать: не нравится

    Let's talk about the question when p is prime but a, b are not co-prime to p factorize the power of $$$p$$$ from $$$a (a_p)$$$ and $$$b (b_p)$$$

    the answer is $$$\frac{a}{p^{a_p}} \div \frac{b}{p^{b_p}} \times p^{a_p-b_p}$$$

    in this case $$$\frac{a}{p^{a_p}}$$$ and $$$\frac{b}{p^{b_p}}$$$ are both coprime. Therefore, there won't be any problem calculating the modular inverse

    However this approach is basically useless unless $$$a$$$ is within 64-bit integer range.

    One special usage of this is extended lucas theorem

    Now, lets talk about scenarios when p is not a prime

    We know that $$$p$$$ can be expressed as the product of prime powers

    $$$p = P_1^{C_1} P_2^{C_2} ... P_K^{C_K}$$$

    after that we can solve each $$$P_i$$$ using the above method and merge the result using Chinese remainder theorem.

    → Ответить