BumbleBee's blog

Number of digits in the binary representation of an integer
By BumbleBee, history, 7 years ago, In English

I usually find the number of digit in the binary representation of an integer in the following way:

int digit = 1 + (int)log2(n);

I used to think that this way is absolutely correct as I never found any error. But today I got WA in problem number B (Codeforces Round 456) due to finding the number of digits in this way and I understood that this way isn't 100% correct. An integer n = 288230376151711743 was given in the case in which I got WA verdict.

While testing the error, I printed the 2 base log of 288230376151711743 using the log2() function of C++ and it printed 58. According to that 2^58 should be equal to 288230376151711743, but it isn't. 2^58 is equal to 288230376151711744.

So I guess, the value of log2(288230376151711743) is 57.99999999... or something like that which is very close to 58 and due to precision issues log2() function returns 58 in this case.

To avoid such errors I changed the way of finding the number of digits in binary in the following way:

int digit = 1 + (int)log2(n);
long long int x=(long long int)pow(2,d-1);
if(x>n) d--;

After changing my code in this way I got AC verdict, but I am still not sure about the accuracy of my way.

I want to know how much accurate is this way of finding the number of digits. If it is still not accurate, kindly suggest some other ways of finding the number of digits in the binary form of an integer which are accurate and efficient enough.

  • Vote: I like it
  • -2
  • Vote: I do not like it

Comments Comments (21)
| Write comment?
»
7 years ago, # |
  Vote: I like it +11 Vote: I do not like it

log2/pow and these functions use doubles so precision might be bad. Don't use them in these cases.

If you want to know how many 1's are number in base 2, then just iterate on each bit individually, and check if it's 1.

For example for (int i = 0 ; i < 62 ; ++i ) if((number) & (1LL << i)) ++ones;

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    For counting ones, it might be faster to use the "fenwick tree" method where you remove the lowest set bit each time: 

    int ones = 0;
while(x){
    x -= x & - x;
    ++ones;
}

    I ran a quick test comparing the two methods, and it seems as though fenwick runs faster on a large number of random test cases:

    code

    Edit: __builtin_popcountll(x) is faster than either of the two methods, so use that instead.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can this way give any error?

      int digit = 1 + (int)log2(n);
long long int x=(long long int)pow(2,d-1);
if(x>n) d--;
      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I also had thesame error in java with the following code

long num = 1L << (int) Math.ceil(Math.log(n)/ Math.log(2));
if (num > n) num >>= 1;
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In Java, you can simply use

    int len = Integer.toBinaryString(x).length();

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Integer.numberOfTrailingZeroes(Integer.highestOneBit(x)) + 1

      → Reply
»
7 years ago, # |
  Vote: I like it +13 Vote: I do not like it

With gcc you can compute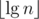 using

__builtin_clzll(1ll) - __builtin_clzll(n)

which should get compiled to use the bsrinstruction, so it's really fast.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Does it give the accurate value of log2(288230376151711743)?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      The argument gets passed as an unsigned long long, so no precision is lost and the answer will be correct for any positive 64-bit integer. (n=0 is UB or unspecified as far as I remember.)

      PS: To compute the number of ones in the base 2 representation, use

      __builtin_popcountll(n)
      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    The main problem is not about speed its about precision, As the OP stated

    lg(288230376151711743) is slightly smaller than 58,

    lg(288230376151711743+1) is exactly 58.

    The result of the first after floor should be 57, but due to precision its returned as 58.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      __builtin_clzll works with integer type, there's no precision error

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Also, you could use std::__lg(n) for cleaner code.

    → Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

I usually use

Time complexity : O(log n)

while(n>0)
 {
    n/=2;
    cnt++;
 }

cnt is the number of bits

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

A GCC specific solution is to use __builtin_clz() function. It gives you the number of leading zeroes in the binary representation of a number. So, if you subtract it from 32 (number of bits in an int), you get what you want. For long long, you need to use 64 — __builtin_clzll().

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks. It works. What is the complexity?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It's complexity is O(log N), same as that of log2(), but if you check the implementation, the number of cycles __builtin_clzll() takes is much lesser. I just ran them both for 10^8 numbers. log2() took 2.6 seconds while __builtin_clzll() took 0.4 seconds.

      Moreover, __builtin_clzll() returns an int so you won't have any precision issues

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yes. I tested it too. I ran both functions on a vector of 10^6 long long integers. __builtin_clzll() was more efficient.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

When I started learning algorithm (5 months ago), I was lazy that time and keep searching for functions that help me to do things faster (such as pow and log) but one day, I got some bugs with the function pow and log, the result could not be exactly, so I decided to use my own. Here is the code that I'm using, with the function logarit, you can modify it tho, the function power runs in fast time ( O(log)).

long long power(long long a, long long n)
{
    if (n == 0) return 1;
    long long t = power(a, n / 2);
    if (n % 2 == 0) return t * t;
    else return t * t * a;
}

long long logarit(long long n)
{
    long long x = 62;
    while (power(2, x) > n) x --;
    return x;
}
→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

I had the exact same problem, and I solved it casting the parameter as a long double

like so

int digit = 1 + (int)log2((long double)n)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I tried with this and it is still not accurate. It is still showing 58 when I print this:

    (int)log2((long double)288230376151711743)
    → Reply