Hello, This is a problem from dhaka regional'15
problem link: Honey King
In short, in a different kind of 2D plane you are given some points(10^5 maximum) in the plane. find the minimum hexagon such that all points lie inside the hexagon.
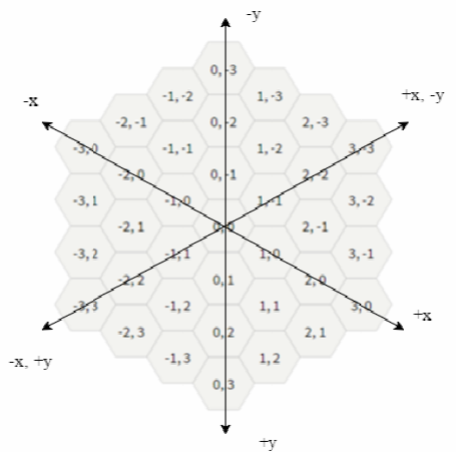
So for a cell (x, y), there are six surrounding cells, up(x, y − 1), down(x, y + 1), up_left(x − 1, y), down_right(x + 1, y), up_right(x + 1, y − 1) and down_left(x − 1, y + 1). For points (0, 0), (−1, 0) and (−2, 2), This is the hexagon witch includes minimum number of inner hexagons. Output the minimum number of inner hexagons. so 7 is the answer in this case.
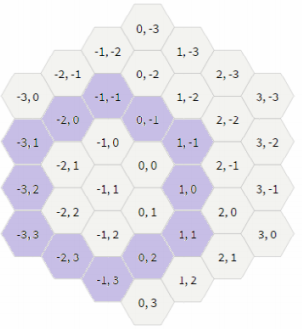
Please give me some hints.










Seems like too hard for me to solve :(
Binary search the radius of hexagon and check whether it's large enough.
There're at most 6 important points.
The one with max of x, min of x, max of y, min of y, max of x+y, and min of x+y.
When fixed a radius and fixed the x coordinate of the hexagon, the possible range of the y coordinate can be computed with the help of those 6 points.
The number of possible x coordinate is only O(104)
What do you mean by important points? can't understand it
Using Binary search to find the length of a side of hexagon.
Then you can calculate the number of inner hexagons using the formula:
num = L*(L+1)*3+1
here is my code: code (may help...)