Note that the number of hacks is palindromic!
Tutorial is loading...
Code: 35036267
Tutorial is loading...
Code: 35036334
Code (bless pragmas): 35036420
Tutorial is loading...
Code: 35036537
Tutorial is loading...
Code: 35053688
Tutorial is loading...
Code (backward dp): 35036591
Code (forward dp): 35036674
Tutorial is loading...
Note that the solutions might not fully match the editorial, though the ideas are still the same.
Code (GreenGrape): 35055945, 35055961
Code (KAN): 35055995
Code (xen): 35055977










Thanks for the pretty early editorial!!!
In solution for problem E you wrote that time complexity is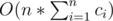 . Can you explain why ? Because for every n we are doing
. Can you explain why ? Because for every n we are doing 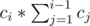 operations so I think it's more like
operations so I think it's more like 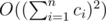
It was possible to solve this problem faster — we can use standard trick and write ci using O(logci) nominals. Than complexity is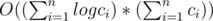 .
.
Instead we can use two pointers
Here To achieve previous complexity.
What do you mean by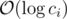 nominals?
nominals?
Say c = 2n + k, where k < 2n. Then, these 2 are equivalent: choosing an element [0...c] times and choosing subsets of {20, 21...2n - 1, k + 1} where an element of subset is the number of times we choose the element.
So then we can compute the maximum value of min(dp[i—1][k] + X, W + k * B) + cost[i] * k, where k takes ci different values by splitting the interval into O(logci) intervals and taking max from each?
Isn't that slower than the solution using a queue?
Saw your submission — 35045018, got the idea. Thanks :)
Can you suggest a problem where this ideia is necessary?
It's indeed as you said, but we can achieve the previously said complexity:
We have dp[i][j] = max(dp[i][j], min(dp[i — 1][j — k] + X, W + (j — k) * B) — cost[i] * k). Let's get a new k = j — old k. Now, dp[i][j] = max(dp[i][j], min(dp[i — 1][k] + X, W + (k) * B) + cost[i] * (k — j)). We can take -cost[i] * j from inside to get
dp[i][j] = -cost[i] * j + max(dp[i][j], min(dp[i — 1][k] + X, W + (k) * B) + cost[i] * k)
Now we can use a Max_queue (push element, pop element as in a queue but answers what's the max inside the queue) to solve it in O(n * sum(birds)). Edit: since nothing inside the max/min depends on j
Code: http://mirror.codeforces.com/contest/922/submission/35036545
how to write the Mathematical formula like above?
read about LaTex formulas. On codeforces they must be in $$ signs.
example: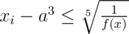
x_i - a^{3} \le \sqrt[5]{ \frac{1}{f(x)} }I learned it from this blog: http://mirror.codeforces.com/blog/entry/20729.
For 922B - Magic Forest it is possible to write a bruteforce solution and just calculate answer for all possible input dynamically (O(n^3) with no optimisation). And then use pre-calculated answers in final submission.
No, it's not possible, it will be tle because n is too large for O(n^3) to fit in a 1s time limit.
It's even possible to pass with O(N^3) without compiler optimisation. http://mirror.codeforces.com/contest/922/submission/35010602
I think your code is optimised because c < a+b
for (c = b; c <= n && c < a + b; c++)Yeah I mean, it's not a "compiler" optimisation (pragma) unlike the editorial, and is still an O(N^3) algorithm.
Very good contest ! The problems were all short and I enjoyed solving it immensely !
editorial of problem D is not available. How to solve Problem D.
Briefly: it is not hard to proof that cnts and cnth in (s[i] + s[j]) and in (s[j] + s[i]) equals. So answer will depend only on their relative location.
We can sort all si with any n·logn sort algorithm, using
ans(s[i] + s[j]) > ans(s[j] + s[i])as compare function.Then build string t from sorted array s1, s2, ..., sn and output ans(t).
http://mirror.codeforces.com/contest/922/submission/35039116
In C,my brute force solution passes. i can't understand why,can anyone explain??
I think it means that condition
m[n % i] == 1becomes true at small k (why? theory of numbers/modules and etc.), else you stop iterating and output "Yes".When I did not read that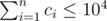 in D and for an hour was trying to find the way to calculate dp for 107 birds :D
in D and for an hour was trying to find the way to calculate dp for 107 birds :D
There were so many hacks in problem A that I've thought this will be a regular unrated contest)))
Why? 99% author planned (and waited) many hacks in A.
What is an official solution for problem F?
What about the editorial of problem F? I want to know how to solve it, thank you!
I think this tournament was a good tournament! The problem was neat and fun. I have a question in Problem C I know that K is always above 43, but I do not know why. When K is 6t, 6t + 1, 6t + 2, 6t + 3, 6t + 4, we prove it all, but when K is 6t + 5, we can not prove it. Please help me! Please!
What's wrong with the solution of the editorial? Have you read it?
If there are no repeated remainders in
n % 1,n % 2, ...,n % 43, then it has to be the case thatn % 1 = 0,n % 2 = 1,n % 3 = 2, ...,n % 43 = 42. This is equivalent to1 | n + 1,2 | n + 1, ...,43 | n + 1. Therefore alsoLCM(1, 2, ..., 43) | n + 1, so9419588158802421600 | n + 1. Therefore this is only possible ifn >= 9419588158802421599.Thank you! I think my thinking was short on this part. Thank you so kindly.
Can someone explain me why in Magic Forest we have to include conditionals like x < j and i+j <= x (x = i ^ j) I understand why there's x > n but I can't figure out meaning of other conditionals.
x < j: in that case the third number is smaller than the second, which is not allowed. The statement say that we have to count tripples (a, b, c) with a ≤ b ≤ c.i + j < x: if this is the case than we don't have a triangle. E.g. try to draw a triangle with the side lengths 1, 1, and 3. Impossible. For more information: Existance of a triangeCould anyone tell, in question "C", how does complexity O(min(k,log(n)) is calculated? Is that an approximation(to achieve >43) or can we calculate maximum number through LCM in O(log(number)).
Look up the sequence of lcm of first n integers on the Internet. (> 43) then lcm > 10^18.
I solved 922C in O(1) time. Although, the solution in the editorial seems straight forward, it didn't strike me during the contest! Solution link here.
Your gcd function doesn't work in constant time so it is O(log n)
Can anyone please briefly explain the claim em - k < = C.m1 / 3 that is made in the editorial for problem F.
Number of divisors of n is approximately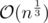
Possibly a dumb question but how do we show that? It's a cool fact but I'd liek to understand it better.
See Growth Rate
Thanks
m is the least number such that e(m) >= k. so e(m-1) < k. between m and m-1 you removed edges of divisors of m. so e(m)-number of divisors of m < k, so e(m)-k < number of divisors of m. and number of divisors of m has (approximately) an upper bound of m^(1/3)
I got it now. Thank You everyone.
My solution drops out all i (starting from 2) if cntpairs(i) ≤ currentpairs - k.
I'm not sure if it is correct solution but it got AC: http://mirror.codeforces.com/contest/922/submission/35051349
my idea is like yours, but i'm not sure too, do u kown the reason now? can u tell me?
I've found that a lot of people pass the problem but they don't know why it works.
Can any one provide the topdown dp solution for problem E?
It's just a knapsack problem
Can someone elaborate C? I don't get how k is approximated to 43?
Explanation
My AC solution to F: http://mirror.codeforces.com/contest/922/submission/35125488
First I find the least m where e(m) >= k (like in the editorial). then I see how many edges should be removed to reach k, let their name be "excess". I followed a greedy approach where: while excess != 0, I remove the node from the interval [floor(m/2)+1, m] which has the greatest number of divisors and this number of divisors is <= excess, then subtract this number from excess. I know that the initial value of excess is O(m^(1/3)), but why does this greedy approach always succeed ?
For the cases where the number of primes in the interval [floor(m/2)+1, m] is >= excess it succeeds because the primes will always make it possible to reach k. but for the 16 possible counters mentioned in the editorial, why does this approach succeed ?
For Problem F, " You could've even written recursive bruteforce " is mentioned in the editorial. What would be the time complexity for the same ?
can someone please explain why (n % i = i-1 : for all valid i) implies (n+1) % i = 0!
Explanation
thanks for this :)
My solution 35116450 for Problem F uses the idea in GreenGrape's 35055945 solution with only difference in that I did upper_bound over all numbers (not only over primes) and surprisingly it got AC. Fortunately it happened after the contest, to be fair with others. Seems like the acceptance criteria is much less intimidating than the problem statement looks.
What is wrong in my solution for D
http://mirror.codeforces.com/contest/922/submission/35161046
Please help
I think this is the opposite of what you wanted to do? If c1 equals to 0, that means there are no 's', so it should go to the end of the final string.
For example, the answer of 2 sh h
should be 2 with the string "shh", but your code make it "hsh" so it prints 1 instead.
Also, the answer could exceed the range of int, like in case of you have 50000 's' first then 50000 'h', which makes the answer 2.5 billion.
Can E be done recursively?
If the knapsack problem can be recursion, then it can also, obviously this is a knapsack problem
If you're talking about a memory search, of course
how are u relating it with knapsack?
can u please tell in detail?
Let us solve this problem step by step.
First, take the bird as an item, the number of birds is the amount of this item,the bag volume in this problem is not necessary to defined accurately, for your convenienc,you can take the sum(c) as the bag volume :D
In this problem, the choice of birds is in a certain order.“Moving only forward",but in the knapsack,we actually consider each item in the order we specify.
right? So it doesn't affect us to solve this problem.
Now, this problem turns into a multiple knapsack problem(I don't know the exact English name of this problem,but i think u can understand it , right?)
Let's study how to solve this simple problem before adding other conditions,one of the ways is to dismantling the same items into different items (but their volume is the same, in this problem each bird's volume is 1,value is -cost[i]).
The problem becomes a common knapsack problem.
For instance,you have You have 6 A items and 4 B items,You can think of them as 10 things, but some things are the same volume and same value.
By the way,The best way to split it is this:
for example , you have 16 A items you can dismantle them into 1,2,4,8,1(2 ^ n ). You just have to think about the 5 pieces that are split up.
Next, it's time to solve the problem completely.
mana capacity indicates that the current backpack value cannot exceed this upper limit,and after putting the bird in the backpack, the value of the knapsack cannot be negative (mana exhausted).You need to solve the maximum volume of knapsack that can be filled up under this restriction( Of course, it can't exceed the total number of birds, that is sum (c).)
my english not very well , if u cant understand,you can see my code http://mirror.codeforces.com/contest/922/submission/35191705
Of course, in fact, just dp[maxc] is enough,A bit of redundancy in this code
It's not recursively, and if you need it, I can write a code to show u
Maybe some details I forgot to answer
Thnx alot,it really helped..
I accept the problem F just now, but i still don't kown why i can accept. first i find the min m satisfy e(m) >= k, then i choose the prime from 2 to m, Obviously, if I delete a prime number, it will reduce the M / P pair. If I delete the prime number, the total pair is still larger than k, and I'll delete it。
here is my mainly code (I didn't do any other extra judgment as solution.)
i want to kown how to prove this idea is correct???
In addition, I want to know the details of the practice of recursion. Can anyone explain to me more about the principles and proof of F in more detail? I admit that I might be stupid: D
I have a randomized solution for F which differs from the editorial. The main idea is that if we have a set $$$S$$$, then adding an element $$$x$$$ to the set and recomputing $$$I(S)$$$ can be done quickly. So we can randomly insert an element if $$$I(S) < K$$$ and remove a random element if $$$I(S) \ge K$$$. A set data structure does not support querying a random element, so we can use priority based data structure instead to allow for random removal/increments.
141680253