I searched google , about this , I understand only that worst case happens when a,b are consecutive fibonacci numbers .
Someone says Euclidian algo's time complexity is O(log(a+b) ) , some says O(log(n) ) . But their explanation is not clear to me . I read the first answer from here : https://stackoverflow.com/questions/3980416/time-complexity-of-euclids-algorithm .
I pasted it bellow . It describes the analysis of euclid algo .
"One trick for analyzing the time complexity of Euclid's algorithm is to follow what happens over two iterations:
a', b' := a % b, b % (a % b)
Now a and b will both decrease, instead of only one, which makes the analysis easier. You can divide it into cases:
Tiny A: 2a <= b
Tiny B: 2b <= a
Small A: 2a > b but a < b
Small B: 2b > a but b < a
Equal: a == b
Now we'll show that every single case decreases the total a+b by at least a quarter:
Tiny A: b % (a % b) < a and 2a <= b, so b is decreased by at least half, so a+b decreased by at least 25%
Tiny B: a % b < b and 2b <= a, so a is decreased by at least half, so a+b decreased by at least 25%
Small A: b will become b-a, which is less than b/2, decreasing a+b by at least 25%.
Small B: a will become a-b, which is less than a/2, decreasing a+b by at least 25%.
Equal: a+b drops to 0, which is obviously decreasing a+b by at least 25%.
Therefore, by case analysis, every double-step decreases a+b by at least 25%. There's a maximum number of times this can happen before a+b is forced to drop below 1. The total number of steps (S) until we hit 0 must satisfy (4/3)^S <= A+B. Now just work it:
(4/3)^S <= A+B
S <= lg[4/3](A+B)
S is O(lg[4/3](A+B))
S is O(lg(A+B))
S is O(lg(A*B)) //because A*B asymptotically greater than A+B
S is O(lg(A)+lg(B))
//Input size N is lg(A) + lg(B)
S is O(N)
So the number of iterations is linear in the number of input digits. For numbers that fit into cpu registers, it's reasonable to model the iterations as taking constant time and pretend that the total running time of the gcd is linear.
Of course, if you're dealing with big integers, you must account for the fact that the modulus operations within each iteration don't have a constant cost. Roughly speaking, the total asymptotic runtime is going to be n^2 times a polylogarithmic factor. Something like n^2 lg(n) 2^O(log* n). The polylogarithmic factor can be avoided by instead using a binary gcd."
In the upper statement , I am unable to understand this line (4/3)^S <= A+B . How does it come from ? If anyone can explain please help .
If anyone has other easier explanation , please share .











You want to perform the operation remove 25% repeatedly. If you look at this operation carefully, you can realize that it can by accomplished by a multiplication of (because
(because  ).
).
Therefore you want to multiply by until it drops to 1, which gives
until it drops to 1, which gives 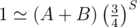 or
or 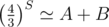 .
.
I am not clear another thing . That is
"Small A: b will become b-a, which is less than b/2, decreasing a+b by at least 25%." . How b will become b-a ?
For small A: a > b/2 but a < b .
If a means dividend and b means divisor in each step :first step :
b— — — — — — —a— — — — —asecond step:
a- — — — — — — -b— — — — — -b%a``b%a— — — — — —a— — — — — —a%(b%a)in the third step b=b%a , a=a . How this b value become equal to b-a ? [ in b-a , b and a are input numbers ]
Since (input a) > (input b)/2 but (input a) < (input b) . So result of (input b) % (input a) will be <=b/2 . But how it is equal to (input b)-(input a) ?
One question when you write equation , how do you create image like this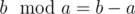 . Any tool ?
. Any tool ?
Codeforces supports Latex formulas: http://mirror.codeforces.com/blog/entry/20729
In (a+b) , if b is decreased by half then how (a+b) decreased by 25% ?
This should be pretty intuitive. But if you want a proof:
Initially we had the sum a + b. After the one operation we have the sum a + (b - a) = b. So the sum decreases by a.
How much is a in a + b?
So the sum actually decreases by more than 33.33%.
I do remember something like the worst case scenario is a pair of consecutive fibonacci numbers, and thus you get a complexity related to golden ratio