Overflow? You may need int128.

G:

tl;dr, compute how many 0 ≤ i < n, 0 ≤ j < m with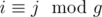 or 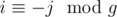where g is gcd of 2(n - 1) and 2(m - 1) using inclusion-exclusion principle.

First, let's get rid of grids and consider the point setting: a ray of direction (1, 1) shoots from the origin and reflects when hitting the boundary of [0, n - 1] × [0, m - 1] rectangle.

For a point (i, j) in the rectangle, it is passed by the ray if and only if there are integers a, b satisfying one of the four conditions:  ± i + 2a(n - 1) =  ± j + 2b(m - 1). This condition comes from that we can pave rectangles all over the plane and ignore ray reflection.

Above condition is equivalent to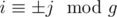 . Then by some elementary math skill and inclusion-exclusion principle we can calculate how many (i, j) satisfying the equation and get the answer.

There's a 1 line formula... Let me see if I can remember it. Let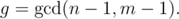 Then the answer is

You can find this by computing the number of times the bishop goes up and down the board (say $m < n$). This is going to be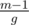 because the smallest integer k such that m - 1|k(n - 1) is 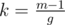. After that you count number of repeated squares, noting that a square can only be repeated twice or else you get a cycle.

Got presentation error on TC#38... Any ideas of getting such a verdict?

But I believe in my solution: 1) find how many times bishop needs to make a trip from one shortest side to opposite shortest side (it is: (min(N-1,M-1)) / gcd(N-1,M-1)), then multiply this count by length of this way (which is: max(N,M)), 2) subtract a number of intersections of ways, which is in a grid in a rectangle of ( max(N-1,M-1) + 1 ) x ( min(N-1,M-1) - 1 ), and a number of intersections is ( max(N-1,M-1) / gcd(N-1,M-1) + 1 ) x ( min(N-1,M-1) / gcd(N-1,M-1) - 1 ) / 2.

We used N^2 dp for N <= 500 and logn * C (C <= 10, maybe smaller) otherwise, which passes pretty easily, although it's more boring to code

Precalculate binomial coefficients bin[100][100] one time.

Process intervals using a recursive function, starting with intervals containing a single 1, and discarding all intervals with duplicate elements. You can check if an interval of size s is a permutation by checking if its maximal element is s. After checking that, also process the two intervals obtained by extending the interval to the left or to the right to include its mex (smallest missing element).

Let's find all intervals [L, R] such that

• K = R - L + 1 is at least two.
• A_L, ..., A_R is a permutation of 1, ..., K.
• K is to the right of 1 in the interval.

Try all N possibilities for R. For a fixed R, find the maximum i such that i ≤ R and a_i = 1. Clearly, K is the maximum of a_i, ..., a_R. Now we can uniquely determine L because L = R - K + 1. Use hashes to check if a_L, ..., a_R is a valid permutation.

It also proves that there are at most 3N good intervals.

Thanks. We also thought to make this "search" but didn't notice that there are not much good intervals.

Just binary search over the coordinate of the line. Once you've fixed it, the problem becomes: find the convex hull and calculate its area. BTW, how to solve D?

Assuming dp_mask is the number of placing elements from n - k + 1 to n, where k is equal to the number of 1's in the mask and 1's in the mask correspond to the occupied places by numbers from n - k + 1 to n, such that after performing m given operations of swapping these elements will be in their positions (it means that n will stand at n-th position, ..., n - k + 1 will stand at (n - k + 1)-th position after performing all swappings).

dp₀ = 1.

Then let's iterate over 0's bits in the mask and try to put there the value n - k (k is the number of 1's in the mask). It means we are processing (adding) elements from n to 1. Now we can check whether it's a correct mask or not. We know that the elements that are 1's in the mask are greater than n - k, and the elements that are 0's in the mask are less than n - k. Now we can construct sequence using number 0, 1, 2, where 0's stand on the positions, that are zero in the mask, 1 stands where we want to put n - k in the mask and 2's stand on the positions, where 1's in the mask. So we just sort this sequence applying given comparisons and if it's sorted in the end, we can do this transition.

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <deque>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>
#include <string>
#include <cmath>

typedef long long ll;
typedef long double ld;

using namespace std;

const int MAXN = 15;

ll dp[(1 << (MAXN + 1)) + 10];

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(0);
	//freopen("input.txt", "r", stdin);
	//freopen("output.txt", "w", stdout);
	
	int n, m;
	cin >> n >> m;

	vector<pair<int, int> > edges;
	for (int i = 0; i < m; i++) {
		int a, b;
		cin >> a >> b;
		--a;
		--b;
		edges.push_back({ a, b });
	}

	dp[0] = 1;
	for (int mask = 0; mask < (1 << n); mask++) {
		for (int i = 0; i < n; i++) {
			if (mask & (1 << i)) {
				continue;
			}
			vector<int> res;
			for (int j = 0; j < n; j++) {
				if (mask & (1 << j)) {
					res.push_back(2);
				}
				else if (i == j) {
					res.push_back(1);
				}
				else {
					res.push_back(0);
				}
			}
			for (auto &e : edges) {
				if (res[e.first] > res[e.second]) {
					swap(res[e.first], res[e.second]);
				}
			}
			bool ok = true;
			for (int j = 1; j < n; j++) {
				if (res[j - 1] > res[j]) {
					ok = false;
				}
			}
			if (ok) {
				dp[mask | (1 << i)] += dp[mask];
			}
		}
	}

	ll ans = 1;
	for (int i = 1; i <= n; i++) {
		ans *= i;
	}

	cout << ans - dp[(1 << n) - 1] << "\n";
	return 0;
}

We failed test 6 when we missed some initialization.

No idea what the test is, though it should be a fairly simple test, IMO.

First, pick a lexicographically minimal length-k substring, and remove all strings which have such as substring.

After that, you can append other length-k substring, possibly overlapping some. You should try to pick and append the substring to make it lexicographically minimal. (Note that length matters — in case of aabbbcc and aabbbccd, you should pick the former one, as it contains the latter one) After that, remove all strings which have such as substring.

The limit is kinda small, but you should pick a reasonably fast DS or efficient code. I used std::set to maintain the strings.