Hey CodeForces, recently I came accross a problem, finding an element in an array which occurs more than n/3 times, while using constant space and linear time. Now I admit, this is a well known interview problem and plenty of articles exist which cover this, however I have struggled to find one that offers proof of correctness or any explanation.
Please help me understand the correctness.
Basic Idea: Like we do in Boyer-Moore algorithm, however instead of keeping one element and counter, keep 2 , then update them similar to the original algorithm.
Thank you CodeForces!










You can have a randomized algorithm. That is -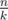 times. If you repeat this x times, then you have
times. If you repeat this x times, then you have 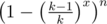 probability of hitting a number with frequency more than
probability of hitting a number with frequency more than 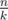 .
.
Take a random number from the array, and check if it appears more than
If n = 105 and k = 3, then if you check only 40 random numbers, you have 99% probability of hitting such a number.
It may have complexity O(nx) or O(n + x) depending on the bounds of the numbers of array, and linear space. However, this may not be fesible always if x needs to be high.
This idea can be used to solve this problem — 840D - Destiny
Do you have the prove of the probability?
Hint: Try finding the probability that you don't hit such number in all (x - 1) guesses.
Is it not important that you hit 40 distinct random numbers, in which case you will have to use auxillary memory to keep track of what you've already checked. Also can you prove how many calls to the rand() function you require to get 40 distinct values ?
Anyway, thank you for giving me a new problem solving method ! :)
You don't need to keep track of which numbers you have visited. The point is, if you keep taking a random number and check, you'll find one in around 40 checks. So, just keep trying untill you find one. If you are going to use C/C++, the
rand() % nshuold be enough. You may safely assume that it doesn't generate same number over and over again in close calls.But in case, if the data is generated based on the numbers generated by
rand(), then you can just reseed it by some random prime. Or userand() * 1ll * rand() % nor something like that.Makes much more sense now, thank you !
You can also have an array A, initialized to contain [1....N] and random_shuffle() it and then choose the first however many elements you need as indices.
Forgive me if I am wrong , but is it not more complex, I mean that will definitely take O(n) operations, but Rezwan's method is expected to take much fewer.
Anyway I was primarily looking for proof of correctness of the said algorithm.Since I primarily like understanding why algorithms are correct, even though I am not very good at it.
Solving problems is a different game, for ex, in this problem one could probably use quickselect on multiples of k and still get correct answer in expected O(kn)time, but that is not the point.
It's the same complexity
oh yeah.. my bad !
Problem: Find all elements of A, |A| = n, that appear more than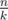 times.
times.
Let's split A in two smaller subproblems A1, |A1| = n1, and A2, |A2| = n2, such that n = n1 + n2. We can define Ki = (a1, a2, ..., ak) as the k greatest elements by frequency in subproblem Ai and F(x, Ai) as the frequency of element x in Ai.
Then we argue that the elements of K1 and K2 are the only candidates to appear more than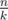 times in the original problem (K).
times in the original problem (K).
Let's do a proof by contradiction and assume that there is an element x such that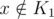 ,
, 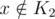 and
and 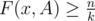 . We know that
. We know that 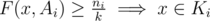 . Using the converse we know that
. Using the converse we know that 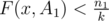 and
and 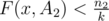 then:
then:
F(x, A) = F(x, A1) + F(x, A2)
So, the elements of K1 and K2 are the only candidates to appear more than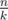 times in the original problem (K).
times in the original problem (K).
For a more formal proof, use strong induction on |A1| + |A2| within the induction on |A|. Regards.
Nevermind thought out a rough proof:
Consider k-1 stacks(for now, we will reduce to counters later) and the remaining array that is to be seen, now instead of incrementing the counter, imagine you push the same value of the element on the respective stack. similarly for decrementing, imagine you remove one element from every stack.
Now define solution set as elements in stack+ remaining array. we can remove elements from solution set only when it contains k distinct elements.. that is k-1 distinct elements in the stacks and a new element from the remaining array. so now we discard k distinct elements from the solution set.
After we are finished with the entire array, we would have discarded only tuples of k distinct elements. It is now very clear that elements with frequency greater(strictly) than n/k remain in the stack. If the array did not contain any greater-than-n/k-elements, the stack will have garbage values. Hence we need to check once more in (k-1)n time.
Instead of having stacks with same elements he compressed it into value+num_instances pairs.